Потенциальные кривые.

Зависимость потенциальной энергии от расстояния между взаимодействующими частицами называется потенциальной кривой. Знание потенциальной кривой позволяет делать определённые выводы о характере механического движения, не решая дифференциальных уравнений движения, что почти всегда сопряжено с большими трудностями.

В качестве примера рассмотрим одномерные движения частицы под действием консервативных сил. Пусть частица может двигаться только вдоль оси Ox. Из закона сохранения механической энергии (W=const) следует:

Так как , то движение частицы может происходить только в областях, где .

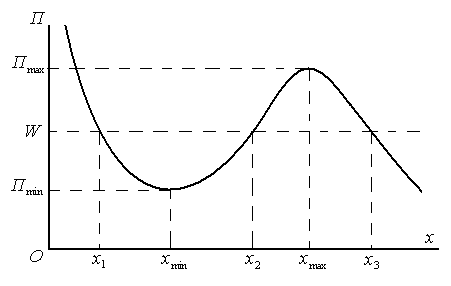Рассмотрим ситуацию, изображённую на рисунке.

Участки потенциальных кривых около минимумов потенциальной энергии называют «потенциальными ямами», а около максимумов потенциальной энергии «потенциальными барьерами». При значении механической энергии W, изображённой прямой параллельной оси Ox, в области «потенциальной ямы» движение ограничено координатами и и является финитным, в области справа от координаты движение не ограничено и является инфинитным.

В точках и сила, действующая на частицу равна нулю, т.е. эти точки соответствуют положению равновесия частицы. Положение равновесия с минимумом потенциальной энергии является устойчивым, так как при любом смещении частицы от этого положения возникает сила, возвращающая частицу к положению равновесия (сила направлена в сторону убыли потенциальной энергии).

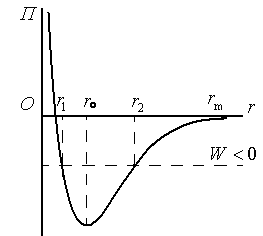Положение равновесия с максимумом потенциальной энергии, очевидно, будет неустойчивым. В потенциальных ямах частица совершает колебательные движения около положения устойчивого равновесия. При значениях «потенциальный барьер» непреодолим для классической частицы, т.е. область пространства с координатами недостижима для частицы.

В заключении рассмотрим два примера из области молекулярной физики и физики ядра.

Примером потенциальной кривой с потенциальной ямой является кривая взаимодействия молекул. Взаимодействие между молекулами зависит от их природы и расстояния между ними. Это взаимодействие носит сложный характер.

Качественная зависимость потенциальной энергии взаимодействия молекул от расстояния между ними представлена на рисунке. Отметим, что молекулярные взаимодействия проявляются на малых расстояниях порядка нескольких и быстро спадают до нуля, т.е. являются короткодействующими.

Как видно, при сближении молекул возникают силы притяжения, которые затем, переходят в силы отталкивания. Такой характер молекулярных взаимодействий объясняет существование конденсированного состояния вещества (жидкое и твёрдое) и особенности движения молекул в этих состояниях. В газах энергия молекул . Молекулы газа находятся в среднем на расстояниях - радиус действия молекулярных сил. Поэтому молекулы газа движутся как свободные частицы от одного столкновения до другого, которые можно считать упругими при не очень высоких температурах. Этим можно объяснить наблюдение свойств газов.

В жидкостях и твёрдых телах молекулы ведут «оседлый образ жизни», находясь приблизительно на расстояниях друг от друга, совершая колебательное движение около положения равновесия в пределах (см. рисунок). Механическая энергия молекул в конденсированном состоянии W<0. Физические свойства вещества определяются глубиной «потенциальной ямы» и средним значением механической энергии молекул <W>.

Примером потенциальных кривых с «потенциальным барьером» является потенциальная энергия частиц в ядре (см. рисунок). Ядерные взаимодействия являются короткодействующими. Радиус их действия порядка нескольких Ф (Ферми), 1Ф=.

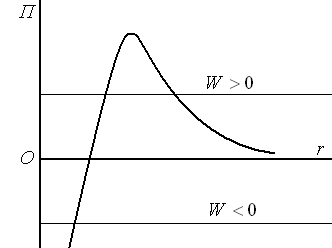При приближении заряженных частиц к ядру отталкивание переходит в притяжение. Но ядерные взаимодействия зависят не только от расстояния. Они являются настолько сложными, что не поддаются аналитическому описанию. В этой ситуации в ядерной физике используют энергетический подход.

Описание процессов распада и синтеза ядер связано с решением «барьерных» задач. Например, ядерная частица с энергией W<0 не может покинуть ядро. Частица с энергией W>0 с точки зрения классической механики также не может вылететь из ядра. Но квантовая частица может с некоторой вероятностью, которая зависит от высоты потенциального барьера и его ширины, может вылететь из ядра. Это явление называется «туннельным» эффектом. Оно связано с волновыми свойствами микро частиц. Отметим, что при этом закон сохранения энергии не нарушается.

Примечание. Понятие энергии является более фундаментальным, чем понятие силы. К примеру, в квантовой механике понятие силы лишено смысла, так как в квантовой механике состояние частицы задаётся иначе, чем в классической механике.

Энергия – это всеобщая скалярная мера движения материи, а закон сохранения энергии является фундаментальным законом природы, который не знает исключений. Его фундаментальность связана со свойством однородности времени и отражает свойство неуничтожимости движения материи.