Потенциальная энергия тяготения.
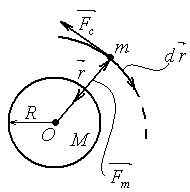Рассмотрим
систему тело + Земля в ИСО, связанной с
центром Земли, так как центр инерции
системы практически совпадает с центром
Земли. Тело движется под действием силы
тяжести
и силы сопротивления воздуха
.
Землю будем представлять однородным
шаром, а тело – материальной точкой.
Тело будет двигаться согласно основному
уравнению динамики:
.
Умножим левую и правую части скалярно
на элементарный перемещение
:
,
,
,
,
,
где
,
,
,
- элементарная работа диссипативной
силы:
Выражение в круглых скобках с точностью до постоянной
имеет размерность энергии
=Дж
и представляет собой механическую
энергию тело + Земля, где
является потенциальной энергией
гравитационного взаимодействия тела
с Землёй. Постоянная в выражении для
потенциальной энергии определяется
выбором нулевого значения потенциальной
энергии. Например, принимая П=0 при
,
постоянную следует принять равной нулю.
Систему тело + Земля можно считать
замкнутой, но неконсервативной, так как
на тело при движении действует
диссипативная сила, работа которой
.
Механическая энергия системы тело +
Земля убывает.
В идеальном случае, когда отсутствуют диссипативные силы или ими можно пренебречь, механическая энергия сохраняется:
,
,
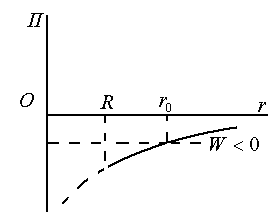Примером
такого движения является движение ИСЗ
и орбитальных космических станций. При
указанном выборе постоянной потенциальная
энергия тяготения отрицательна:
(см. рисунок).
Следовательно, механическая энергия
системы тело + Земля может принимать
отрицательные значения
,
если
.
При этом тело совершает финитное
движение, ограниченное радиусом Земли
и расстоянием
.
При
движение тела не ограничено справа,
т.е. при таком значении механической
энергии тело может преодолеть притяжение
Земли. Такие движения называются
инфинитными.
Минимальная скорость, при которой тело
преодолевает притяжение Земли, называется
второй космической скоростью. Оценим
эту скорость. Воспользуемся для этого
условием
:
Откуда
,
где
- первая космическая скорость,
Теорема о потенциальной энергии. Связь между консервативной силой и потенциальной энергией.
Обобщая два рассмотренных примера можно записать выражение для механической энергии консервативной системы частиц
,
где
- кинетическая энергия i-ой
частицы, П – потенциальная энергия
взаимодействия частиц системы.
Механическая энергия системы изменяется под действием внутренних диссипативных сил и внешних сил:
,
где
-
работа внутренних диссипативных сил,
- работа внешних сил.
В замкнутой и консервативной системе
(
,
)
механическая энергия сохраняется:
,
.
Из закона сохранения механической энергии и теоремы о кинетической энергии следует:
.
Положительная работа консервативных сил равна убыли потенциальной энергии системы. В этом суть теоремы о потенциальной энергии.
Важным следствием теоремы о потенциальной энергии является независимость работы консервативной силы от траектории и равенство нулю при движении по замкнутой траектории.
Используя теорему о потенциальной энергии
можно получить связь между консервативной силой и потенциальной энергией:
,
где математическая операция grad (градиент) преобразует скалярную функцию в векторную по следующему правилу:
.
Оператор grad обозначается
греческой буквой
(Набла):
Проекции силы на координатные оси соответственно равны:
,
,
.
Сила всегда направлена в сторону
максимальной убыли потенциальной
энергии и численно равна изменению
потенциальной энергии, приходящейся
на единицу длины в этом направлении
.
Зная выражение для потенциальной энергии, можно определить закон силы. Например, если потенциальная энергия является функцией одной переменной вида
,
где
- размерная постоянная,
-
действительное число. Выражение для
закона силы F(x)
получается простым дифференцированием
функции П(x):
.
В частном случае m=2 получается выражение для закона Гука, а при m=-1 – закон обратных квадратов.
Лекция 7.