Механическая энергия и её виды. Закон сохранения механической энергии.
Понятие работы. Кинетическая энергия.
Действие силы во времени характеризуется импульсом силы, что приводит к изменению импульса частицы (тела) – векторной меры механического движения:
.
Сила действует также в пространстве, так как точка приложения силы перемещается в пространстве. Действие силы в пространстве характеризуется работой. Скалярное произведение вектора силы на элементарный вектор перемещения называется элементарной работой и записывается в виде:
,
где символ «
»
означает, что элементарная работа в
общем случае не является полным
дифференциалом. Конечная работа силы
равна:
,
где интеграл берётся вдоль траектории
от положения
до положения
.
Работа измеряется в Дж (Джоуль) и является
скалярной величиной (
,
).
Преобразуем выражение для элементарной работы. Для этого воспользуемся основным законом динамики
,
,
где
.
Скалярное произведение
.
Следовательно
,
так как
Выражение
называют кинетической энергией частицы
(тела).
Действие силы в пространстве (работа) изменяет кинетическую энергию частицы (тела):
,
.
Это утверждение составляет содержание теоремы о кинетической энергии.
Ели на свободную частицу (тело) не
действует сила
,
то кинетическая энергия тела свободной
частицы сохраняется
.
Откуда следует, что кинетическая энергия,
как и импульс, является мерой
механического движения частицы
(тела). Кинетическая энергия является
скалярной мерой механического движения,
измеряется, как и работа, в Дж.
Импульс и кинетическая энергия в классической механике связаны соотношением:
Консервативные и неконсервативные силы.
Среди механических сил можно выделить консервативные и неконсервативные силы. Консервативные силы – это силы, которые зависят только от координат взаимодействующих частиц и не зависят от скорости их движения. К консервативным силам относятся, например, силы тяготения и упругие силы. Неконсервативные силы зависят от состояния движения частиц (тел). К неконсервативным силам относятся все силы трения и сила сопротивления.
Закон сохранения механической энергии.
В замкнутой и консервативной системе частиц сохраняется механическая энергия системы, равная сумме кинетических энергий частиц системы и потенциальной энергии взаимодействия частиц системы:
Потенциальная энергия системы – это статическая энергия системы.
Система частиц называется консервативной, если между частицами действуют только консервативные силы.
Рассмотрим частные случаи замкнутых систем. Найдём выражение потенциальной энергии для этих случаев и покажем, что механическая энергия сохраняется.
Потенциальная энергия упругих взаимодействий.
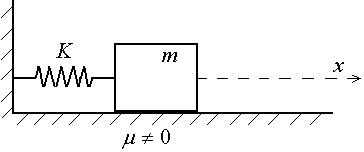Рассмотрим
систему состоящую из твёрдого тела и
идеальной упругой пружины (см. рисунок).
У идеальной пружины масса равна нулю.
Это физическая абстракция применяется
когда массой пружины можно пренебречь.
Тело движется вдоль оси X
под действием упругой силы и силы трения
согласно основному уравнению динамики:
,
где
равно смещению от состояния недеформированной
пружины.
Умножаем левую и правую части уравнения
на элементарное смещение
:
,
,
,
,
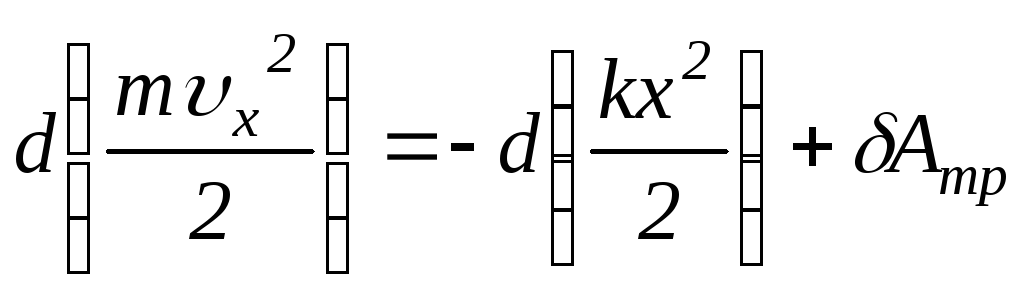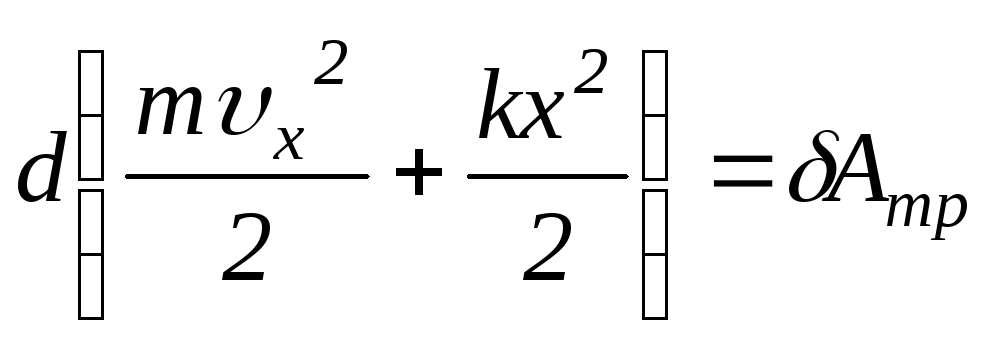где
,
,
,
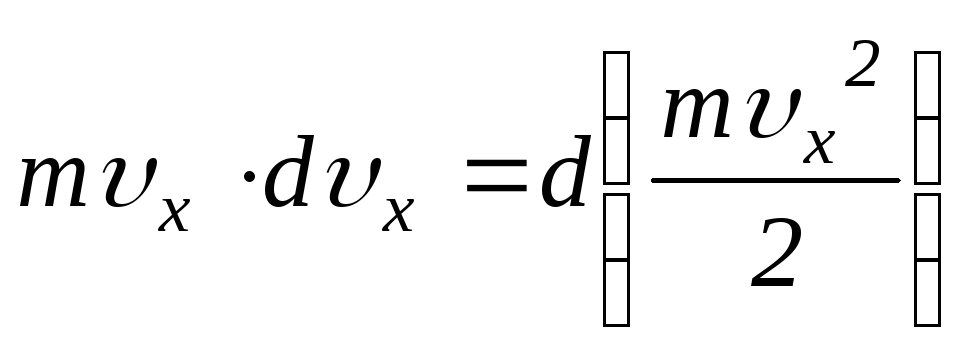- работа силы трения.
Получаем
,
где выражение
называется потенциальной энергией
деформированной пружины,
- кинетическая энергия тела.
Механическая энергия системы равна:
В рассмотренном примере изменение механической энергии замкнутой системы равно работе силы трения:
.
Так как
,
то
.
Механическая энергия замкнутой системы убывает под действием силы трения и, как показывает опыт, превращается в тепловую энергию. Это явление называется диссипацией. Неконсервативные силы также называют диссипативными.
Если в замкнутой системе действуют
только консервативные силы, т.е.
отсутствуют диссипативные силы, то
механическая энергия в такой замкнутой
системе сохраняется. Так как
,
то
,
.
Под действием упругой силы тело совершает гармонические колебания с циклической частотой:
,
так как ускорение тела пропорционально смещению
При наличии силы трения колебания будут затухающими.