15.4. Передача енергії стаціонарним полем
З рівнянні Максвела для стаціонарного поля випливає, що його магнітне поле соленоїдальне (магнітні силові лінії замкнуті), а електричне - потенційне (електричні силові лінії спираються на заряди). Електромагнітне поле такої структури, що передає енергію у визначеному напрямку, може бути отримане за допомогою двох дротів , що йдуть у цьому напрямку, заряди по яких рухаються в протилежних напрямках. Електричні силові лінії спираються на ці заряди (рис.17).
Рис.17. Передача електромагнітної енергії постійним струмом.
а - схема; б - структура поля в перетині аб.
Теорема
Умова-Пойтінга
для стаціонарного поля (де
)
має наступний
вигляд:
Ліва частина цього виразу стосовно до рис.17 може бути подана в наступному вигляді:
(1.53)
З цієї формули слідує, що передану стаціонарним полем потужність можна визначити як добуток різниці потенціалів між дротами на струм у дротах.
У цих
розрахунках ми не враховували втрати
енергії в дротах,
припускаючи, що їхня провідність
і тому на поверхні дротів
.
У дійсності ж (див. рис.18)
у поверхні провідника
вектор
має нормальну і тангенціальну складові,
унаслідок чого вектор Пойнтінга
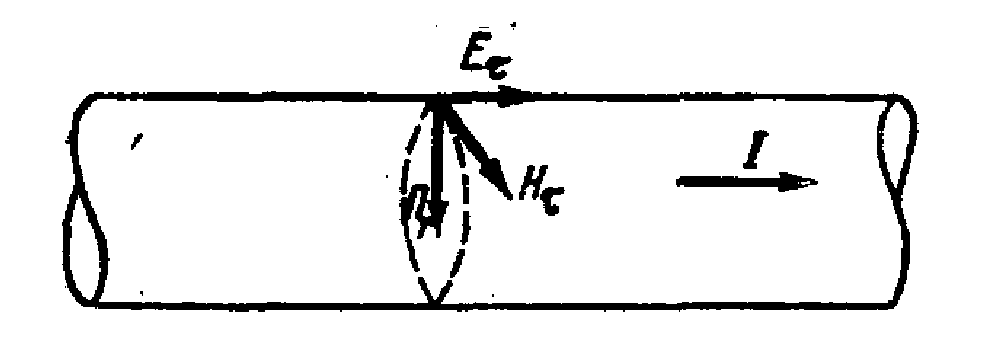
Рис.18. Складові поля в поверхні прямолінійного круглого дроту з струмом.
Перший
доданок у правій частині цієї формули
представляє
вектор, направлений
уздовж осі дротів,
і визначає енергію, яка
рухається
уздовж провідника
від джерела до навантаження. Другий
доданок - вектор, направлений
усередину провідника,
і
він
визначає енергію, яка
поглинається провідником.
Повна потужність,
що
поглинається кожним дротом
на
довжині
дорівнює:
(1.54)
де
- поверхня дроту
довжиною
.
У випадку
дротів
круглого перетину і достатньо великій
відстані між ними напруженість магнітного
поля поверхні дроту
.
Так
як
щільність
струму
,
то потужність,
яка
поглинається обома дротами
всієї
лінії
де
- опір обох дротів
лінії довжиною
.
Вираз (1.54) представляє закон Джоуля-Ленца. Отже, виділення тепла струмом є результат проникнення в провідник електромагнітного поля з зовнішнього простору.
Вектори
і
у будь-якій точці
лінії передачі направлені
так, що енергія поширюється уздовж
дротів
від джерела до навантаження; при цьому
передача енергії здійснюється в просторі,
оточуючим
дроти,
а не усередині дротів.
Проте щільність
енергії - найбільша
в безпосередній близькості до поверхні
дротів,
де напруженість електричного і магнітного
полів
найбільша.
У
навантаженні
вектор Пойнтінга
направлений
усередину, тобто електромагнітна енергія
входить у навантаження, перетворюючись
в інший
вид
енергії. У джерела енергії вектор
направлений
у зовнішнє середовище.
Внаслідок наявності опору дротів
на їх поверхні з'являється
тангенціальна складова
;
тому частина енергії проникає усередину
дротів,
перетворюючись у тепло.
Потужність, що віддається джерелом (з урахуванням втрат у дротах), відповідно до формули (1.53)
Напруга
вимірюється в джерелі
енергії. Потужність, яка
поглинається в дротах,
визначається формулою (1.54),
унаслідок цього корисна потужність у
навантаженні
а к.к.д. лінії передачі постійного струму
т. ч.
він зростає при збільшенні
між дротами.