15.3. Електричне поле постійного струму в провідному середовищі. Електричний опір.

Електричне стаціонарне поле всередині однорідного, ізотропного провідного середовища, що не містить сторонніх джерел струму, характеризується рівняннями:

(1.50)

Ці рівняння виражають у диференціальній формі відповідно закон Ома, перший і другий закони Кірхгофа.

Електричне поле , яке підтримує струм у провідній середі і переміщує об'ємний заряд, робить на ділянці роботу

яка перетворюється в тепло. На підставі цієї формули потужність втрат в одиниці об'єму провідної середи

(1.51)

тут - середня швидкість руху зарядів у провідній середі.

Ця формула виражає в диференціальній формі закон Джоуля-Ленца.

Якщо рівняння (1.50) порівняти з рівняннями, що описують електричне поле в діелектричній області, яка не містить вільних зарядів: , а також граничні умови для електростатичного поля з граничними умовами для стаціонарного поля, то можна зробити наступний висновок: рішення задач, пов'язаних з електричним стаціонарним полем в провідній середі, відповідають рішенням задач, пов'язаних з електростатичним полем в діелектричній середі, при заміні в останніх на і на .

Очевидно, вірно й зворотне, рішення задач, зв'язаних із стаціонарним полем, можна застосовувати до задач статичного поля при заміні на і на .

Рішення задач, зв'язаних із магнітним статичним полем, що описується рівняннями , також можна використовувати для визначення електричного стаціонарного поля при заміні на , на і на .

Відповідно до рівнянь (1.50) інтеграл, взятий по замкнутому контуру, що збігається з лінією струму (рис.16 а) для лінійної середи дорівнює

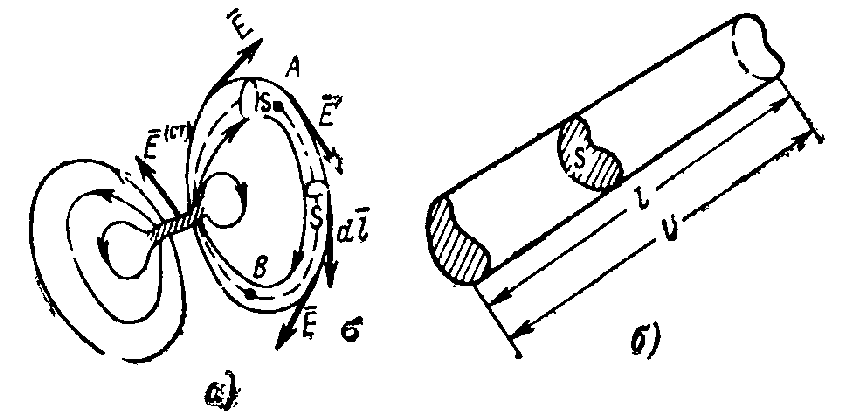
Рис.16. До визначення опору в середовищі (а) і опори провідника кінцевих розмірів (б)

Так як інтеграл по замкнутому контуру дорівнює нулю, із попереднього виразу слідує, що , інакше кажучи, існування струму при наявності тільки потенційного поля неможливо. У цьому випадку струми можуть існувати тільки при наявності ще і стороннього поля з напруженістю . При цьому інтеграл, узятий уздовж струмової трубки, можна представити у вигляді

з огляду на те, що , одержуємо:

де -електрорушійна сила (е.р.с.), яка обумовлена роботою по переміщенню одиничного заряду по замкнутому контуру.

З огляду на те, що вектори і по напрямку збігаються, ліву частину попереднього виразу можна представити в наступному вигляді:

де - поперечний перетин достатньо тонкої струмової трубки; - струм , що протікає через її електричний опір.

Отже,

Якщо інтегрування провадиться не по замкнутому контуру, а на обмеженій ділянці , де стороннє поле відсутнє, то

або

(1.52)

де - напруга на ділянці ; і - електричний опір і провідність ділянки .

Якщо провідна середа представляє провідник кінцевих розмірів (рис.16 б), до кінців якого прикладена різниця потенціалів і який оточений середою, що не проводить, то, рахуючи електричне поле однорідним по перетину , одержуємо вираз, аналогічний (1.52), де - електричний опір провідника.

Вираз (1.52) представляє закон Ома в інтегральній формі. Електричний опір провідника називають також омічним.

Потужність втрат у провіднику

У цьому виразі інтегрування провадиться відповідно по об’єму і довжині провідника. Останній вираз представляє закон Джоуля-Ленца в інтегральній формі для провідника.

Якщо підставити в нього (1.52), одержимо:

Якщо порівняти вирази

і

де

то можна зробити висновок, що при заміні на формула ємності переходить у формулу провідності і навпаки.

Цей метод застосовується для визначення електричного опору деяких провідних тіл із кінцевими розмірами.