4. Вторинні параметри однорідної лінії

Вторинними або характеристичними параметрами лінії є коефіцієнт затухання , коефіцієнт фази  і хвильовий опір , які в свою чергу виражаються через первинні параметри лінії та частоту.

З виразу

(1.19)

Спільне вирішення цих рівнянь дає:

(1.20)

(1.21)

Одержані вирази показують, що  та  в загальному випадку залежать від частоти. Проте, у відміну від коефіцієнту затухання, що змінюється в обмежених межах, коефіцієнт фази необмежено росте з частотою.

Формула (1.21) дозволяє виразити фазову швидкість хвилі через первинні параметри лінії та частоту.

Нижче буде показане, що для ліній без спотворень (r₀/g₀=L₀/C₀) і для ліній без втрат (r₀=0; g₀=0)

Де с₀ - швидкість світла у вакуумі _r і _r - відносні діелектрична та магнітна проникливості діелектрика, оточуючого провід.

У повітряних лініях _r  1 і _r  1 і за відсутності втрат швидкість хвиль практично рівна c₀. У кабелях _r4-5 швидкість хвиль у 2-2,5 раз менше с₀. У повітряних лініях із втратами фазова швидкість менше c₀.

На рис.6 показаний характер зміни  та  в залежності від частоти. Коефіцієнт  із зростанням частоти асимптотично наближається до прямої, яка утворює з віссю  кут , де m - масштабний коефіцієнт.

Рис 6. Частотні характеристики  та .

Хвильовий опір лінії

(1.22)

При постійному струмі ( = 0) і при частоті ( = ) має відповідно дійсні значення:

;

;

В інший частині діапазону частот хвильовий опір лінії має ємнісний характер, бо звичайно .

На рис.7 показані криві зміни модуля і кута  хвильового опору лінії в залежності від частоти.

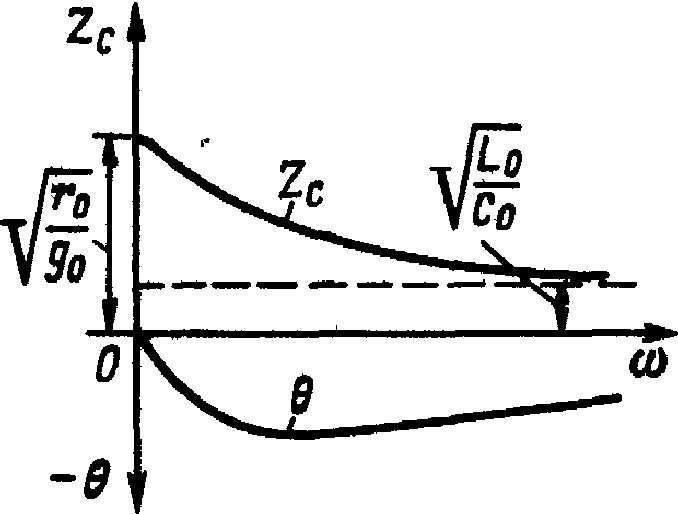
Рис.7 Залежність модуля та кута хвильового опору лінії від частоти.

Середні значення модуля для повітряних ліній 300-400 Ом, а для кабелів 60-80 Ом. У кабелів ємність С₀ значно більше, а індуктивність L₀ менше, ніж у повітряних ліній, бо дроти кабелю розміщені ближче друг до друга, а відносна діелектрична проникливість ізоляції - порядку 4 - 5. Тому кабелів у 6-8 разів менший, чим повітряних.

5. Вхідний опір лінії

При дослідженні процесів в лінії часто важливо знати вхідний опір лінії. Під вхідним опором лінії розуміють опір двополюсника, яким можна замінити лінію разом з навантаженням на її кінці при розрахунку режиму на початку лінії. Вхідний опір лінії, поміряний у довільній точці на відстані х' від кінця, визначається відношенням і може бути представлений в комплексній або гіперболічній формі. Будемо рахувати, що лінія навантажена на кінці деяким опором , який в залежності від умов може бути будь-яким.

Комплексна форма виразу для вхідного опору лінії одержується на підставі (1.13).

Або

(1.23)

Даний вираз показує, що з зміною координати х' модуль вхідного опору лінії коливається між деякими максимумами та мінімумами (які в загальному випадку відрізняються друг від друга).

Припустимо, що модуль досягає деякого максимума у точці x'_ext. Тоді максимуми будуть також у точках, відповідних зміні аргументу 2x на величину 2k, що дає:

2'_ext+2k = 2 (x'_ext+k/) =2 (x'_ext+k/2)

Отже, максимуми чергуються через кожні півхвилі Посередині між максимумами будуть мінімуми, що також чергуються через кожні півхвилі.

Хвилеподібний характер кривої підлягає у загальному випадку закону зміни модуля гіперболічного тангенса з комплексним аргументом, що видно з наступного висновку.

Безпосередньо з (1.17) слідує

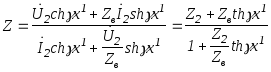(1.24)

При холостому ході (Z₂=) вхідний опір лінії згідно (1.24):

(1.25)

А при короткому замиканні (Z₂=0)

(1.26)

З урахуванням (1.25) та (1.26) вхідний опір Z легко виразити через Z_х та Z_к:

Цією формулою користуються у тому випадку, коли з дослідів холостого ходу та короткого замикання відомі Z_х та Z_к.

Дані дослідів холостого ходу та короткого замикання використовуються також для обчислення характеристичних параметрів лінії.

На підставі (1.25) та (1.26)

(1.27)

Зважаючи на те, що коефіцієнт фази  визначається по (1.27) неоднозначно, при обчисленні провадиться перевірка на підставі виразу для , причому первісно фазова швидкістьобирається орієнтовно.

На рис.8 показані криві зміни модулів Z_х та Z_к в залежності від координати х'. Аналіз показує, що Z_вх та  _вх змінюються хвилеподібно як при зміні довжини лінії l, так і при зміні частоти f.

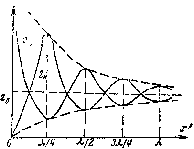
Рис. 8. Вхідні опору лінії при холостому ході та короткому замиканні.

В границі, т. ч. при x', максимуми та мінімуми кривої прагнуть до значення Z_в