2.6. Единицы количества информации

Существует два подхода к понятию количества информации: вероятностный, который ввел один из основоположников кибернетики американский математик Клод Шеннон, и объемный подход.

Количеством информации при вероятностном подходе называют числовую характеристику сигнала, отражающую ту степень неопределенности (неполноту знаний), которая исчезает после получения сообщения в виде данного сигнала. В качестве иллюстрации рассмотрим опыт, связанный с бросанием правильной игральной кости, имеющей n граней (часто n = 6). Результатом данного опыта может быть выпадение грани с одним из номеров: 1, 2, 3, …, n.

Введем в рассмотрение численную величину, измеряющую неопределенность – энтропию. Обозначим ее буквой H. Величины n и H связаны некоторой функциональной зависимостью:

, (2.1)

где функция f является возрастающей, неотрицательной и определенной для n = 1, 2, …, 6.

Рассмотрим процедуру бросания кости.

1. Готовимся бросить кость. Исход опыта неизвестен. Имеется некоторая неопределенность .

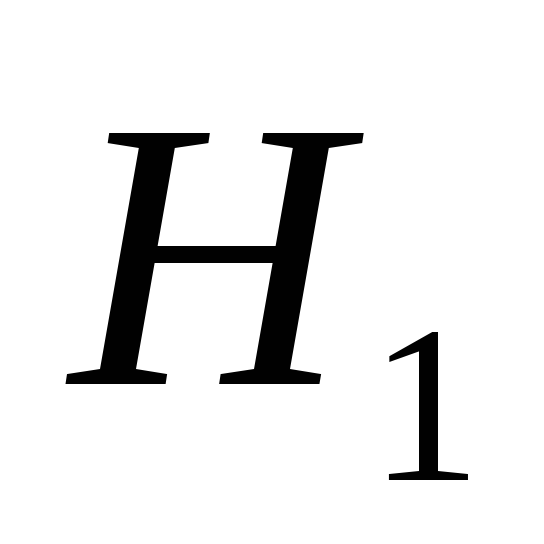2. Кость брошена. Информация об исходе опыта получена. Обозначим количество этой информации через I.

3. Обозначим неопределенность опыта после его осуществления через .

За количество информации, полученной в ходе осуществления опыта, принимают разность неопределенностей «до» и «после» опыта:

. (2.2)

Если в результате получения сообщения достигается полная ясность в каком-то вопросе, то говорят, что получена полная или исчерпывающая информация и необходимости в получении дополнительной информации нет. Наоборот, если после получения сообщения неопределенность осталась прежней, значит информации получено не было (нулевая информация). В нашем примере с игральной костью, когда получен конкретный результат, имевшаяся неопределенность снята, т.е. . Таким образом, количество полученной информации совпадает с первоначальной энтропией, и неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта. Но, как было сказано выше, могло и не быть равным нулю.

Важным вопросом является определение вида функции f в формуле (2.1). Предположим, что какое-то событие имеет n равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего n таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число N возможных комбинаций букв алфавита, то есть число возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = n, если из двух, то . Если сообщение содержит m символов (m – длина сообщения), то . Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности исхода опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т.е. когда n = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при n = 1 не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с и числом возможных сообщений общее число возможных сообщений , в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.

Для выхода из положения была предложена формула

H = log N. (2.3)

Формула (2.3) есть формула Хартли, определяющая связь между количеством информации и числом состояний системы. Эта формула удовлетворяет предъявленным выше требованиям. Поэтому ее можно использовать для измерения количества информации. Действительно, если все множество возможных сообщений состоит из одного (N = n = 1), то

H = log 1 = 0,

что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с и числом возможных сообщений

,

т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь.

Итак, Хартли предложил определять количество информации в физической системе, основываясь на числе ее возможных состояний. При этом он считал все состояния системы равновероятными, и в этом был главный недостаток формулы Хартли.

При введении какой-либо величины важно знать, что принимать за единицу ее измерения. Пусть основание логарифма равно 2. Тогда H = 1 при N = 2. В качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов. Такая единица количества информации называется бит (англ. bit – Binary digiT). Или, битом называется количество информации, которое можно получить при ответе на вопрос типа «да / нет». Бит – минимальная единица количества информации. Получить информацию, меньшую, чем один бит невозможно. При получении информации в 1 бит неопределенность уменьшается в два раза.

При объемном подходе, битами называются знаки 0 и 1 в двоичной системе счисления. В компьютере предпочтение отдается двоичной системе счисления. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера, подсчитывается по количеству требуемых для такой записи двоичных символов. При этом невозможно нецелое число битов (в отличие от вероятностного подхода).

Группа из 8 битов информации называется байтом. Если бит минимальная единица информации, то байт ее основная единица. Существуют производные единицы информации:

1 Кб = 1024 байта = (1024) байт

1 Мб = 1024 Кб = (10241024) байт

1 Гб = 1024 Мб = (102410241024) байт

Эти единицы чаще всего используются для указания объема памяти ЭВМ.