Раздел 2. Интегральное исчисление

2.1. Первообразная функция и неопределенный интеграл

Пусть функция f(x) определена на некотором (конечном или бесконечном) интервале (а; b). Функция F(x) называется первообразной для функции f(x) на интервале (а; b), если в любой точке этого промежутка ее производная равна f(x), т. е.

для всех или dF(x)= f(x)dx.

Если F(x) есть одна из первообразных для функции f(x), то всякая другая представляется выражением F(x)+C, где C – произвольная постоянная величина. Таким образом, любая непрерывная функция f(x) имеет бесчисленное множество первообразных.

Неопределенным интегралом от функции f(x) (или от выражения f(x)dx) называется совокупность всех ее первообразных.

Обозначение: .

Здесь знак называется интегралом, функция f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением, х – переменной интегрирования.

2.2. Основные свойства неопределенного интеграла

1. Неопределенный интеграл от дифференциала функции равен этой функции плюс произвольная постоянная:

.

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:

3. Неопределенный интеграл суммы функций равен сумме неопределенных интегралов этих функций:

.

4. Постоянный множитель 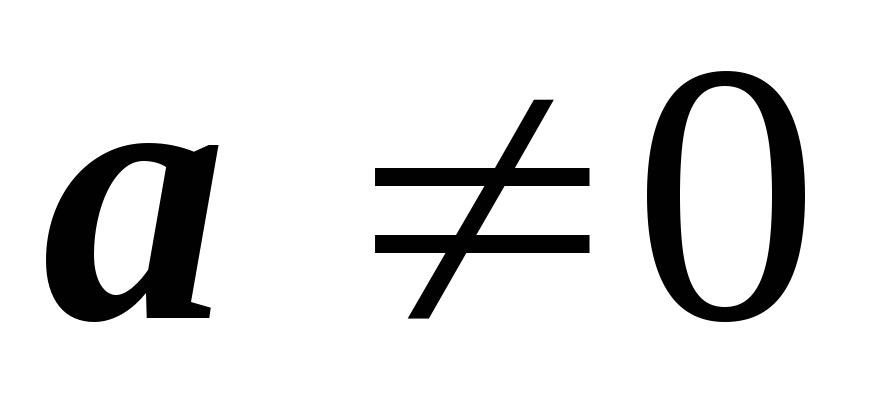можно выносить за знак неопределенного интеграла:

.

5. Если F(x) первообразная для функции f(x), то 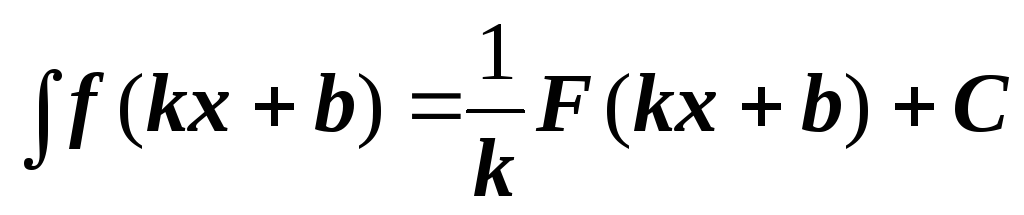, где k и b – постоянные.

2.3. Таблица простейших интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. ,

14. 

15. ,

16. 

17. 

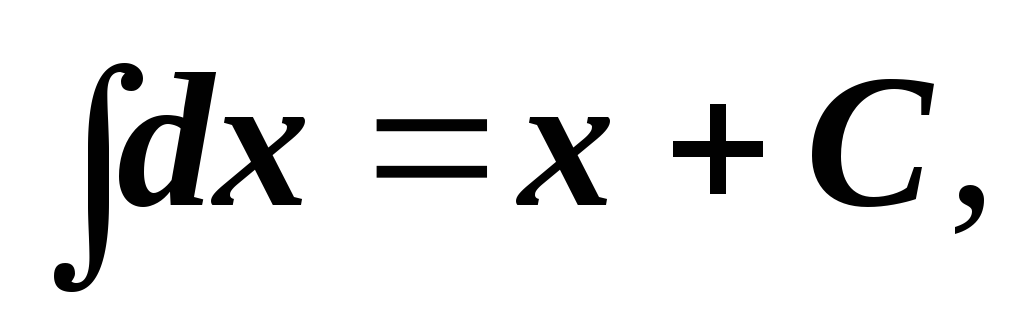
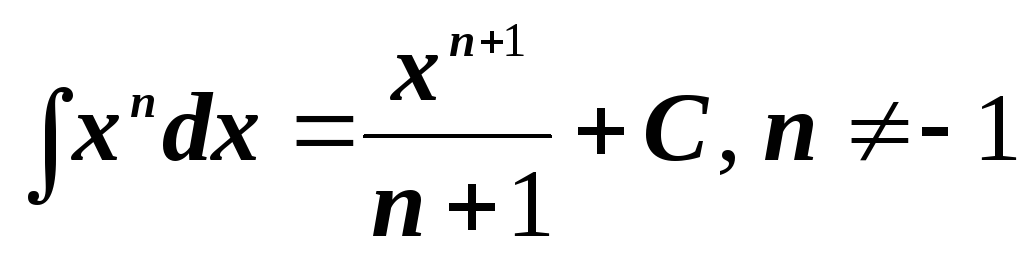
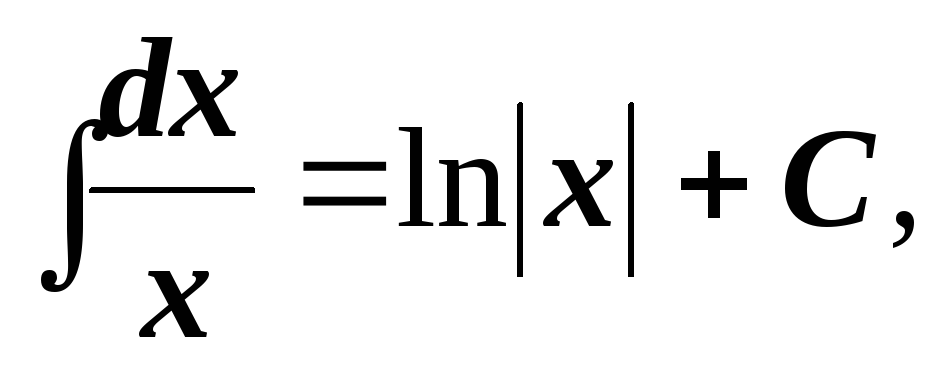
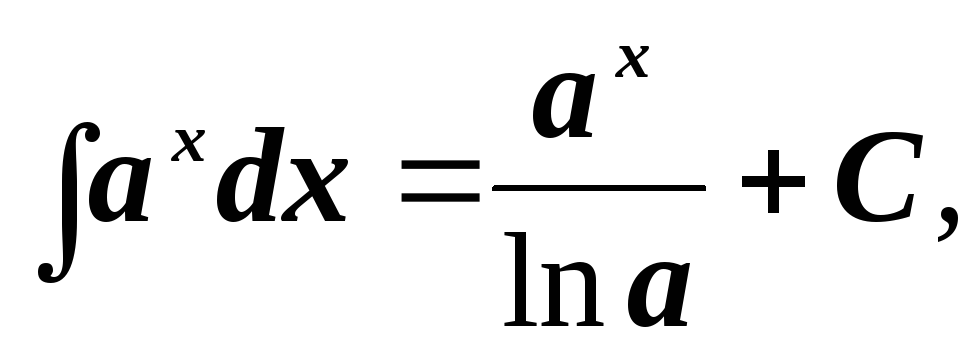
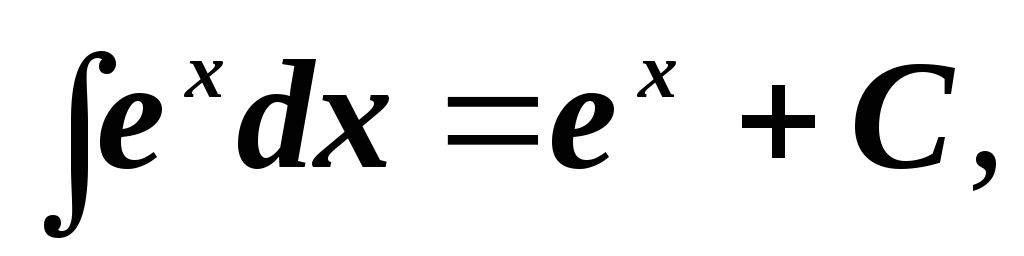
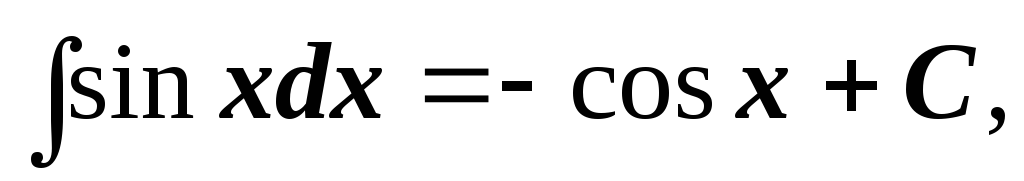
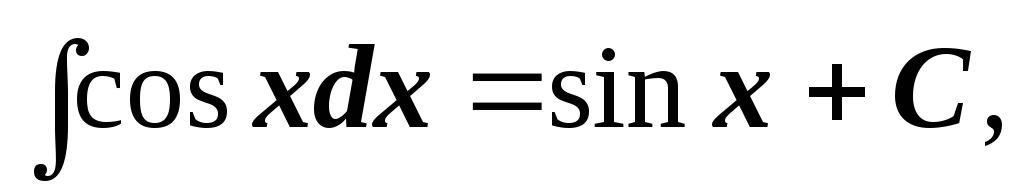
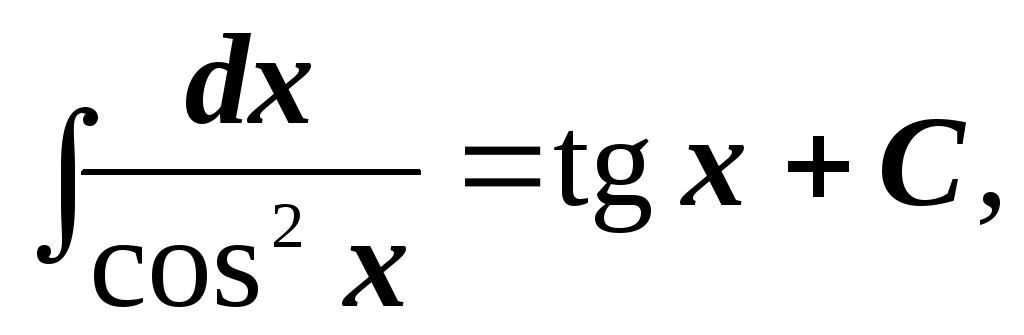
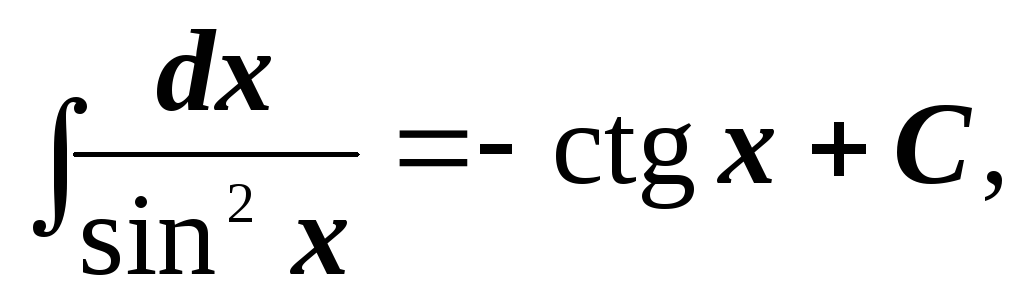
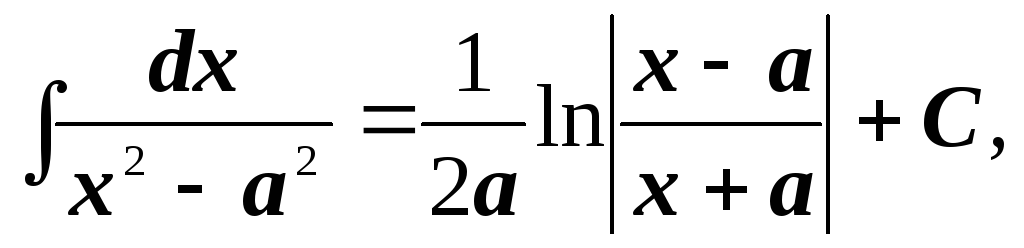
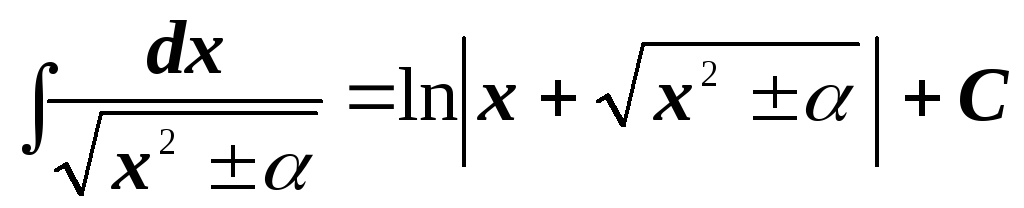
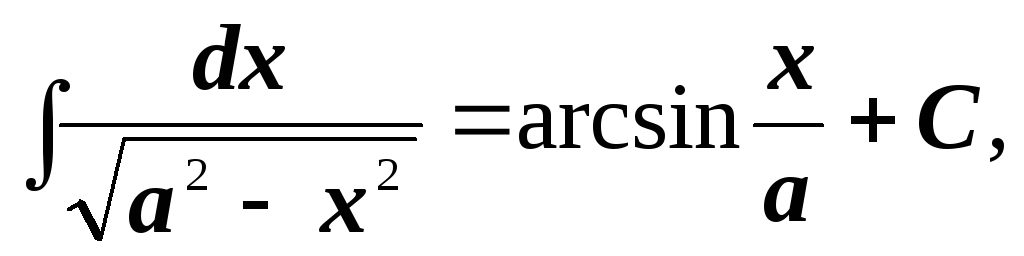
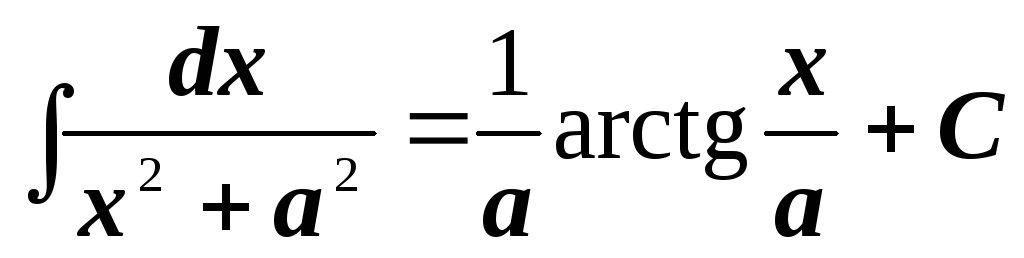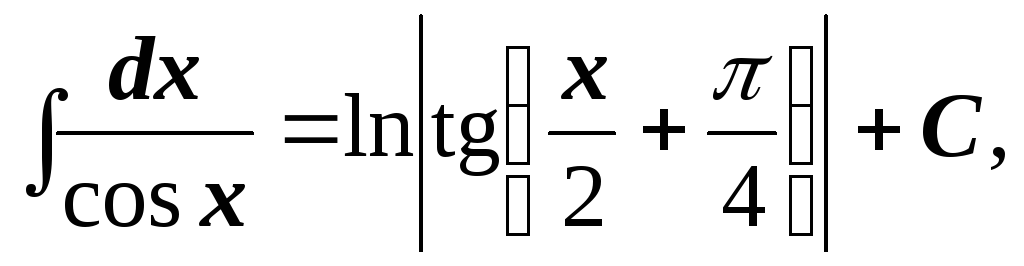
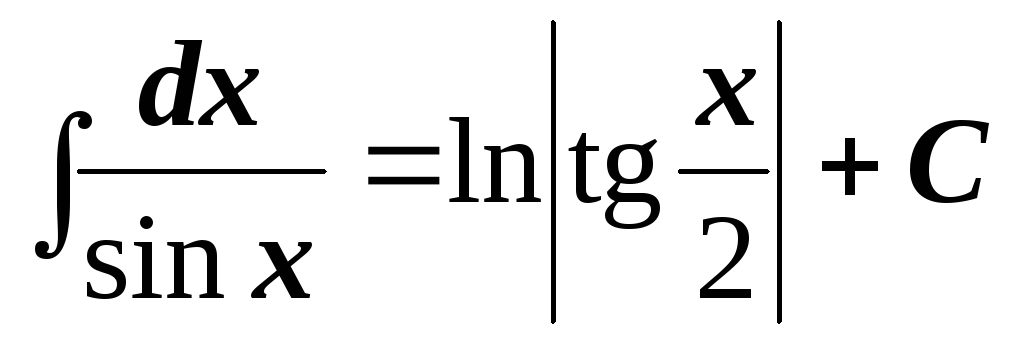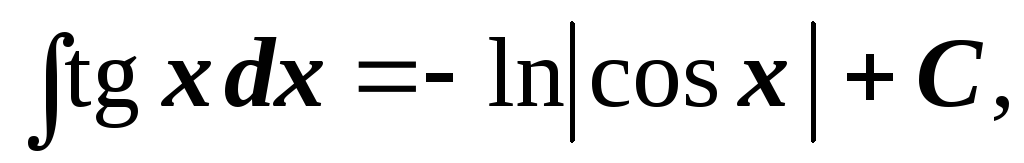
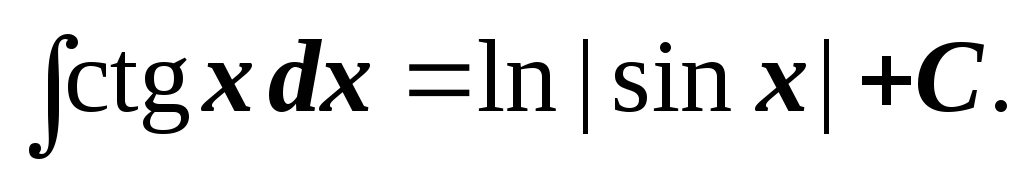
2.4. Основные методы интегрирования

1) Непосредственное интегрирование. Способ непосредственного интегрирования основан на использовании свойств неопределенного интеграла и приведении подынтегрального выражения к табличной форме.

2) Метод подстановки (замена переменной). Этот способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:

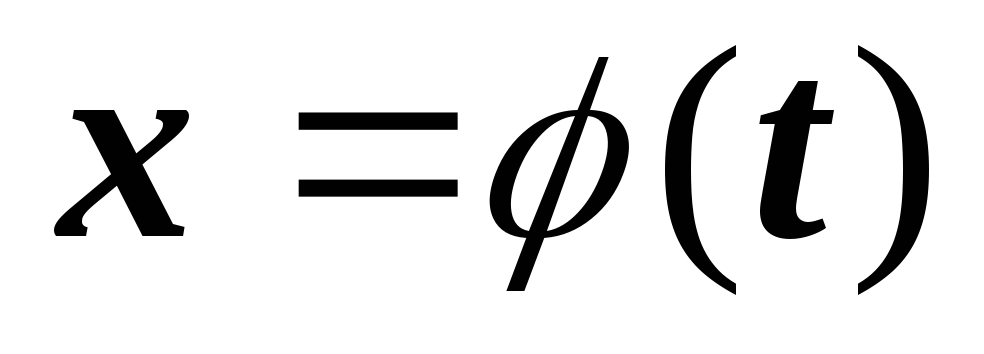1. , где t – новая переменная, а φ(t) – функция, имеющая непрерывную производную. Тогда формула замены переменной

.

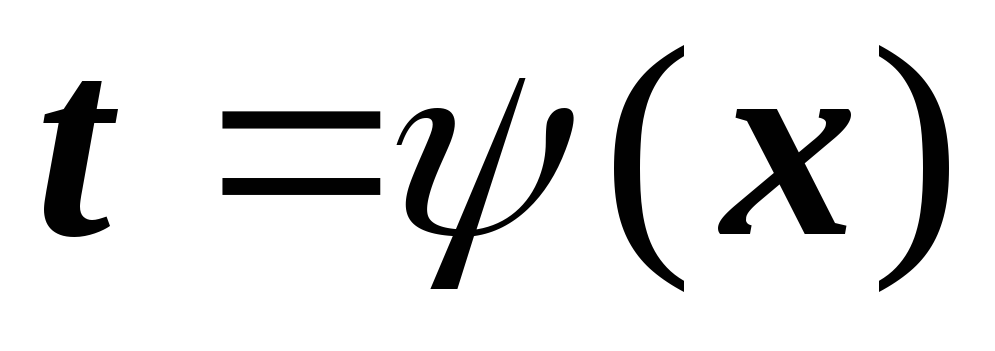2. , t – новая переменная. Формула замены переменной при такой подстановке:

3) Интегрирование по частям. Интегрированием по частям называется нахождение интеграла по формуле

, (2.4.1)

где u и v непрерывно дифференцируемые функции от х. С помощью формулы (2.4.1) нахождение интеграла сводится к нахождению другого интеграла . Применение этой формулы целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.

При этом в качестве u берется функция, которая при дифференцировании упрощается, а в качестве dv – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.