1 Расчет тарельчатой ректификационной колонны непрерывного действия.

1. Материальный баланс колонны и рабочее флегмовое число.

Производительность колонны по дистилляту Р и кубовому остатку W определим из уравне­ний материального баланса колонны:

(1.1)

где F, P и W – производительность колонны по исходному веществу, по дистилляту и по ку-бовому остатку, соответственно, кг/с.

(1.2)

Отсюда находим:

(1.3)

где , и - массовые доли по дистилляту, исходной смеси и кубового остатка, соответственно, кг/кг смеси.

Пересчитаем составы фаз из мольных долей в массовые доли по соотношению:

(1.4)

где , и - мольные доли по дистилляту, исходной смеси и кубового остатка соответственно, кмоль/кмоль смеси;

, - молекулярные массы соответственно этилацетата и толуола, кг/кмоль.

(1.5)

(1.6)

Находим производительность по кубовому остатку:

Находим производительность колоны по дистилляту:

Нагрузки ректификационной колоны по пару и жидкости определяется рабочим флегмовым числом R; его оптимальное значение R_опт можно найти путём технико-экономического рас­чёта. Ввиду отсутствия надёжной методики оценки R_опт используют приближённые вычис­ления, основанные на определении коэффициента избытка флегмы (орошения) Здесь - минимальное флегмовое число:

(1.7)

где и - мольные доли легколетучего компонента соответственно в исходной смеси и дистилляте, кмоль/кмоль смеси;

- концентрация легколетучего компонента в паре, находящемся в равновесии с ис-ходной смесью, кмоль/кмоль смеси.

Один из возможных приближённых методов расчёта R заключается в нахождении такого флегмового числа, которому соответствует минимальное произведение N(R+1), пропор-циональное объёму ректификационной колонны (N – число ступеней изменения концент-рации или теоретических тарелок, определяющее высоту колонны, а (R+1) − расход паров и, следовательно, сечение колонны).

Задавшись различными значениями коэффициентов избытка флегмы , определим соот-ветствующие флегмовые числа.

(1.8)

Графическим построением ступеней изменения концентраций между равновесной и рабочими линиями на диаграмме состав пара Y – состав жидкости X, находим число ступеней N. Равновесные данные приведены в справочнике [3 с.36].

Результаты расчётов рабочего флегмового числа, представлены на рисунке 2 и приведены ниже:

Рисунок 2 — Изображение рабочих линий в диаграмме y – x при действительном флегмовом числе

Таблица 1 – Результаты расчетов рабочего флегмового числа

	1,050	1,350	1,750	2,350	3,300
R	1,813	2,129	2,760	3,706	5,204
N	19	15	12,5	11	10
N(R+1)	53,447	46,935	47,000	51,766	62,040

Рисунок 3 – Определение рабочего флегмового числа.

Минимальное произведение N(R+1) соответствует флегмовому числу R=2,023. При этом коэффициент избытка флегмы На рисунке 2, изображены рабочие линии и ступени изменения концентраций для верхней (укрепляющей) и нижней (исчерпывающей) частей колоны в соответствии с найденным значением R.

Средние массовые расходы (нагрузки) по жидкости для верхней и нижней частей колонны определяют из соотношений:

(1.9)

(1.10)

где и - мольные массы дистиллята и исходной смеси;

и - средние мольные массы жидкости в верхней и нижней частях колонны.

Мольную массу дистиллята в данном случае можно принять равной мольной массе легколетучего компонента – этилацетат. Средние мольные массы жидкости в верхней и нижней частях колонны соответственно равны:

(1.11)

(1.12)

где и - мольные массы этилацетата и толуола;

и - средний мольный состав жидкости соответственно в верхней и нижней частях колонны:

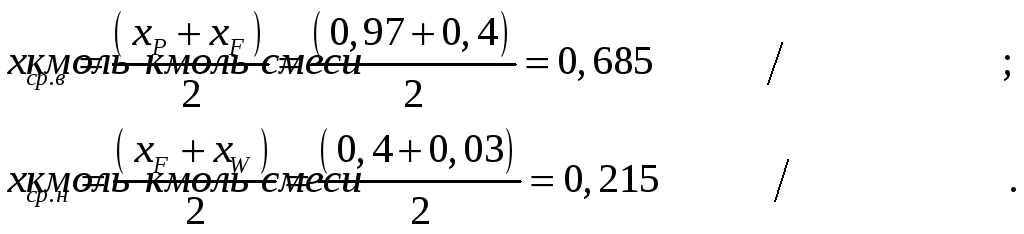
Тогда

Мольная масса исходной смеси:

Подставим рассчитанные величины в уравнения (1.9) и (1.10), получим:

Средние массовые потоки пара в верхней и нижней частях колоны соответственно равны:

(1.13)

(1.14)

где и - средние мольные массы паров в верхней и нижней частях колонны:

(1.15)

(1.16)

где и - мольные массы этилацетата и толуола, [3 c.36];

и - средний мольный состав пара соответственно в верхней и нижней частях колонны:

Тогда

Подставим численные значения в уравнение , получим:

1.2 Определение плотности и вязкости

Найдём плотности жидкости , и пара , в верхних и нижних час-тях колонны, при средних температурах в них .

Средние температуры паров определим по диаграмме по средним составам фаз: [3 c.36].

Тогда

(1.17)

(1.18)

Отсюда получим:

Плотность физических смесей жидкостей подчиняется закону аддитивности:

(1.19)

где - объёмная доля компонента в смеси;

, - плотности компонентов, при средней температуре жидкости вверху и внизу колонны, кг/м³.

Произведём пересчёт из мольных долей в объёмные доли для этилацетата вверху колонны:

(1.20)

где - мольная доля этилацетата в дистилляте;

,,, - плотности и мольные массы этилацетата и толуола при 20 ⁰С соответственно,[3 c.36].

Произведём пересчёт из мольных долей в объёмные доли для этилацетата в кубовой части колонны:

где - мольная доля этилацетата в кубовой части колонны;

,,, - плотности и мольные массы этилацетата и толуола при 20 ⁰С соответственно, [3 c.36].

Подставим в уравнение (1.20), получим:

Вязкость жидких смесей находим по уравнению:

(1.21)

где и - вязкости жидких этилацетата и толуола при температуре смеси, Па∙с

[2 рис. V c. 556].

(1.22)

Подставив численные значения, получим:

Необходимо определить вязкость паров и коэффициенты диффузии в жидкой и паровой фазах. Вязкость паров для верхней части колонны:

(1.23)

где и - вязкость паров этилацетата и толуола при средней температуре верхней части колонны, [3 c.36], мПас;

Примечание: так как нет надёжных данных для определения вязкости паров этилацетата, поэтому берём вязкость паров для диэтилового эфира.

- средняя концентрация паров:

Подставив, получим:

Аналогично расчётом для нижней части колонны находим

(1.24)

Коэффициент диффузии в жидкости при средней температуре t (в ⁰С) равен:

(1.25)

Коэффициенты диффузии в жидкости при 20 ⁰С можно вычислить по приближенной формуле:

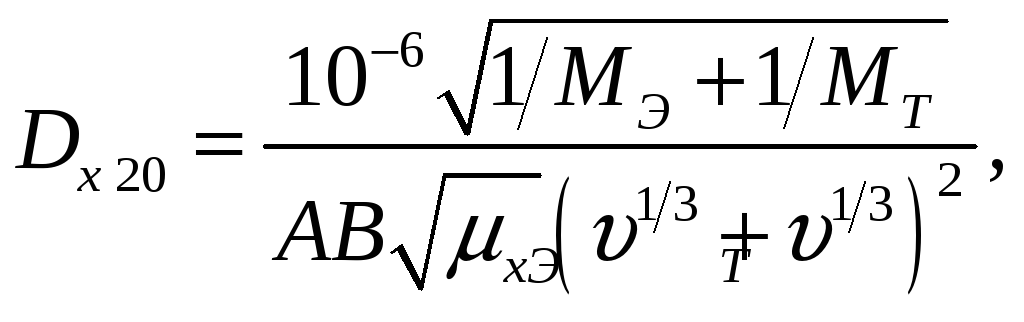(1.26)

где А, В – коэффициенты, зависящие от свойств растворённого вещества и растворителя;

- мольные объёмы компонентов в жидком состоянии при температуре кипения, см³/моль;

- вязкость жидкости при 20 ⁰С, мПа∙с,[2 табл. V c.556].

Вычислим вязкость жидкости для верхней части колонны при температуре 20 ⁰С:

Вычислим вязкость жидкости для нижней части колонны при температуре 20 ⁰С:

Тогда коэффициент диффузии в жидкости для верхней части колонны при 20 ⁰С равен:

Температурный коэффициент b определяют по формуле:

(1.27)

где и принимают при температуре 20 ⁰С, [2 табл. V c.556 и 3 с.36].

Плотность жидкости при 20 ⁰С в верхней и нижней частей колонны найдём по формуле:

Тогда

Тогда

Подставим полученные численные значения для определения температурного коэффициен-та:

Отсюда

Аналогично для нижней части колонны находим:

Коэффициент диффузии в жидкости для нижней части колонны при 20 ⁰С равен:

Температурный коэффициент b определяют по формуле:

Тогда коэффициент диффузии в жидкости для нижней части колонны:

1.3 Скорость пара и диаметр колонны

Допустимая скорость в верхней и нижней частях колонны соответственно равна:

(2.29)

(2.30)

Ориентировочный диаметр колонны определяют из уравнения расхода:

(2.31)

Как правило, несмотря на разницу в рассчитанных диаметрах укрепляющих и исчерпывающей частей колонны (вследствие различия скоростей и расходов паров), изготовляют колонну единого диаметра, равного большему из рассчитанных.

В данном случае скорости и мало отличаются друг от друга; используем в расчете среднюю скорость паров:

Принимаем средний массовый поток пара в колонне равным полусумме :

Средняя плотность паров:

Диаметр колонны

Выберем стандартный диаметр обечайки колонны [1 разд. 5.1.4 c.197].

При этом рабочая скорость пара:

По каталогу для колонны диаметром 1600 мм выбираем ситчатую однопоточную тарелку ТСР со следующими конструктивными размерами [1 c.216]:

Диаметр отверстий в тарелке

Шаг между отверстиями t=16 мм

Относительное свободное сечение тарелки

Высота переливного порога

Ширина переливного порога

Рабочее сечение тарелки

Скорость пара в рабочем сечении тарелки

(2.32)

где - рабочее сечение тарелки, м²;

- диаметр колонны, м;

- рабочая скорость пара, м/с.

1.4 Высота колонны.

Число действительных тарелок в колонне может быть определено графоаналитическим методом (построением кинетической линии). Для этого необходимо рассчитать общую эффективность массопередачи на тарелке (к. п. д. по Мэрфри). Эффективность тарелки по Мэрфри с учетом продольного перемешива­ния, межтарельчатого уноса и доли байпаси-рующей жидкости приближенно опреде­ляется следующими уравнениями:

(2.33)

(2.34)

(2.35)

(2.36)

где − фактор массопередачи для укрепляющей части колонны;

− фактор массопередачи для исчерпывающей части колонны;

− локальная эффективность по пару;

е − межтарельчатый унос жидкости, кг жидкости/кг пара;

− доля байпасирующей жидкости;

S— число ячеек полного перемешивания;

т — коэффициент распределения компонента по фазам в условиях равновесия.

Локальная эффективность Е_у связана с общим числом единиц переноса по паровой фазе на тарелке п_оу следующим соотношением:

(2.37)

где

(2.38)

где K_yf — в кмоль/(м²∙с);

М' — средняя мольная масса паров, кг/кмоль.

В настоящее время нет достаточно надежных данных для определения поверхности контакта фаз, особенно эффективной поверхности массопередачи при барботаже на тарелках. Поэтому обычно в расчетах тарельчатых колонн используют коэффициенты массопередачи, отнесенные к единице рабочей площади тарелки (K_yf). Коэффициент определяют по урав-нению аддитивности фазовых диффузионных сопротивлений:

(2.39)

где и — коэффициенты массоотдачи, отнесенные к единице рабочей площади тарелки соответственно для жидкой и паровой фаз, кмоль/(м²-с).

В частности, для определения коэффициентов массо­отдачи процессов ректификации бинарных систем, для тарелок барботажного типа рекомендуются обобщенные критериаль-ные уравнения типа, которые приводятся к удобному для расчетов виду:

(2.40)

(2.41)

1.5 Высота светлого слоя жидкости на тарелке и паросодержание барботажного слоя

Высоту светлого слоя жидкости для ситчатых тарелок находят по уравнению:

(2.42)

где − удельный расход жидкости на 1 м ширины сливной перегородки, м²/с;

− ширина сливной перегородки, м;

− высота переливной перегородки, м;

- в мПа∙с, [2 рис. V c.556];

m=0,05−4,6∙=0,05-4,6∙0,03=−0,088.

, - поверхностное натяжение соответственно жидкости и воды при средней тем-пературе в колонне, Н/м, [2 c.527].

.

где и - поверхностные натяжения соответственно для этилацетата и толуола, [2 c.527];

- массовая доля легколетучего компонента в исходной смеси.

Для верхней части колонны

Для нижней части колонны

Паросодержание барботажного слоя находят по формуле:

(2.43)

где

Для верхней части колонны:

Для нижней части колонны:

1.6 Коэффициенты массопередачи и высота колонны

Для верхней части колонны:

коэффициент массоотдачи в жидкой фазе

коэффициент массоотдачи в паровой фазе

Для нижней части колонны:

коэффициент массоотдачи в жидкой фазе

коэффициент массоотдачи в паровой фазе

Пересчитаем коэффициенты массоотдачи на кмоль/(м²∙с):

для верхней части колонны

для нижней части колонны

Коэффициенты массоотдачи, рассчитанные по средним значениям скоростей и физических свойств паровой и жидкой фаз, постоянны для верхней и нижней частей колонны. В то же время коэффициент массопередачи — величина переменная, зави­сящая от кривизны линии равновесия, т. е. от коэффициента распределения. Поэтому для определения данных, по которым строится кинетическая линия, необходимо вычислить несколько значений коэффициента массопередачи в интервале изменения состава жидкости от x_w до х_Р.

Пусть х = 0,03. Коэффициент распределения компонента по фазам (тангенс угла наклона равновесной линии в этой точке) т =2,933.

Коэффициент массопередачи K_yf вычисляем по коэффициентам массоотдачи в нижней части колонны:

.

Общее число единиц переноса на тарелку , находим по уравнению (2.38):

Локальная эффективность по уравнению (2.37) равна:

Для определения эффективности по Мэрфри необходимо рассчитать также фактор массопередачи , долю баипасирующеи жидкости , число ячеек полного пере­мешивания S и межтарельчатый унос е.

Фактор массопередачи для нижней части колонны:

.

Для ситчатых тарелок при факторе скорости долю баипасирующеи жидкости принимают

Для колонн диаметром более 600 мм с ситчатыми, колпачковыми и клапанными тарел-ками отсутствуют надежные данные по продольному перемешиванию жидкости, поэтому с достаточной степенью приближения можно считать, что одна ячейка пере­мешивания соответствует длине пути жидкости l=300—400 мм.

Примем l = 350 мм и определим число ячеек полного перемешивания S как отношение длины пути жидкости на тарелке l_т к длине l. Определим длину пути жидкости l_т, как расстояние между переливными устройствами:

(2.44)

Тогда число ячеек полного перемешивания на тарелке

Относительный унос жидкости е в тарельчатых колоннах определяется в основном скоростью пара, высотой сепарационного пространства и физическими свойствами жидкости и пара. В настоящее время нет надежных зависимостей, учитывающих влия­ние физических свойств потоков на унос, особенно для процессов ректификации. Для этих процессов унос можно оценить с помощью графических данных, представленных на рис. 6.7 [5]. По этим данным унос на тарелках различных конструкций является функцией комплекса . Коэффициент m учитывающий влияние на унос физи­ческих свойств жидкости и пара, определяют по уравнению:

(2.45)

Откуда

Высота сепарационного пространства Н_с равна расстоянию между верхним уровнем барботажного слоя и плоскостью тарелки, расположенной выше:

(2.46)

где Н — межтарельчатое расстояние, м;

h_П = h₀/(1 — ) —высота барботажного слоя (пены), м.

В соответствии с каталогом (10) для колонны с диаметром 1600 мм расстояние Н = 0,5 м.

Hc = 0,5 - 0,065 = 0,397 м

Тогда

При таком значении комплекса унос е = 0,12 кг/кг. Унос жидкости в верхней части колонны не отличается от уноса в верхней части е = 0,12 кг/кг

Подставляя в уравнения (2.33) — (2.36) вычисленные значения m, E_y, , S и e, опре­деляем к. п. д. по Мэрфи:

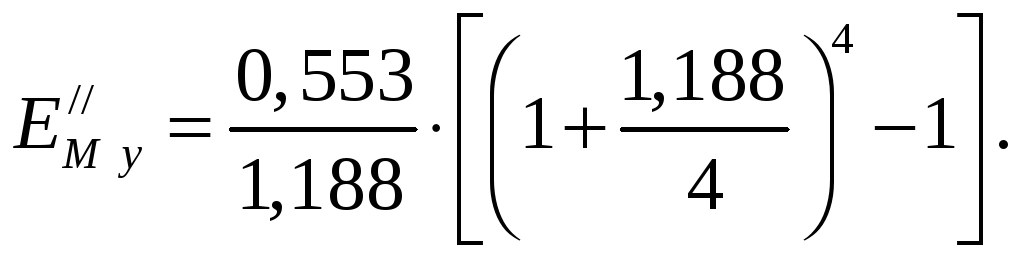
Зная эффективность по Мэрфри, можно определить концентрацию легколетучего компонента в паре на выходе из тарелке у_к по соотношению:

где у_н и у* — концентрация соответственно легколетучего компонента в паре на входе в тарелку и равновесная с жидкостью на тарелке.

Отсюда

Аналогичным образом подсчитаны у_к для других составов жидкости. Результаты расчета параметров, необходимых для построения кинетической линии, приведены ниже:

Таблица 2 - Результаты расчета параметров, необходимых для построения кинетической линии.

Параметр	Нижняя часть колонны				Верхняя часть колонны
X	0,03	0,2	0,3	0,4	0,6	0,8	0,9
M	2,933	2,14	1,843	1,65	1,335	1,14	1,063
Kyf	0,021	0,023	0,024	0,025	0,023	0,024	0,024
Noy	0,805	0,909	0,955	0,988	0,892	0,926	0,94
Ey	0,553	0,597	0,615	0,628	0,59	0,604	0,61
B	1,188	0,594	0,855	0,788	0,765	0,798	0,813
E11MY	0,852	0,847	0,843	0,839	0,832	0,842	0,846
E1MY	0,72	0,747	0,756	0,761	0,756	0,764	0,768
EMY	0,677	0,701	0,709	0,713	0,698	0,696	0,694
yk	0,069	0,386	0,519	0,64	0,777	0,895	0,946

Взяв отсюда значения х и y_к, наносят на диаграмму х — у точки, по которым проводят кинетическую линию (рис.4). Построением ступеней между рабочей и кинетической линиями в интервалах концентраций от х_Р до x_F определяют число действительных тарелок для верхней (укрепляющей) части N_B и в интервалах от x_F до x_w,— число действительных тарелок для нижней (исчерпывающей) части колонны N_H. Общее число действительных тарелок:

N=N_В+N_Н. (2.66)

N=19+12=31

Высоту тарельчатой ректификационной колонны определим по формуле

(2.67)

где h — расстояние между тарелками, м;

z_в ,z_н − расстояние соответственно между верхней тарелкой и крышкой колонны и между днищем колонны и нижней тарелкой, м.

Подставив, получим:

H_к=17,425м

Рисунок 4 – Определение числа действительных тарелок

1.7 Гидравлическое сопротивление тарелок колонны.

Гидравлическое сопротивление тарелок колонны Р_к определяют по формуле

(2.68)

где и — гидравлическое сопротивление тарелки соответственно верхней и нижней частей колонны, Па.

Полное гидравлическое сопротивление тарелки складывается из трех слагаемых

(2.69)

Гидравлическое сопротивление сухой ситчатой тарелки по уравнению (5.57) равно

(2.70)

где - коэффициент сопротивления сухих тарелок,

- скорость пара в рабочем сечении тарелки,

- средняя плотность паров, кг/м³;

- свободное сечение тарелки,

Гидравлическое сопротивление газожидкостного слоя на тарелках различно для верхней и нижней частей колонны:

(2.71)

(2.72)

где и - плотность жидкости соответственно вверху и внизу колонны, кг/м³,

и - высота светлого слоя жидкости, м.

Гидравлическое сопротивление, обусловленное силами поверхностного натяжения, равно:

(2.73)

(2.74)

где и - поверхностное натяжение жидкости при температуре соответственно вверху и внизу колонны, Н/м;

- эквивалентный диаметр отверстий в тарелке, м.

Тогда полное сопротивление одной тарелки верхней и нижней частей колонны равно:

Полное гидравлическое сопротивление ректификационной колонны:

2 Тепловой баланс ректификационной установки.

Тепловой баланс колонны имеет вид:

(2.1)

где - тепловая нагрузка, соответственно по исходному веществу, по кипятильнику, по дистилляту, по кубовому остатку, по дефлегматору и потери тепла, примем равными 5%.

Из баланса определяем количество тепла, которое необходимо подводить к кипятильнику.

Тепловая нагрузка по кубовому остатку, в количестве , рассчитывается по формуле:

(2.2)

где - теплоёмкость кубового остатка, при температуре , [2 рис. XI с. 562], ;

- температура кубового остатка колонны.

(2.3)

где - массовая доля кубового остатка.

Тепловая нагрузка по исходному веществу, в количестве кг/с, рассчитывается по формуле:

(2.4)

где - температуры смеси;

- теплоёмкость исходной смеси, при средней температуре, [2 рис. XI с. 562], .

(2.5)

где - массовая доля исходной смеси.

Подставим численные значения, получим:

Тепловая нагрузка аппарата по дистилляту, в количестве Р=1,153 кг/с, рассчитывается по формуле:

(2.6)

где - температура дистиллята, взятая из диаграммы t-х,y, ⁰С;

- теплоёмкость дистиллята, при температуре , [2 рис. XI с. 562], .

(2.7)

где - массовая доля дистиллята.

Подставим численные значения, получим:

Для дефлегматора тепловая нагрузка аппарата составит:

(2.8)

где - удельная теплота парообразования дистиллята, при , Дж/кг.

(2.9)

Подставим эти численные значения в уравнение теплового баланса и определим количество тепла, которое необходимо подводить к кипятильнику:

Для подогрева используют насыщенный водяной пар давлением 0,3 МПа. Темпе- ратура конденсации Характеристики конденсации при этой температуре: Расход греющего пара вычисляется по формуле:

(2.10)