6. Облигации с фиксированным купоном

Примерами облигаций с фиксированным купоном и погашением номинала в России являются облигации внутреннего валютного займа (ОВВЗ), выпускаемые с 1993 года, облигации Федерального займа с постоянным доходом (ОФЗ - ПД).

Доход по данным облигациям складывается из периодических купонных выплат и выплаты номинальной стоимости в конце срока. Доходы по купонам выплачиваются, как правило, один или два раза в году.

Таким образом, современная стоимость облигации с фиксированным купоном складывается из современной стоимости аннуитета и современной стоимости номинала. Если выплаты купонов происходят ежегодно, то рыночная цена облигации равна

, (²⁶)

где С - годовой купонный доход (в рублях), N - номинал облигации (в рублях), n - срок облигации (в годах), i - доходность к погашению или ставка дисконтирования.

Соотношения (Error: Reference source not found), связывают стоимость облигации или курс с доходностью к погашению. Если известна доходность i, то стоимость (или курс) можно определить с помощью соотношения (Error: Reference source not found). Обратная задача - определение доходности по курсу - в общем виде аналитически неразрешима. Поэтому доходность к погашению облигаций с фиксированным купоном находят с помощью численного решения уравнения (Error: Reference source not found).

Укажем на следующие особенности облигаций с постоянным купоном. Если облигация приобретена по номиналу (по курсу 100), то доходность к погашению i равна ставке купонного дохода g. Если облигация приобретена с дисконтом (по курсу меньше 100), то доходность больше купонного дохода (i > g). Если же облигация приобретена с премией (K > 100), доходность меньше купонного дохода (i < g). В последнем случае (при покупке с премией), владелец облигации также может получить доход, если не произойдет досрочного выкупа облигации эмитентом.

Если купонные выплаты происходят несколько раз в году, то часто для финансовых расчетов используется номинальная процентная ставка доходности j при условии начисления процентов m раз в году (m - количество выплат купонного дохода в году). Стоимость облигации с фиксированным доходом связана с номинальной ставкой доходности соотношением:

. (²⁷)

Заметим, что если годовой купонный доход равен С, а выплаты происходят m раз в году, то каждый раз выплачивается сумма, равная .

Часто при расчетах используют простую процентную ставку доходности для облигаций с фиксированным купоном. Напомним, что при начислении дохода по простой процентной ставке, доход каждый раз начисляется на первоначальную сумму, то есть предполагается, что доходы по процентам не реинвестируются. Поэтому можно записать:

, (²⁸)

откуда можно получить

, (²⁹)

Отметим, что простая доходность в некоторых случаях может сильно отличаться от сложной процентной ставки i.

Полная доходность i совпадает с простой , если облигация куплена по номиналу (K=100). В этом случае .

Также , если срок облигации равен одному году (n=1). Если срок облигации равен нескольким годам, то пользуются также другой приближенной формулой:

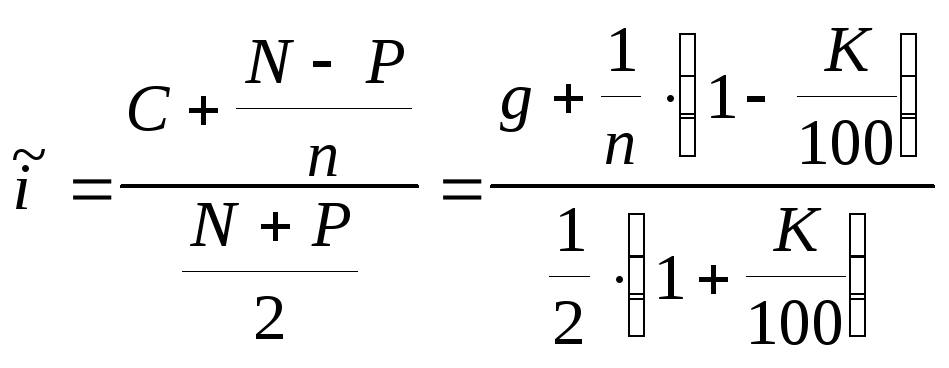. (³⁰)

Соотношение (Error: Reference source not found) отличается от (Error: Reference source not found) тем, что в (Error: Reference source not found) в знаменателе фигурирует не цена облигации, а средняя арифметическая между начальной ценой облигации P и конечной ценой N.

Пример 13. Срок облигации с фиксированным купоном равен 7 годам. Купонный доход выплачивается ежегодно по норме 12% от номинала в год. Найти курс облигации, если ставка дисконтирования принята равной 16%.

Решение:

Пример 14. Годовой купонный доход облигации равен 240 руб., купонный доход выплачивается 2 раза в году, номинал облигации равен 1300 руб., срок до погашения 6 лет. Найти цену облигации, если доходность к погашению (номинальная процентная ставка при условии начисления процентов 2 раза в году) равна 14,47 %.

Решение: Согласно (Error: Reference source not found) цена облигации равна:

Пример 15. Облигация с фиксированным купоном, равным 20% от номинала и выплачиваемым ежегодно, куплена по курсу 90. Срок облигации 10 лет. Найти простую доходность и доходность по приближенной формуле (Error: Reference source not found).

Решение:

, или .

, или .

Отметим, что численное решение уравнения (Error: Reference source not found) приводит к следующему значению для доходности по сложной ставке: i=22,6%. В данном случае лучшим приближением для i является доходность , посчитанная по приближенной формуле (Error: Reference source not found).