
- •4. Модели задач планирования и управления горным производством
- •4.1. Задачи о расстановке оборудования
- •4.2. Задачи об оптимальном использовании ресурсов (оптимальном плане выпуска продукции)
- •4.3. Планирование добычных работ в режиме усреднения качества
- •4.4. Планирование перевозок грузов горных предприятий
- •4.5. Модель задачи планирования работы группы горных предприятий (добывающих и перерабатывающих)
- •4.6. Модели задач размещения
- •4.7. Моделирование организации очистных работ на шахтах
- •4.8. Модель оперативного планирования распределения самоходного оборудования по очистным блокам рудника
- •4.9. Статическая задача распределения ресурсов
- •4.10. Динамическая задача распределения ресурсов
- •4.11. Задачи моделирования процессов и классификация способов взаимодействия машин и механизмов
- •4.12. Моделирование непосредственного взаимодействия машин и механизмов
4.5. Модель задачи планирования работы группы горных предприятий (добывающих и перерабатывающих)
В составе комбината (объединения, подотрасли или отрасли в целом) имеется несколько добывающих и перерабатывающих предприятий. На каждом предприятии добывается полезное ископаемое определенного качества и с определенными затратами на добычу. Имеется несколько перерабатывающих предприятий (потребителей). Технологические и экономические показатели переработки руды каждого типа на перерабатывающих предприятиях известны. Известны затраты на транспорт от горного предприятия к перерабатывающему предприятию и максимальная производственная мощность добывающих и перерабатывающих предприятий. Необходимо так спланировать работу предприятий комбината (определить объемы добычи и переработки по предприятиям и грузопотоки), чтобы прибыль была максимальной.
Введем следующие обозначения:
i - добывающие предприятия (i = 1, 2, .. ., n);
j - перерабатывающие предприятия (j= 1, 2, ..., m);
i - содержание полезного компонента на i-м предприятии;
![]() -
максимально возможный объем добычи на
i-м
предприятии;
-
максимально возможный объем добычи на
i-м
предприятии;
ci - затраты на добычу на i-м предприятии;
![]() -
максимальный объем переработки на j-м
предприятии;
-
максимальный объем переработки на j-м
предприятии;
![]() -
извлечение полезного компонента в
концентрат на j-м
перерабатывающем
предприятии из руды, добытой на i-м
предприятии;
-
извлечение полезного компонента в
концентрат на j-м
перерабатывающем
предприятии из руды, добытой на i-м
предприятии;
![]() -
затраты j-гo
предприятия на обогащение 1 т руды,
добытой
на i-м
предприятии;
-
затраты j-гo
предприятия на обогащение 1 т руды,
добытой
на i-м
предприятии;
![]() -
требуемое минимальное содержание
полезного компонента на
j-м
предприятии;
-
требуемое минимальное содержание
полезного компонента на
j-м
предприятии;
![]() -
допустимое максимальное содержание
полезного компонента
на j-м
предприятии;
-
допустимое максимальное содержание
полезного компонента
на j-м
предприятии;
cij - затраты на транспортирование руды с i-гo рудника на j-ю обогатительную фабрику;
Ц - цена единицы конечной продукции.
Управляемыми переменными в задаче являются:
yi - плановая добыча на i-м предприятии;
yj - плановый объем переработки на j-й обогатительной фабрике;
xij - объем перевозок с i-гo добывающего предприятия на j-ю обогатительную фабрику.
При этом
![]() и
и
![]() (54)
(54)
В данной постановке за критерий оптимальности можно принять прибыль комбината
П = Д - ЗД - ЗТ - ЗО, (55)
где Д - доход комбината; Зд, Зт и ЗО - соответственно затраты на добычу, транспорт и обогащение.
Целевая функция задачи имеет следующий вид:
![]() (56)
(56)
При ограничениях:
а) по объему добычи
![]() (57)
(57)
б) по объему переработки
![]() (58)
(58)
в) по содержанию металла (по качеству)
![]() (59)
(59)
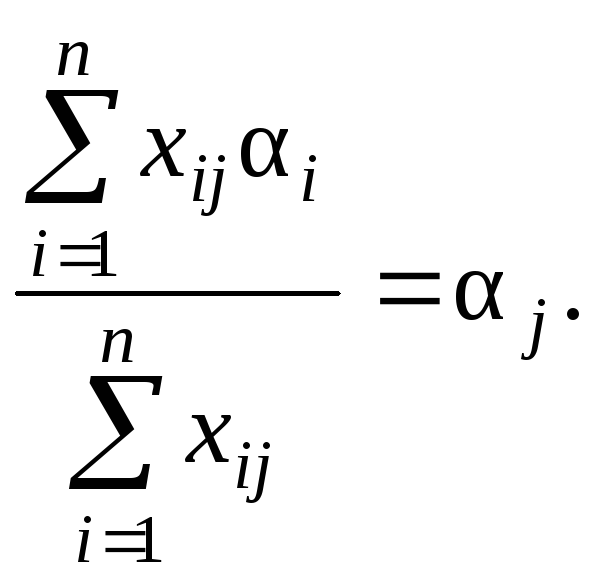
В
простейшем случае, когда i,
ci,
cij,
![]() ,
и
,
и
![]() не зависят от объемов добычи,
переработки и перевозок, задача является
линейной. Если же
эти величины являются функциями
управляемых переменных, то
задача существенно усложняется и
становится нелинейной.
не зависят от объемов добычи,
переработки и перевозок, задача является
линейной. Если же
эти величины являются функциями
управляемых переменных, то
задача существенно усложняется и
становится нелинейной.
