
7Смешанное произведение
.docСмешанное произведение:
О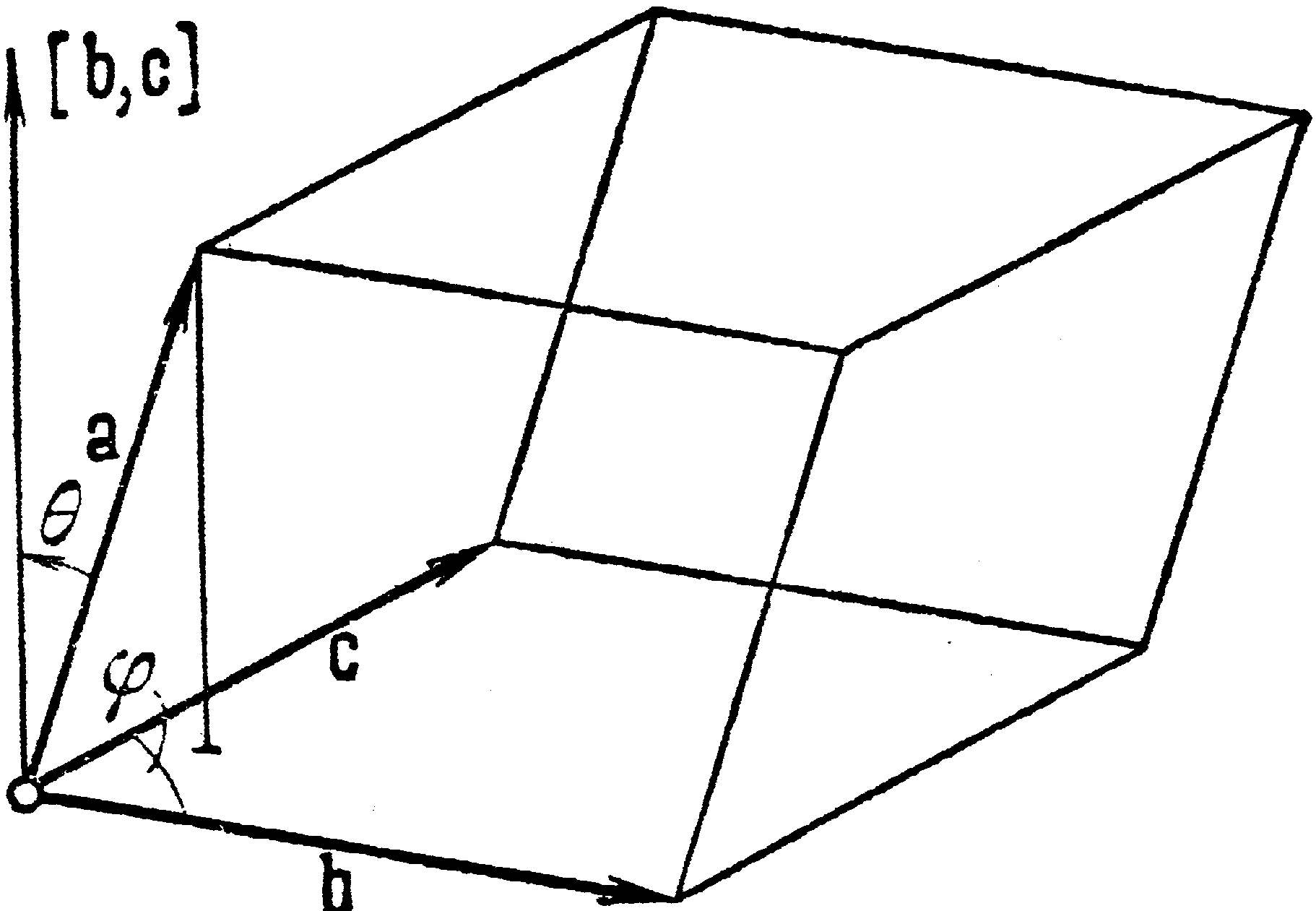 пределение:
Число (а, [b,с])
наз.
смешанным
произведением
векторов
а,b,с и
обозначается (а,b,с).
Предложения:
[1]
Смешанное
произведение некомпланарных векторов
а,b
и с
по модулю равно объему параллелепипеда,
построенного на сомножителях. Оно
положительно, если тройка
а,b,с
правая, и
отрицательно, если она левая. Действительно,
объем
параллелепипеда,
построенного на векторах
а,b и с, равен
(рис) произведению площади основания
|[b, с]|
на высоту
|a| |cos|.
Здесь
– угол
между векторами а и [b,с]. Поэтому мы можем
записать
V=|[b, c]| |a| |cos|
= |(a,[b,с])|
= |(а,b,с)|.
[5]
Смешанное произведение =
0 тогда и
только тогда, когда сомножители
компланарны (рис). Действительно,
(а,b,с)
= |a|
|b,c| cos,
где
–
угол между векторами а
и [b,с]. Равенство
|a| |b,c| cos
= 0 возможно только тогда, когда выполнено
хоть одно из условий:
а)
|a| =
0. Очевидно,
что тогда векторы компланарны;
б)
|[b, с]| =
0. Тогда b
и с
коллинеарны и, => а,
b
и с
компланарны.
в)
cos
= 0. Тогда
вектор а
ортогонален
[b,с], т.е.
компланарен b
и с.
Обратное
утверждение доказывается аналогично:
если а,
b
и с
компланарны и не имеют места случаи а)
и б), то имеет место случай в).
пределение:
Число (а, [b,с])
наз.
смешанным
произведением
векторов
а,b,с и
обозначается (а,b,с).
Предложения:
[1]
Смешанное
произведение некомпланарных векторов
а,b
и с
по модулю равно объему параллелепипеда,
построенного на сомножителях. Оно
положительно, если тройка
а,b,с
правая, и
отрицательно, если она левая. Действительно,
объем
параллелепипеда,
построенного на векторах
а,b и с, равен
(рис) произведению площади основания
|[b, с]|
на высоту
|a| |cos|.
Здесь
– угол
между векторами а и [b,с]. Поэтому мы можем
записать
V=|[b, c]| |a| |cos|
= |(a,[b,с])|
= |(а,b,с)|.
[5]
Смешанное произведение =
0 тогда и
только тогда, когда сомножители
компланарны (рис). Действительно,
(а,b,с)
= |a|
|b,c| cos,
где
–
угол между векторами а
и [b,с]. Равенство
|a| |b,c| cos
= 0 возможно только тогда, когда выполнено
хоть одно из условий:
а)
|a| =
0. Очевидно,
что тогда векторы компланарны;
б)
|[b, с]| =
0. Тогда b
и с
коллинеарны и, => а,
b
и с
компланарны.
в)
cos
= 0. Тогда
вектор а
ортогонален
[b,с], т.е.
компланарен b
и с.
Обратное
утверждение доказывается аналогично:
если а,
b
и с
компланарны и не имеют места случаи а)
и б), то имеет место случай в).
