
- •Оглавление
- •Введение
- •1. Аналитическая геометрия и линейная алгебра.
- •Занятие № 5. Линейные пространства.
- •Занятие № 6. Евклидовы пространства.
- •Занятие № 7. Линейные операторы и матрицы.
- •Занятие № 10. Скалярное произведение векторов.
- •Занятие № 11. Векторное и смешанное произведение векторов.
- •Занятие № 12. Прямая на плоскости.
- •Занятие № 13. Кривые второго порядка.
- •Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.
- •Занятие № 15. Плоскость в пространстве.
- •Занятие № 16. Прямая в пространстве.
- •Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
- •Занятие № 18. Поверхности в пространстве.
- •2. Введение в математический анализ.
- •21.3. Доказать, что последовательность
- •4. Интегральное исчисление функций одной переменной.
- •5. Дифференциальное исчисление функций нескольких переменных.
- •Занятие № 46. Пределы и непрерывность функции нескольких переменных.
- •Занятие № 47. Частные производные и дифференциалы.
- •Занятие № 48. Касательная плоскость и нормаль к поверхности.
- •Занятие № 49. Производная по направлению. Градиент.
- •6. Интегральное исчисление функций нескольких переменных. Занятие № 53. Двойные интегралы.
- •7. Ряды.
- •8. Обыкновенные дифференциальные уравнения.
- •19.1. A); б); в); г). 19.2. А); б); в); г). 19.3. А) четная; б) общего вида; в) нечетная.
- •27.4. Касательная , нормаль . 27.5.
- •Рекомендуемая литература
Занятие № 16. Прямая в пространстве.
16.1. Написать канонические уравнения прямой:
1) проходящей через две точки A(1,-1,3), B(2,1,-1),
2)
проходящей через точку A(3,1,2) и параллельной
вектору
![]() .
.
16.2. Найти косинус угла между прямыми:
![]() и
и
![]() .
.
16.3.
Найти расстояние точки M(2,-1,3) до прямой
![]() .
.
16.4. Составить канонические уравнения прямой, проходящей через точку Р(2, -5, 3)
и
параллельной прямой
![]() .
.
16.5
Написать уравнения прямой
![]() в канонической и параметрической
формах.
в канонической и параметрической
формах.
16.6. Даны вершины треугольника A(3,-1,-1), B(1,2,-7) и С(-5,14,-3). Составить канонические уравнения биссектрисы его внутреннего угла при вершине B.
16.7.
Составить уравнения прямой, которая
проходит через точку А(-1,-3,2) и пересекает
две прямые
![]()
![]() ;
;
![]() .
.
16.8.
Исследовать взаимное расположение
прямых
![]() и
и
![]() .
Если прямые пересекаются, то определить
координаты их точки пересечения:
.
Если прямые пересекаются, то определить
координаты их точки пересечения:
а)
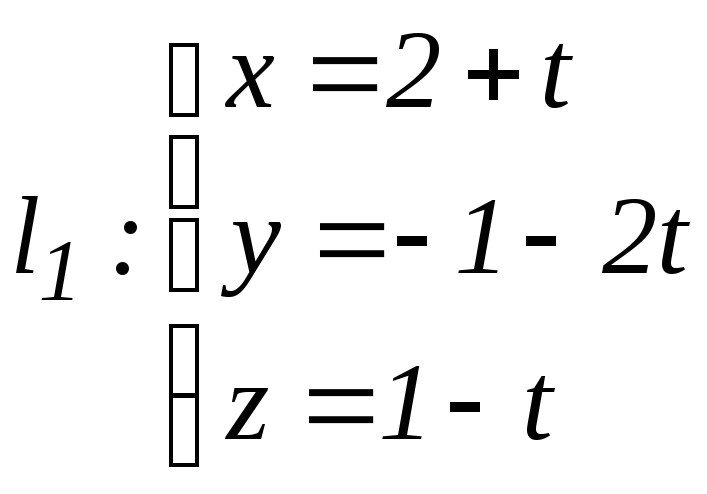 ,
,
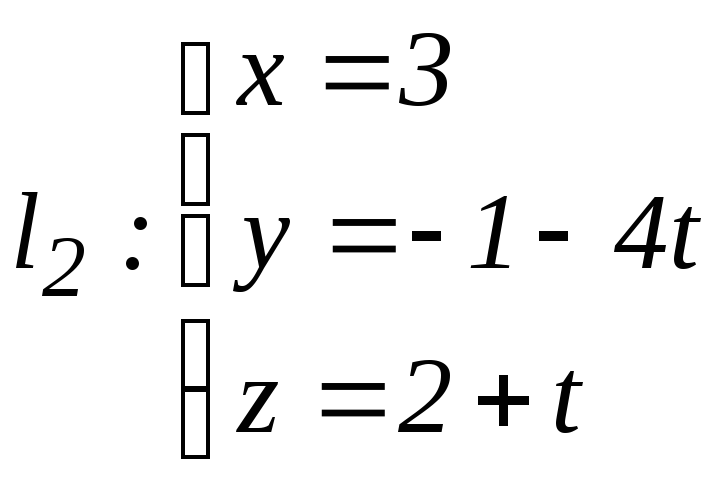 ;
;
б)
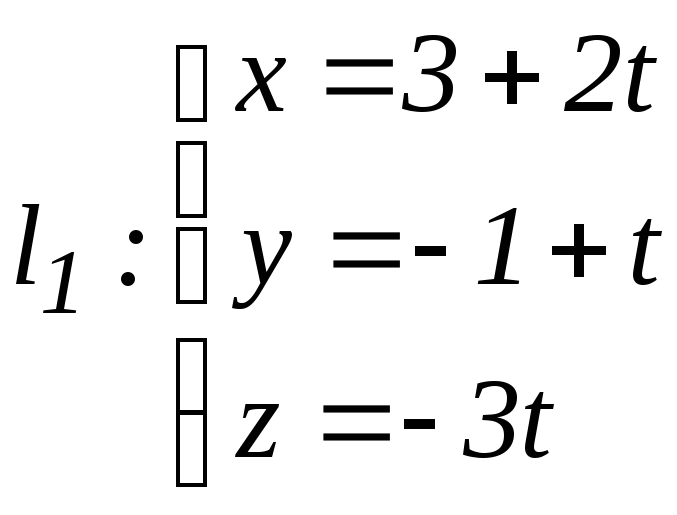 ,
,
![]() ;
;
в)
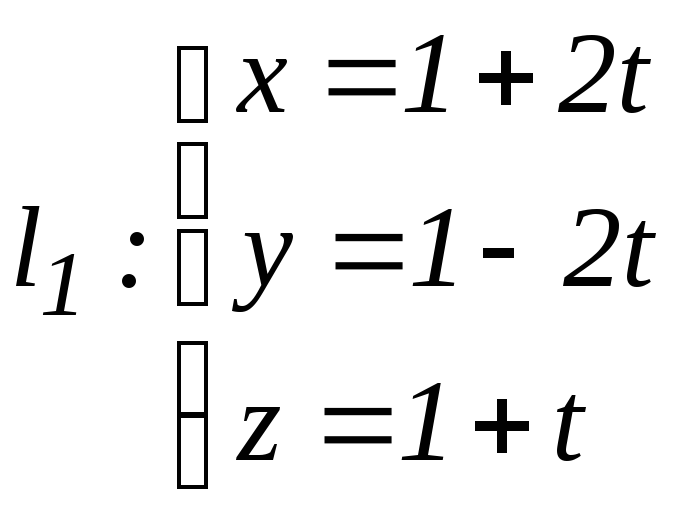 ,
,
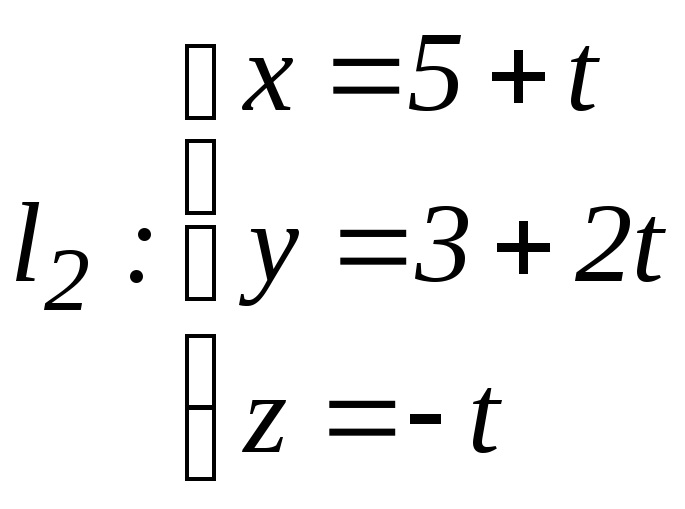 ;
;
г)
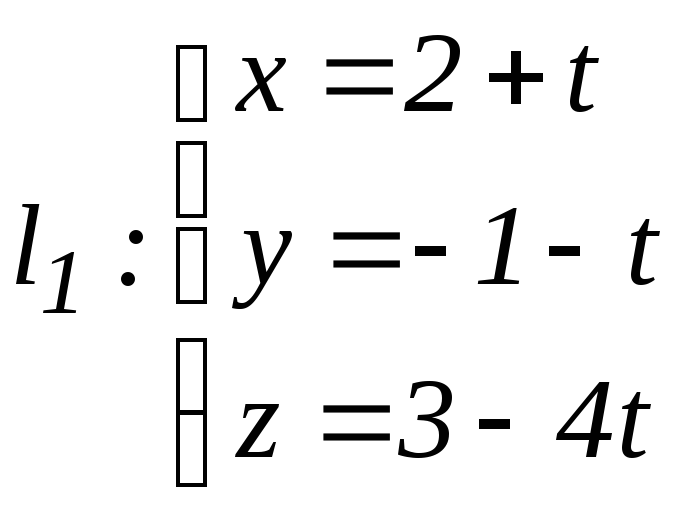 ,
,
![]() .
.
16.9.
Доказать, что прямые
![]() и
и
![]() пересекаются,
и составить уравнение плоскости, которая
их содержит:
пересекаются,
и составить уравнение плоскости, которая
их содержит:
а)
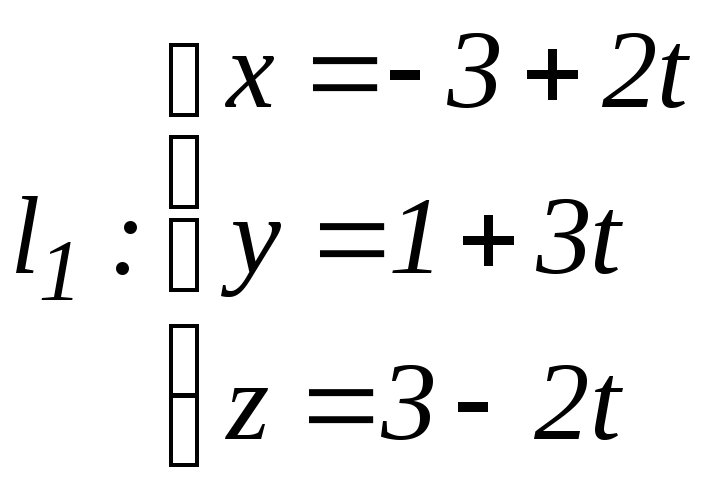 ,
,
![]() ;
;
б)
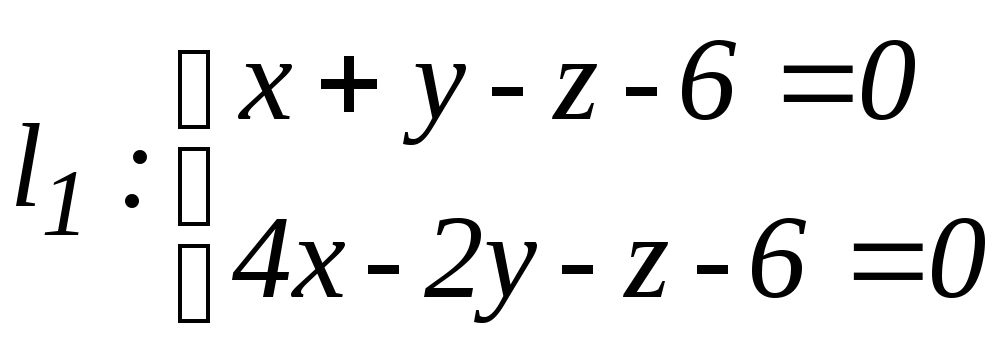 ,
,
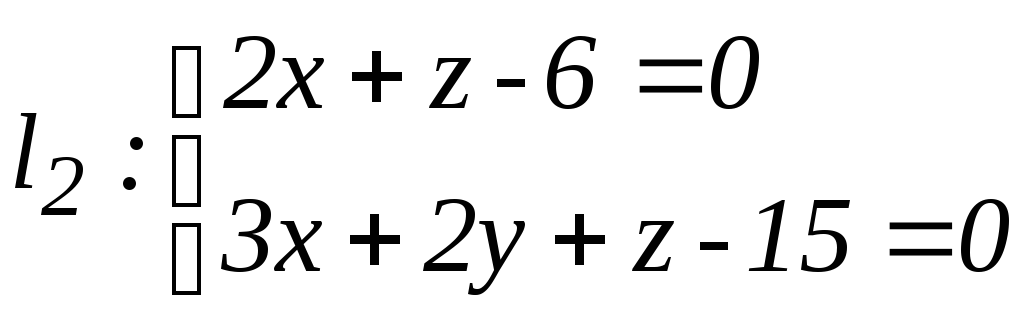 .
.
16.10.
Доказать, что прямые
![]() и
и
![]() скрещиваются.
Составить уравнения плоскостей, каждая
из которых содержит одну из этих прямых
и параллельна второй:
скрещиваются.
Составить уравнения плоскостей, каждая
из которых содержит одну из этих прямых
и параллельна второй:
а)
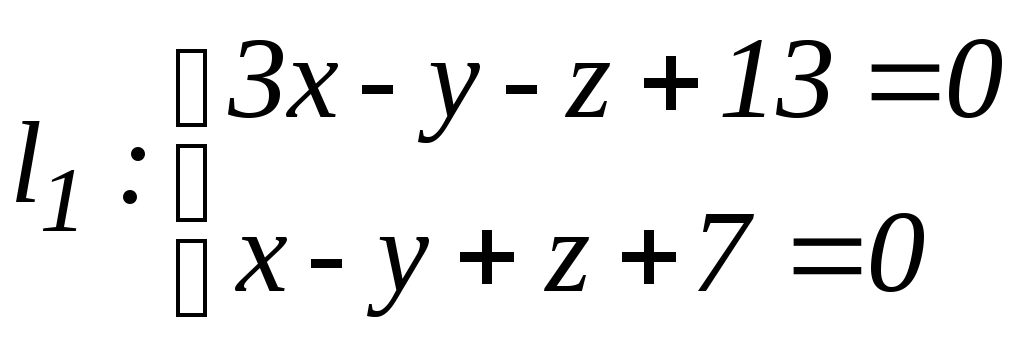 ,
,
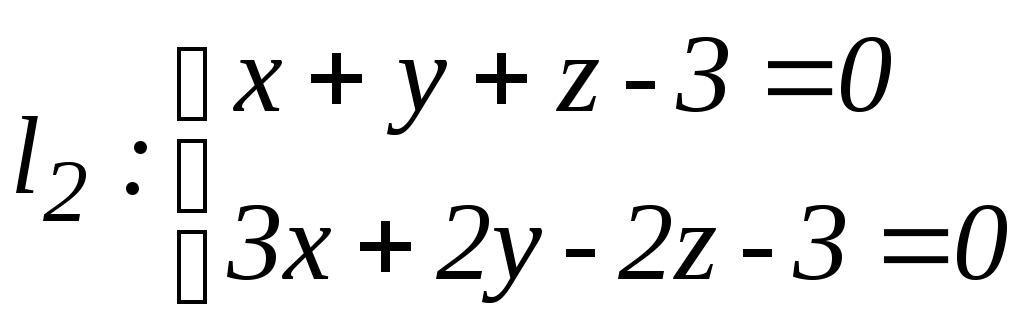 ;
;
б)
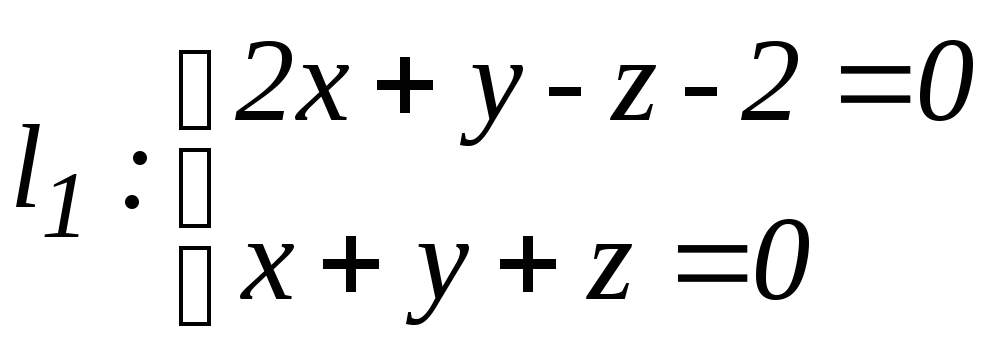 ,
,
![]() .
.
16.11.
Определить уравнение прямой, проходящей
через точку М, пересекающей прямую
![]() и перпендикулярной к ней:)
и перпендикулярной к ней:)
а)
![]()
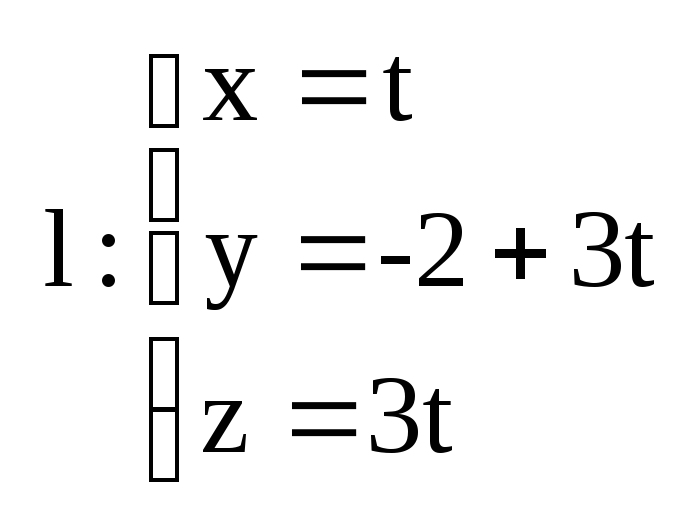
б)
![]()
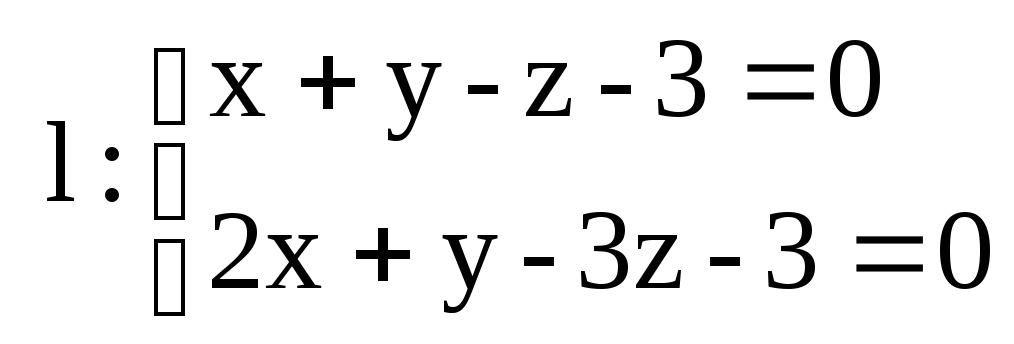
16.12. Даны координаты вершин треугольника АВС. Составить уравнения его высот:
а)
![]()
![]()
![]()
б)
![]()
![]() ,
,
![]()
Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
17.1. Найти точку пересечения прямой и плоскости
![]()
17.2.
Найти проекцию точки М(1,0,-1) на прямую
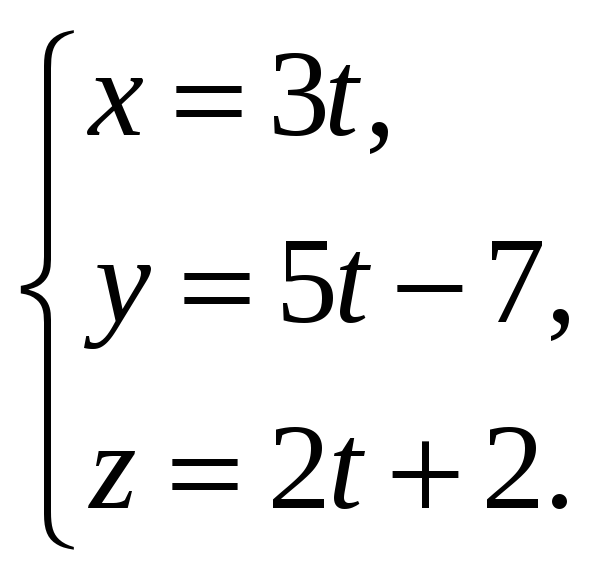
17.3.
Найти проекцию точки М(-1,-2,3) на прямую
![]() .
.
17.4. Найти проекцию точки М(1,1,1) на прямую, проходящую через точки
А(2,5,-3) и В(3,-2,2).
17.5.
Найти проекцию точки М(5,2,-1) на плоскость
![]() .
.
17.6.
Найти точку А,
симметричную точке В(2,-5,7) относительно
прямой, проходящей через точки
![]() (5,
4, 6) и
(5,
4, 6) и
![]() (-2,
-17, -8).
(-2,
-17, -8).
17.7. Найти точку А, симметричную точке B(1,2,3) относительно прямой:
![]()
17.8.
Составить уравнение плоскости, проходящей
через точку А(1, 1, 1) параллельно прямым
![]() и
и
![]() .
.
17.9.
Составить уравнение плоскости,
проходящей через прямую
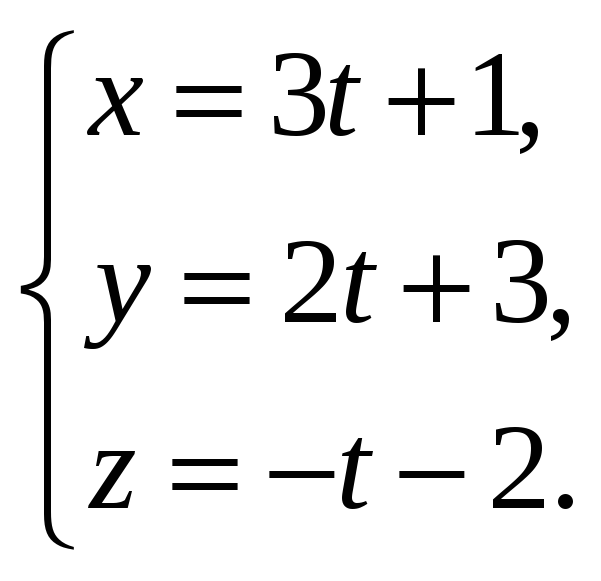 параллельно прямой
параллельно прямой
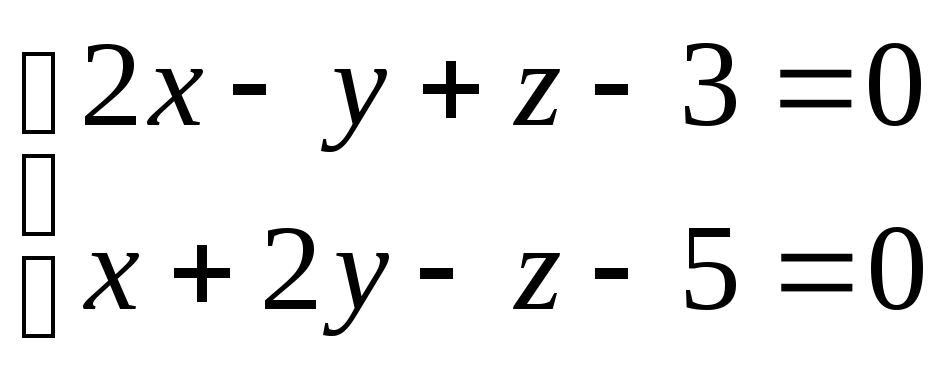 .
.
17.10.
Составить уравнение плоскости,
проходящей через прямую
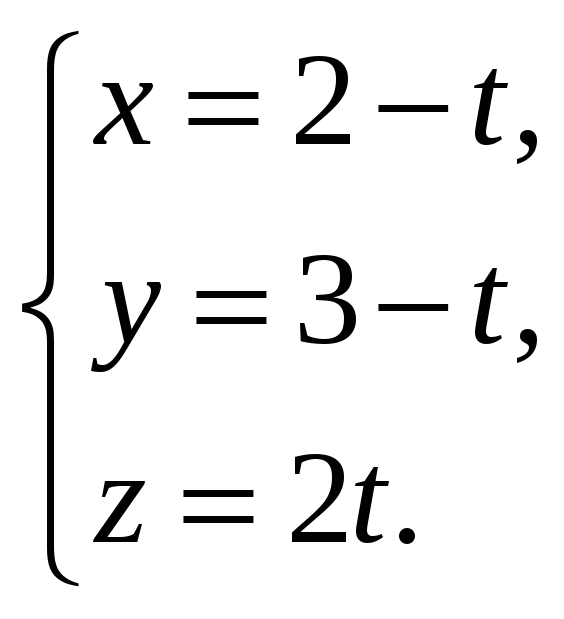 и точку Р(0, 0, 0).
и точку Р(0, 0, 0).
17.11.
Доказать, что прямые
![]() и
и
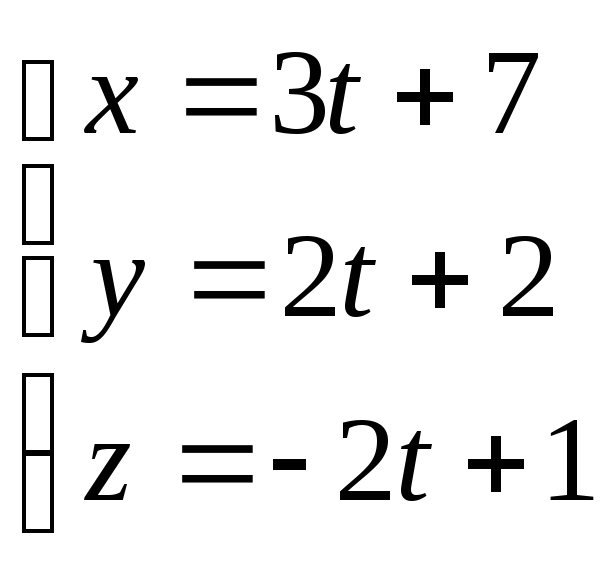 лежат в одной плоскости и составить ее
уравнение.
лежат в одной плоскости и составить ее
уравнение.
17.12.
Найти уравнения прямой, проходящей
через точку М(3,-2,4) параллельно плоскости
![]() и пересекающей прямую
и пересекающей прямую
![]() .
.
17.13.
Написать канонические уравнения прямой,
образованной пересечением плоскости
![]() с плоскостью Oyz.
с плоскостью Oyz.
17.14.
Найти расстояние между прямыми
![]() и
и
![]() .
Составить уравнение плоскости, проходящей
через эти прямые.
.
Составить уравнение плоскости, проходящей
через эти прямые.
Занятие № 18. Поверхности в пространстве.
18.1. Определить тип поверхности второго порядка при различных значениях параметра k:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
18.2.
Составить уравнение сферы с центром в
точке А(1,1,1) и радиусом
![]() .
.
18.3. Найти координаты центра А и радиус сферы R:
а)
![]() ;
;
б)
![]() .
.
18.4. Найти координаты центра поверхности и вершин, ее полуоси и уравнения плоскостей симметрии, оси симметрии, изобразить поверхность в исходной системе координат:
а)
![]() ;
;
б)
![]() .
.
18.5. Определить тип поверхности:
а)![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
18.6. Определить тип поверхности:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)![]() .
.
