Занятие № 13. Кривые второго порядка.

13.1. Составить уравнение окружности, касающейся двух параллельных прямых: , , причем одной из них – в точке А(2, 1).

13.2. Составить уравнение окружности, касающейся осей координат, если центр окружности лежит в точке с координатами .

13.3. Дана окружность . Из ее точки А(2,0) проведены всевозможные хорды. Определить геометрическое место середин этих хорд.

13.4. Дан эллипс найти:

1. его полуоси,

2. фокусы,

3. эксцентриситет,

4. уравнение директрис.

13.5. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что

1) его полуоси равны 3 и 2;

2) его малая ось равна 24, а расстояние между фокусами 2с=10.

3) его большая ось равна 20, а расстояние между фокусами 2с=12,

4) его малая полуось равна 10, а эксцентриситет ,

5) его большая ось равна 20, а эксцентриситет .

6) расстояние между его директрисами равно 10 и расстояние между фокусами 2с=8,

7) его большая ось равна 8, а расстояние между директрисами равно 16,

8) его малая ось равна 4 расстояние между директрисами равно 10,

9) расстояние между его директрисами равно 16 и .

13.6. Найти острый угол между асимптотами гиперболы .

13.7. Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс, симметрично относительно начала координат, зная, что

1) ее оси 2а=4 и 2b=6,

2) расстояние между фокусами 2с=16 и ось 2b=12,

3) расстояние между фокусами 2с=6 и эксцентриситет ,

4) расстояние между директрисами равно и расстояние между фокусами 2с = 26;

5) расстояние между директрисами равно и эксцентриситет ;

6) расстояние между директрисами равно , а уравнения асимптот имеют вид .

13.8. Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси и ее параметр р=3.

13.9. Составить уравнение параболы, которая имеет фокус F (0,-3) и проходит через начало координат, зная, что ее осью служит ось .

13.10. Найти координаты фокуса параболы:

1. ;

2. ,

3. ;

4. .

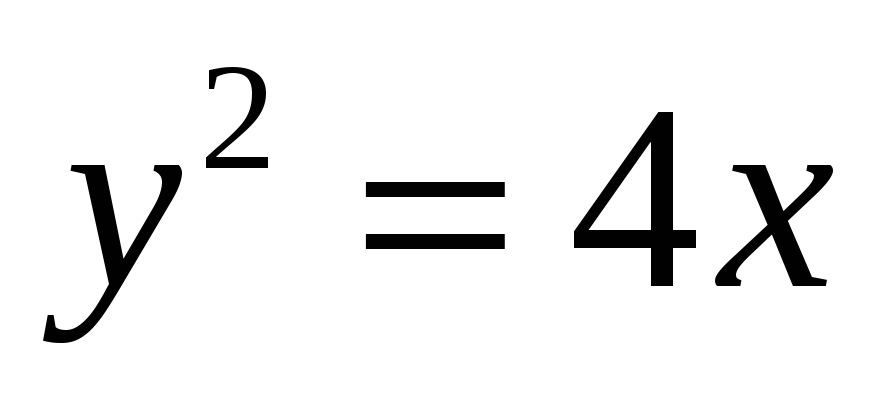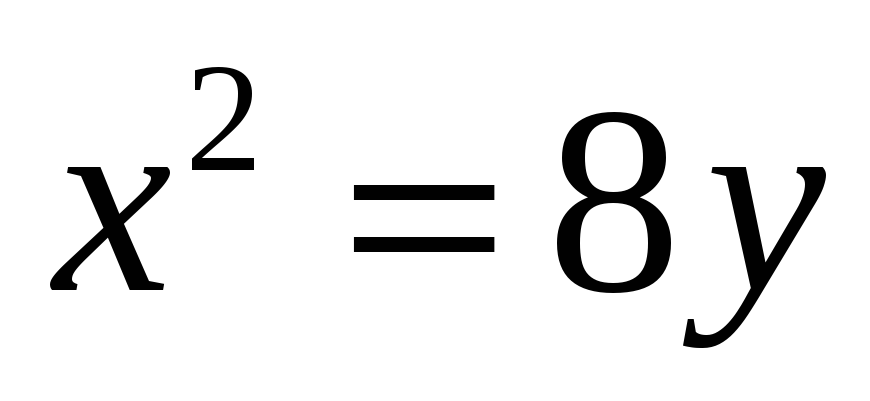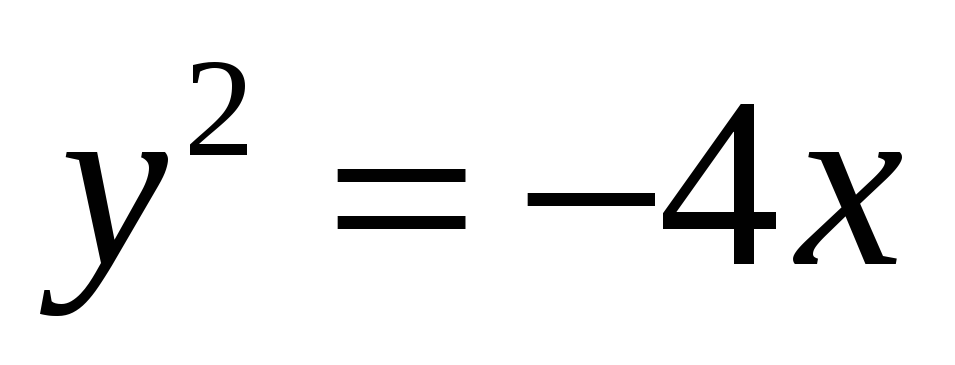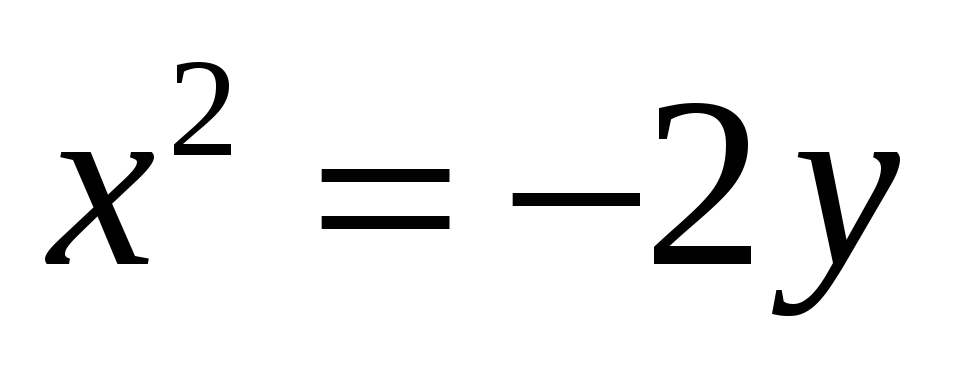13.11. Найти вершину, фокус, ось и директрису параболы .

Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.

14.1. Определить тип кривой второго порядка, составить ее каноническое уравнение:

1) ;

2) ;

3) ;

4);

5) ;

6) .

14.2. Определить тип кривой приведением ее уравнения к каноническому виду методом Лагранжа:

1) ;

2) ;

3) ;

4) ;

5) .

14.3. Определить тип кривой методом инвариантов:

1) ;

2) ;

3) ;

4) ;

5) .

14.4. Составить уравнение линии, сумма расстояний точек которой до точек А (2,4) и

В (-4,4) равна 8.

14.5. Составить уравнение линии, каждая точка которой вдвое дальше от прямой , чем от точки Р.

Занятие № 15. Плоскость в пространстве.

15.1. Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор

15.2. Найти угол между плоскостями 3x – y + 2z + 15 = 0 , 5x + 9y – 3z – 1 = 0

15.3. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору : A(1, 0, -2), B(2, -1, 3 ), C(0, -3, 2)

15.4. Найти уравнение плоскости, проходящей через точки А(5, 4, 1), В(4, -2, -1), С(0, 6, 5).

15.5. Составить уравнение плоскости, проходящей через точку Р параллельно двум векторам , .

15.6. Составить уравнение плоскости, проходящей через начало координат и перпендикулярной к плоскостям x +2y – 2z = 1, x – 2y + z = 4.

15.7. Найти расстояние от точки М(1,3,1) до плоскости 2x – y – 2z – 3 = 0.

15.8. Написать уравнение плоскости, проходящей через точку Р(3,-1,-2) и отсекающей на осях координат равные отрезки.

15.9. Написать уравнение плоскости, проходящей через точку M(1,0,2) и отсекающей на осях Ox и Oy отрезки a=2 и b=3.

15.10. Найти косинусы углов нормали плоскости 2x + y + 2z – 4 = 0 с осями координат.

15.11. Написать уравнение плоскости, проходящей через ось Oz и через точку А(2;1;-1). 15.12. Вычислить расстояние от точки (-1, 1, -2) до плоскости, проходящей через три точки А(1, -1, 1), В(-2, 1, 3), С(4, -5, -2).

15.13. Составить уравнения плоскостей, параллельных плоскости и отстоящих от нее на расстояние d = 5.

15.14. Тетраэдр задан координатами своих вершин: Составить уравнения плоскостей, проходящих через: а) вершину D, параллельно грани ABC; б) вершину В, параллельно грани ADC; в) ребро АС, параллельно ребру BD; г) ребро ВС, параллельно ребру AD.

15.15. Даны координаты четырех вершин параллелепипеда :

Составить уравнения плоскостей, проходящих через:

а) ребро , параллельно диагонали ;

б) диагональ грани, параллельно диагонали ;

в) диагональ грани, параллельно прямой .