Занятие № 5. Линейные пространства.

5.1. Являются ли следующие системы векторов линейно независимыми:

а) ;

б) ;

в)

г) .

5.2. Вычислить ранги систем векторов:

а)

б)

в)

5.3. В некотором базисе заданы векторы

Найти разложение вектора b по базису

5.4. Разложить вектор по базису

5.5. Выразить координаты вектора в новом базисе через координаты в старом базисе, если старый базис , а новый базис

5.6. Разложить вектор по базису с применением матрицы перехода от одного базиса к другому.

5.7. Найти размерность и базисы линейных подпространств, натянутых на системы векторов:

а)

б)

5.8. Найти базис подпространства, заданного системой уравнений:

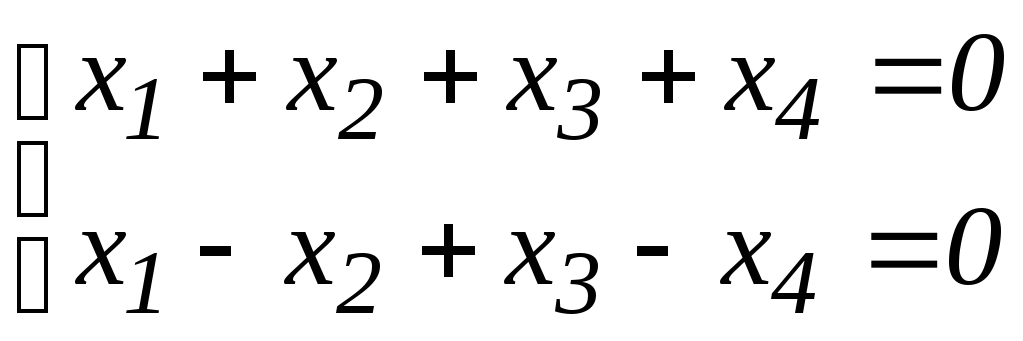
5.9. Найти базис подпространства, заданного уравнением .

5.10. Найти систему линейных уравнений, задающую линейное подпространство, содержащие векторы:

а)

б)

Занятие № 6. Евклидовы пространства.

6.1. Проверить, что векторы и попарно ортогональны и достроить их до ортогонального базиса.

6.2. Проверить, что векторы и попарно ортогональны и достроить их до ортогонального базиса.

6.3. Найти векторы, дополняющие следующие системы векторов до ортонормированных базисов:

а)

б)

6.4. Применяя процесс ортогонализации и нормирование векторов, ортонормировать систему векторов:

а)

б) ,

6.5. Подпространство L евклидова пространства задано в некотором ортонормированном базисе системой линейных уравнений. Найти хотя бы один ортонормированный базис в L:

а) ; б) ;

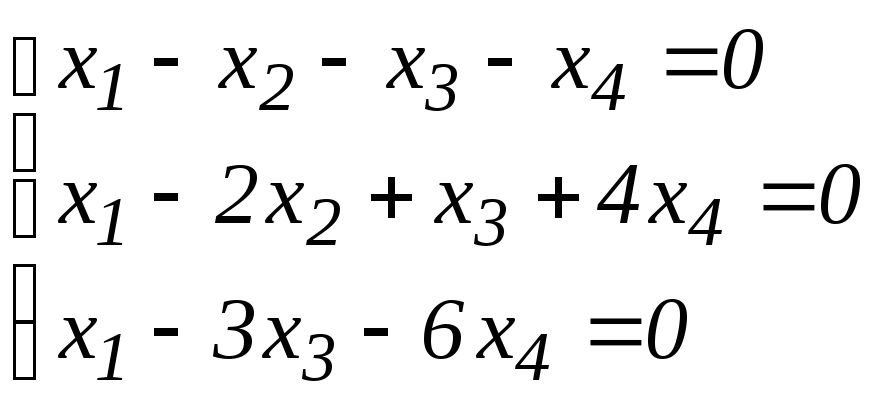в) .

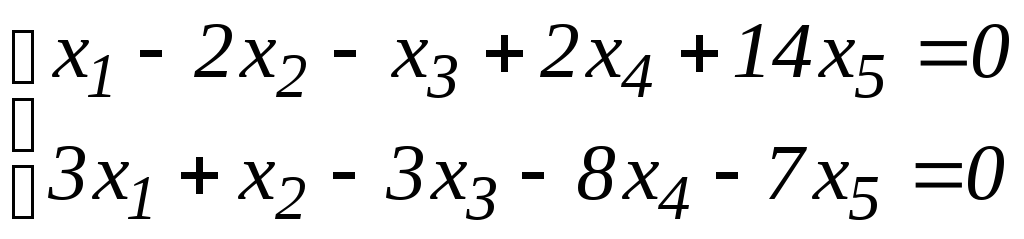Занятие № 7. Линейные операторы и матрицы.

7.1. Линейный оператор трехмерного линейного пространства задан в стандартном базисе матрицей

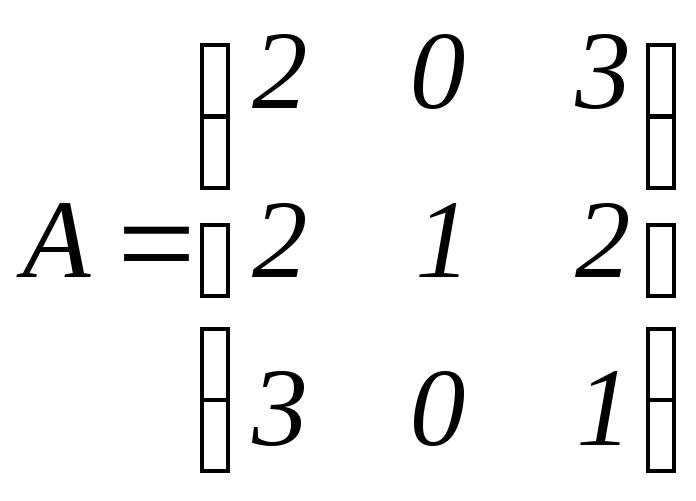
Найти образы следующих векторов:

7.2. Линейный оператор L двумерного векторного пространства переводит векторы

в векторы Вычислить матрицу оператора L в стандартном базисе.

7.3. Линейный оператор L имеет в данном базисе матрицу

,

а координатные столбцы новых базисных векторов образуют матрицу

.

Вычислить матрицу преобразования в новом базисе.

7.4. Линейный оператор L имеет в данном базисе матрицу

,

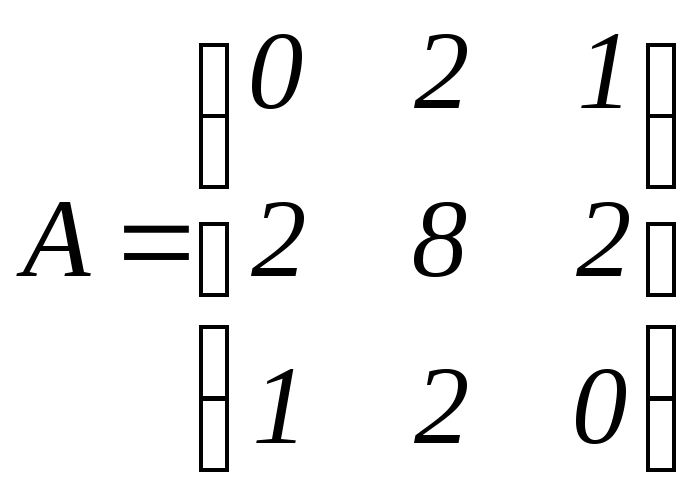а координатные столбцы новых базисных векторов образуют матрицу

.

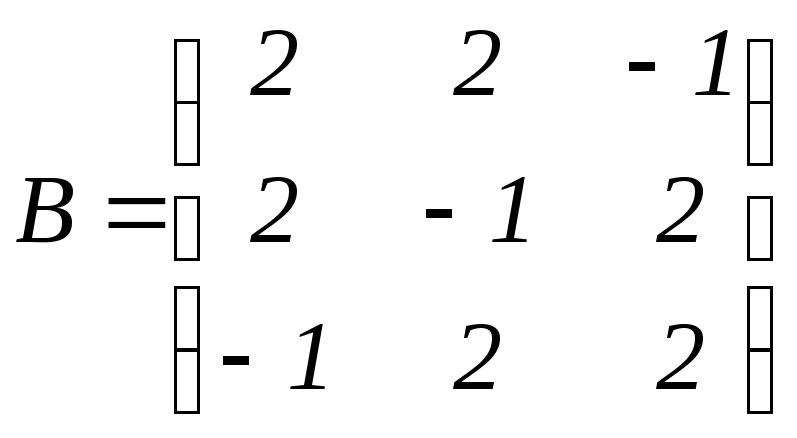Вычислить матрицу преобразования в новом базисе.

7.5. Найти собственные значения и собственные векторы линейных операторов, заданных в некотором базисе матрицами:

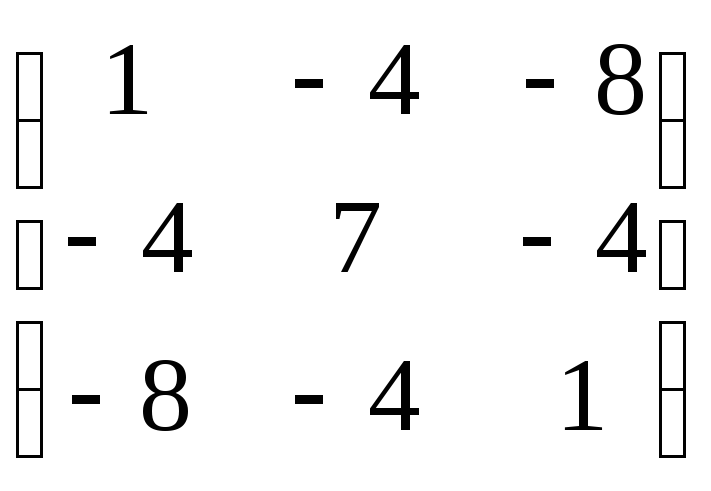а) б) в) г) д) .

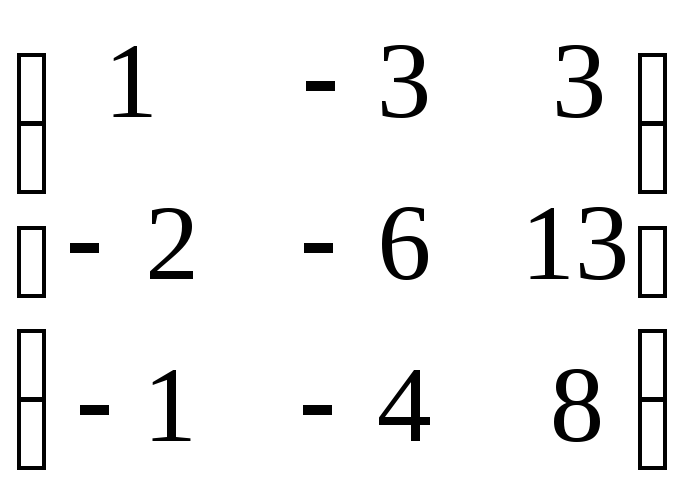Занятие № 8.

Квадратичные формы.

8.1. Записать квадратичную форму в матричном виде:

а) ;

б)

8.2. Привести к каноническому виду квадратичную форму:

а) ;

б) ;

в) ;

г) ;

д) ;

е)

8.3. Найти линейное преобразование, переводящее квадратичную форму f(x) в квадратичную форму g(y):

а) ;

;

б) ;

;

в) ;

.

Занятие № 9.

Векторы и линейные операции над ними.

9.1. В треугольнике АВС медианы пересекаются в точке М. Доказать:

а) ; б) для любой точки О выполняется равенство: .

9.2. Дан треугольник АВС, О – точка пересечения его медиан, М,Р и Q – середины сторон АВ, ВС и АС соответственно. Найти координаты векторов АВ, ВС и АС в базисе .

9.3. Выяснить, является ли система векторов базисом плоскости. Если является, то найти координаты вектора в этом базисе.

9.4. Выяснить, образуют ли векторы базис пространства. Если да, то найти координаты вектора относительно этого базиса.

9.5. Выяснить, компланарны ли векторы Если компланарны, то найти координаты вектора в базисе .

9.6. Доказать, что точки лежат на одной прямой.

9.7. Доказать, что четырехугольник с вершинами

является трапецией.

9.8. Даны координаты четырех вершин параллелепипеда . Определить координаты остальных вершин:

а)

б)

в)

9.9. Даны координаты вершин треугольника АВС. Найти координаты точки пересечения биссектрисы угла А со стороной ВС:

а)

б)

9.10. Даны координаты двух смежных вершин квадрата. Найти его площадь:

а) ;

б)

9.11. Даны две координаты вектора : y=4; z=-12. Определить его первую координату x при условии, что .

9.12. Дан модуль вектора и углы, образованные с осями координат: α=135º; β=120º; γ=60˚. Найти проекции вектора на координатные оси.

9.13. Определить координаты вектора , составляющего с осями координат равные углы при условии, что .

9.14. Написать разложение вектора по векторам , , :

9.15. Написать разложение вектора по векторам , , :

9.16. Выяснить являются ли векторы и линейно зависимыми?

9.17. Коллинеарны ли векторы и , построенные по векторам и ?

a)

b)

9.18. Найти координаты точки А, делящей отрезок в отношении , если , .