Контрольные вопросы

1. Какова цель данной работы?

2. Записать и сформулировать второй закон Ньютона в общем виде и в классической механике.

3. Что называется силой? Единица измерения силы.

4. Как определяется в данной работе сила, под действием которой движется вся система?

5. Каков физический смысл массы тела? Единица измерения.

6. Как определить массу движущейся системы в данной работе?

7. Изменяется ли движущая сила в случае двух дополнительных грузов на одном грузе и на разных грузах? Изменяется ли при этом масса движущейся системы?

8. Дать определение перемещения, пути, скорости, ускорения. Единицы их измерений.

9. Записать кинематические формулы пути и скорости. По какой формуле вычисляется ускорение в данной работе?

10. От каких величин зависит ускорение?

11. Почему в данной работе ускорение движущейся системы не равно ускорению свободного падения?

12. Как в данной работе проверяется второй закон Ньютона?

Лабораторная работа № 2

«Проверка основного закона динамики

Вращательного движения»

Цель работы: с помощью маятника Обербека проверить опытным путем соотношение величин при вращательном движении.

Приборы и принадлежности:

1. Маятник Обербека.

2. Набор грузов.

3. Измерительная линейка.

4. Секундомер.

Краткая теория

Вращательным движением абсолютно твердого тела называется такое движение, при котором все точки тела описывают концентрические окружности с центрами, лежащими на одной прямой, называемой осью вращения.

Движение любой точки тела по окружности характеризуется следующими кинематическими величинами:

- угловой путь - это угол поворота радиуса вращения за время t; .

- угловая скорость - определяет изменение углового пути за единицу времени; .

- угловое ускорение – определяет изменение угловой скорости за единицу времени; .

Все эти величины одинаковы для каждой точки абсолютно твердого тела и не зависят от расположения точки относительно оси вращения тела. Вектор угловой скорости направлен по оси вращения согласно правилу правого винта (рис. 1). Вектор углового ускорения направлен также вдоль оси вращения в соответствии со знаком изменения углового ускорения (рис. 1).

Между линейными и угловыми величинами существует связь через радиус вращения материальной точки .

Линейный путь , то есть длина дуги окружности радиуса :

; (1)

линейная скорость:

; (2)

касательное ускорение:

; (3)

центростремительное ускорение:

. (4)

Опыт показывает, что изменение вращательного движения зависит не только от величины приложенной к нему силы, но и от точки приложения силы и направления ее действия. Для характеристики способности силы вызывать изменение вращения вокруг данной оси вводится понятие о моменте сил относительно оси.

Моментом силы относительно оси вращения называется векторное произведение радиуса – вектора , проведенного из точки О в точку приложения силы , на вектор силы :

.

Вектор всегда перпендикулярен плоскости, в которой лежат вектора и , то есть направлен вдоль оси вращения (направление определяется по правилу векторного произведения, или по правилу правого винта, или по правилу обхвата правой руки) (рис. 2, а).

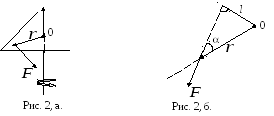
Численное значение момента силы (рис. 2, б) , где - угол между векторами и . Из рис. 2, б , - плечо силы - _{кратчайшее расстояние от оси вращения до линии действия силы. Таким образом,}

₍₅₎

_{Если направление действия силы параллельно оси вращения или пересекает ее, то такая сила не может изменить вращательное движение, так как в этих случаях момент силы .}

_{Основным уравнением динамики вращательного движения является второй закон Ньютона, примененный к угловым характеристикам:}

_{, (6)}

_{где - главный момент всех внешних сил, действующих на тело;}

_{- угловое ускорение;}

_{- момент инерции тела относительно оси вращения.}

_{Момент инерции есть мера инертности вращающегося тела относительно данной оси вращения.}

_{Момент инерции материальной точки , где - масса материальной точки, - радиус вращения материальной точки.}

_{Момент инерции тела зависит от распределения массы тела относительно оси вращения.}

_{Момент инерции твердого тела равен сумме моментов инерции всех материальных точек, составляющих это тело:}

_.

_{Таким образом, формулировка основного закона динамики вращательного движения следующая:}

_{угловое ускорение , полученное вращающимся телом, прямо пропорционально суммарному (главному) моменту сил} , действующих на это тело, и обратно пропорционально моменту инерции тела _.

В лабораторной работе требуется проверить на опыте выполнение этого закона.

Согласно выражению (6) при постоянном значении момента силы (), но при разных значениях момента инерции _тела:

_,

_{отсюда при} (7)

При постоянном моменте инерции (), но при разных значениях моментов сил имеем:

.

Тогда при (8)

Соотношения (7) и (8) необходимо проверить в лабораторной работе.