Описание установки

Для исследования зависимости мощности и КПД электрической цепи от величины силы тока, будем пользоваться электрической цепью, собранной по схеме (рис. 1).

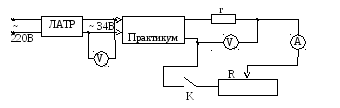
Рис. 1.

Выполнение работы

1. Собрать электрическую цепь по схеме (см. рис. 1) и предъявить для проверки преподавателю.

2. Измерить ЭДС источника вольтметром V₁ при разомкнутом ключе.

3. При полностью введенном реостате замкнуть ключ. Измерить силу тока и напряжение.

4. Меняя сопротивление реостата, увеличивать силу тока и снять 8-10 значений силы тока и соответствующих им значений напряжения.

5. Измерить ток при напряжении, равном половине ЭДС источника, чтобы получить вершину параболы.

6. Вычислить для всех точек полную мощность, полезную мощность по формулам , и КПД источника по формуле .

7. Данные измерений и вычислений занести в таблицу 1.

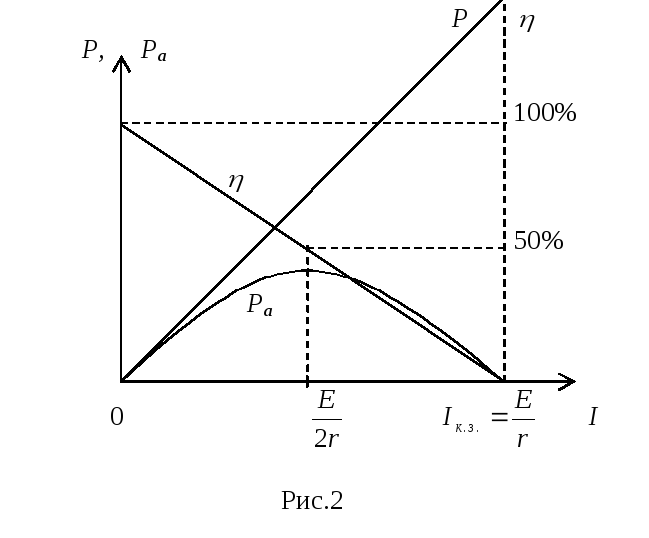
8. Построить графики полной и полезной мощностей и КПД источника в зависимости от силы тока.

Для полной и полезной мощностей выбрать одинаковый масштаб.

Таблица 1

№ п/п	Данные измерений			Результаты вычислений
	Е, В	I, A	Ua, B	P, Bт	Ра, Вт	η

Контрольные вопросы

1. Записать закон Ома для однородного участка цепи и закон Ома для полной цепи.

2. Что называется ЭДС источника тока? Как измерить ЭДС?

3. Записать формулы работы и мощности постоянного тока.

4. Записать формулы мощности электрического тока и мощности источника тока.

5. Вывести формулу зависимости полезной мощности от силы тока в цепи.

6. Вывести формулу зависимости КПД электрической цепи от силы тока.

7. Можно ли получить КПД электрической цепи 100 %?

8. При каком значении КПД полезная мощность максимальна? Чему равно значение силы тока?

9. Что называется коротким замыканием?

Лабораторная работа № 12 «Экспериментальная проверка закона полного тока»

Цель работы: экспериментально подтвердить справедливость закона полного тока.

Приборы и принадлежности:

1. Большая катушка

2. Амперметр

3. Баллистический гальванометр

4. Переключатель

5. Источник электрического тока

6. Малая катушка

Краткая теория

Как показывает опыт, в пространстве, окружающем неподвижные электрические заряды, возникает электростатическое поле, а в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным.

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Отличительная особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды.

Так как магнитное поле является силовым, то его по аналогии с электрическим графически изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора магнитной индукции . Их направление определяется правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

Физическое толкование магнитной индукции можно дать из закона Ампера:

.

Если угол между и равен , то .

Тогда

,

откуда

.

Магнитная индукция В численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, по которому течет ток единичной силы и который расположен перпендикулярно к направлению поля.

характеризует силовое действие магнитного поля на движущийся электрические заряды (токи0 и является аналогом напряженности электрического поля , которая характеризует силовое действие электрического поля на заряд в данной точке поля.

Наряду с для описания магнитного поля в вакууме вводится величина , называемая напряженностью магнитного поля (аналог ).

В случае однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

,

где ₀ – магнитная постоянная; .

 – безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков среды, .

Таким образом, если известна величина индукции магнитного поля , то легко может быть рассчитана величина напряженности магнитного поля и наоборот. Индукция магнитного поля в ряде случаев может быть рассчитана на основании закона Био-Савара-Лапласа. Однако иногда прямое использование этого закона не позволяет решить задачу. В таких случаях индукция магнитного поля может быть определена с использованием закона полного тока.

Закон полного тока формулируется следующим образом:

Циркуляция вектора напряженности вдоль произвольного замкнутого контура равна алгебраической сумме токов, охватываемых этим контуром.

Математически запись закона полного тока имеет вид:

, (1)

где I_i – значение токов проводимости.

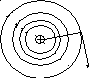
Рассмотрим магнитное поле бесконечно длинного прямолинейного проводника с током I. Линии напряженности магнитного поля этого тока – концентрические окружности, лежащие в плоскости, перпендикулярной проводнику с током (касательные к этим линиям совпадают с вектором ).

I

l

Рис. 1

Циркуляция вектора напряженности этого поля вдоль произвольной силовой линии l (окружности радикса r) равна

.

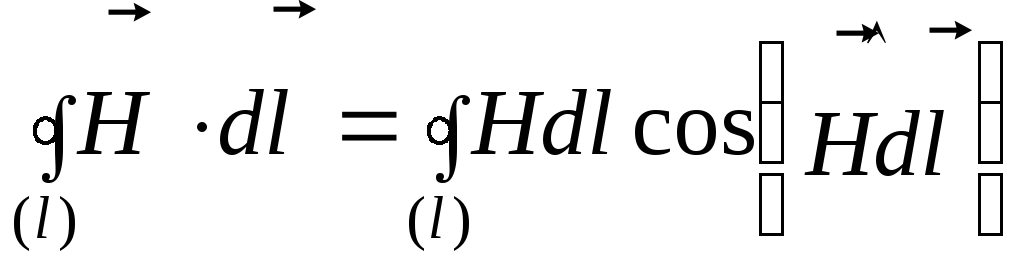Во всех точках окружности l

, ,

следовательно .

Тогда

.

Таким образом

. (2)

Полученный результат верен для проводника с током любой геометрической формы при обходе по замкнутому контуру, охватывающему его.

Если магнитное поле создано системой токов I₁, I₂,…, I_n, то вектор напряженности будет равен геометрической сумме напряженностей полей, создаваемых каждым током в отдельности.

Поэтому формулу (2) можно записать в общем виде:

. (3)

Если контур не охватывает провод с током, то

.

Каждый ток учитывается столько раз, сколько раз он охватывается контуром.

Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта, ток противоположного направления считается отрицательным.

Для экспериментальной проверки закона полного тока (1) поступим следующим образом. Выберем два произвольных контура. Пусть первый охватывает проводники с током, а второй не охватывает их. Разобьем контур на участки конечной длины l_i, определим на каждом участке экспериментальное значение H_i и сосчитаем сумму

.

При обходе контура эта сумма должна равняться сумме токов , величина которых в опыте изменяется. Обход второго контура должен показать, что

.

Форма контуров может быть выбрана любой. Однако в том случае, когда контур прямоугольный, равенство

является наиболее точным. Поэтому в опыте рекомендуется использовать прямоугольный контур обхода.

Для экспериментального определения величины воспользуемся явлением электромагнитной индукции. Маленькую катушку размеры которой м, подсоединим к баллистическому гальванометру. Пусть в какой-нибудь точке пространства напряженность поля изменяется от нуля до некоторого значения . Это происходит в момент, когда подается питание на проводники электрического тока.

Изменение напряженности за время включения t равно Н = Н. Катушка, замкнутая на гальванометр, располагается так, чтобы плоскость ее витков была перпендикулярна вектору . В этом случае

, (4)

где - составляющая вектора напряженности, совпадающая по направлению с вектором . В момент включения (или выключения) тока катушку пронизывает переменный магнитный поток. Его величина изменяется от нуля до , так что изменение магнитного потока равно .

Значение магнитного потока определяется так:

,

где S – площадь витка катушки. Таким образом, величина магнитного потока зависит от величины составляющей вектора напряженности, совпадающей по направлению с элементом контура l.

Согласно закону электромагнитной индукции ЭДС индукции определяется так:

. (5)

В соответствии с законом Ома для замкнутой цепи сила тока, проходящего через гальванометр, равна

, (6)

где R – сопротивление малой катушки;

r – внутреннее сопротивление гальванометра.

Отсюда

, (7)

где - величина заряда, прошедшего через гальванометр за время .

Подставим ЭДС из (7) в формулу (5). Тогда

,

или, так как , то

. (8)

Величина отклонения светового пятна гальванометра пропорциональна заряду:

  q. (9)

Используя соотношения (8) и (9), можно записать

,

где К – коэффициент пропорциональности.