
Задания С5
.doc
Задания С5
Уметь решать задачи на вычисления геометрических величин ( задачи по планиметрии ).
1.Дан ромб АВСЕ с острым углом В. Площадь ромба равна 320, а синус угла В равен 0,8. Высота СН пересекает диагональ ВЕ в точке К. Найдите длину отрезка СК.
2. Трапеция ABCD вписана в окружность. Найдите среднюю линию трапеции, если её большее основание AD равно 15, синус угла ВАС равен 1/3, синус угла ABD равен 5/9.
3. Радиус круга, описанного около равнобедренного треугольника, равен 8, а один из углов треугольника 120°. Найдите площадь треугольника.
4. Около равнобедренного треугольника АВС с основанием АС и углом при основании 75° описана окружность с центром О. Найдите её радиус, если площадь треугольника ВОС равна 16.
5. Диагонали трапеции СЕКМ ( ЕК и СМ – основания ) пересекаются в точке О. Площадь треугольника СОЕ равна 16, СО = 2ОК. Найдите площадь трапеции.
6. Найдите площадь равнобедренной трапеции, если основания равны 17 и 15, а диагональ перпендикулярна боковой стороне.
7. Меньшее основание равнобедренной трапеции равно 6, большее – 12., угол при основании равен 60°. Найдите радиус описанной окружности.
8.
В треугольнике АВС проведена медиана
АМ. Найдите площадь треугольника АВС,
если АС =
![]() .
АВ =10, угол МСА равен 45°.
.
АВ =10, угол МСА равен 45°.
9.
Найти площадь КМР, если КР = 5, медиана
РО =
![]() ,
,
![]() .
.
10.
В равнобедренную трапецию один из углов
которого равен 60°, а площадь равна
![]() ,
вписана окружность. Найти радиус этой
окружности.
,
вписана окружность. Найти радиус этой
окружности.
11.В
прямоугольной трапеции острый угол
30°., меньшее основание равно 5, а высота
![]() .
Найти площадь трапеции.
.
Найти площадь трапеции.
12. Основания трапеции равны 10 и 31, а боковые стороны равны 20 и 13. Найти высоту трапеции.
13.
В трапеции основания равны 24 и 8, а
диагонали равны 13 и
![]() .
Найдите площадь трапеции.
.
Найдите площадь трапеции.
14. Стороны треугольника равны 12, 16 и 20. Найдите высоту треугольника, проведенную из вершины большего угла.
15. Периметр прямоугольного треугольника равен 72, а радиус вписанной в него окружности равен 6. Найти диаметр описанной окружности.
16. Один катет прямоугольного треугольника равен 15, а проекция второго на гипотенузу равна 16. Найти диаметр окружности описанной вокруг треугольника.
17. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна 10. Найти площадь треугольника.
18. В равнобедренный треугольник АВС с основанием ВС вписана окружность, которая касается стороны АВ в точке М. Найти радиус окружности, если АМ = 6, ВМ = 24.
19.
Дан прямоугольный треугольник АВС с
прямым углом С. Через центр О вписанной
окружности проведен луч ВО, пересекающий
катет АС в точке М. Известно, что АМ=![]() ,
,![]() .
Найти гипотенузу треугольника.
.
Найти гипотенузу треугольника.
20. Основание равнобедренного треугольника равно 36. Вписанная окружность касается боковых сторон в точках М и Р, причем МР = 12. Найти периметр треугольника.
В треугольнике
АВС
![]() .
Около треугольника описана окружность
радиуса 12. Хорда ВК проходит через
середину М стороны АС, причем МК = 2.
Найдите ВМ.
.
Около треугольника описана окружность
радиуса 12. Хорда ВК проходит через
середину М стороны АС, причем МК = 2.
Найдите ВМ.
21. Найдите радиус окружности, вписанной в треугольник АВС, если она касается стороны АВ в точке Р и известно, что АС = АВ = 15, ВР = 12.
22. Остроугольный равнобедренный треугольник ВСК с основанием СК, равным 16, вписан в окружность с центром О и радиусом 10. Найдите площадь треугольника ВОС.
23. К окружности проведены касательные МА и МВ. Найти хорду АВ, если радиус окружности равен 20, а расстояние от М до АВ равно 9.
24. Окружность с центром О, вписанная в равнобедренный треугольник АВС с основанием АС, касается ВС в точке К, причем СК:ВК = 5:8. Найти площадь треугольника АВС, если его периметр равен 72.
25. В прямоугольном треугольнике биссектриса острого угла делит противолежащий катет на отрезки длиной 4 и 5. Определите площадь треугольника.
26. Стороны треугольника равны 13,14 и 15. Найдите отношение площадей описанного и вписанного в этот треугольник кругов.
27. Найти площадь треугольника, вписанного в круг радиуса 2, если два угла треугольника равны 60° и 45°.
28. Найти радиус окружности вписанной в ромб, диагонали которого равны 10 и 24.
29.Найти площадь ромба, если его высота 8, а острый угол 30°.
30. Найти площадь ромба, если его периметр равен 40, а диагонали относятся как 3:4.
31.
Острый угол ромба равен 60°, а его площадь
![]() .
Найти периметр ромба.
.
Найти периметр ромба.
32.
Периметр правильного шестиугольника
равен
![]() .
Найти площадь шестиугольника.
.
Найти площадь шестиугольника.
33.
Найти площадь правильного треугольника,
если радиус вписанной окружности равен
![]() .
.
Задания С5
34. Дан ромб ABCD, диагонали которого равны 3 и 4 . Из вершины тупого угла В проведены две высоты BE и BF. вычислите площадь четырехугольника BFDE.
35. На стороне AD ромба АВСD взята точка М причем MD = 0,3AD, BM = MC =11. Найдите площадь треугольника ВСМ.
36. В равнобедренной трапеции ABCD AD =10, DC =2, AB = CD = 5. Биссектриса угла BAD пересекает ВС в точке К. Найти длину биссектрисы угла АВК в треугольнике АВК.
37. В трапеции MPQF длина оснований MF и PQ равны 24 и 4 соответственно. Высота трапеции равна 5. Точка N лежит на стороне MP, MN:NP = 3:1. Найти площадь треугольника NQF.
38.
Дан квадрат ABCD
со стороной
![]() .
Определите расстояние между серединой
отрезка АМ, где М – середина ВС, и точкой
N
на стороне CD,
делящей её в отношении 3:1, считая от
вершины С.
.
Определите расстояние между серединой
отрезка АМ, где М – середина ВС, и точкой
N
на стороне CD,
делящей её в отношении 3:1, считая от
вершины С.
39. Около треугольника АВС описана окружность. Медиана треугольника АМ продлена до пересечения с окружностью в точке К. Найдите сторону АС, если АМ = 18, МК = 8, ВК = 10.
40.
Дан ромб АВСЕ. Окружность, описанная
около треугольника АВЕ, пересекает
большую диагональ ромба АС а точке К.
Найдите СК, если АВ = 8![]() ,
ВЕ = 16.
,
ВЕ = 16.
41.
Точка К лежит на стороне АВ треугольника
АВО, ВК = 12, АК = 4,
![]()
![]() .
Найдите площадь треугольника ОВК.
.
Найдите площадь треугольника ОВК.
42. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
43. Найдите расстояние от точки пересечения медиан прямоугольного треугольника до катета, равного 12, если гипотенуза равна 15.
44. Высоты РА и СВ остроугольного треугольника РСТ пересекаются в точке Н, угол СНР равен 110°. Найдите градусную меру угла РСО, если точка О – центр окружности, описанной около треугольника РСТ.
45. Треугольник АВС вписан в окружность с центром О и радиусом 4. Найдите площадь треугольника ВОС, если угол В равен 40°, а угол С равен 35°.
46. В равнобедренный треугольник АВС с основанием ВС вписана окружность. Она касается стороны АВ в точке М. Найдите радиус окружности, если АМ = 6, ВМ = 24.
47. Найдите радиус окружности, вписанной в треугольник ВСЕ, если она касается стороны ВС в точке Р и известно, что ВЕ = ВС = 15, СР = 12.
48.
Дан прямоугольный треугольник АВС с
прямым углом С. Через центр О вписанной
окружности проведен луч ВО, пересекающий
катет АС в точке М. Известно, что АМ = 8![]() ,
,
![]() .
Найдите гипотенузу.
.
Найдите гипотенузу.
49.
Найдите площадь правильного
двенадцатиугольника, если его сторона
равна
![]() .
.
50. В правильном шестиугольнике
ABCDEF диагональ АС равна
![]() .
Найдите площадь шестиугольника.
.
Найдите площадь шестиугольника.
51.Точка D и Е – основания высот непрямоугольного треугольника АВС, проведенных из вершин А и С соответственно.
Известно, что DE:AC = k, BC =a и АВ = b. Найдите сторону АС.
52. Окружности радиусов 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей,
Если АВ = 16.
53. Дана окружность и точка М. Точки А и В лежат на окружности, причем А – ближайшая к М точка окружности, а
В – наиболее удаленная от М точка окружности. Найдите радиус окружности, если МА = а и МВ = в.
54. В параллелограмме АВСD известны стороны АВ = а, ВС = в и угол ВАD равный α. Найдите расстояние между центрами
Окружностей, описанных около треугольников BCD и DAB.
55. Дан прямоугольный треугольник АВС с прямым углом при вершине В и углом α при вершине А. Точка D – середина
гипотенузы.
Точка С![]() симметрична точке С относительно прямой
ВD.
Найдите угол АС
симметрична точке С относительно прямой
ВD.
Найдите угол АС![]() В.
В.
56. Медиана ВМ треугольника АВС равна его высоте АН. Найдите угол МВС.
57. Высоты треугольника АВС пересекаются в точке Н. Известно, что отрезок СН равен радиусу окружности, описан-
Ной около треугольника. Найдите угол АСВ.
58. В треугольнике АВС проведены высоты ВМ и СN, О – центр окружности, касающейся стороны ВС и продолжении
Сторон АВ и АС. Известно, что ВС = 12, МN = 6. Найдите радиус окружности, описанной около треугольника ВОС.
59. Дана трапеция АВСD с боковыми сторонами АВ = 36 и СD =34, верхнее основание ВС = 10. Известно, что
Cos![]() Найдите ВD.
Найдите ВD.
60. На боковых сторонах АВ и СD трапеции с основаниями АD и ВС отмечены точки Р и Q соответственно, причем
PQ||AD. Прямая PQ разбивает трапецию на две трапеции, площади которых относятся как 1:2. Найдите PQ, если
AD = a, BC = b.
61. На стороне ВА угла АВС, равного 30°, взята точка D, что AD = 2 и ВD = 1. Найдите радиус окружности, прохо-
дящей через точки A, D и касающейся прямой ВС.
62. В треугольнике АВС на стороне ВС выбрана точка D так, BD:DC = 1:2. Медиана СЕ пересекает отрезок AD
в точке F. Какую часть площади треугольника АВС составляет площадь треугольника AEF.
63.
Дан параллелограмм АВСD,
AB
= 3, DC
= 5,
![]() A
= 60°. Окружность с центром в точке О
касается биссектрисы
A
= 60°. Окружность с центром в точке О
касается биссектрисы
Угла D и двух сторон параллелограмма, исходящих из вершины одного его острого угла. Найдите площадь
Четырехугольника АВОD.
Задания С5
64. Через середину стороны АВ квадрата АВСD проведена прямая, пересекающая прямые СD и AD в точках М и Т
соответственно и образующая с прямой АВ угол, тангенс которого равен 3. Найдите площадь треугольника ВМТ,
Найдите площадь треугольника ВМТ, если сторона квадрата АВСD равна 4.
65. Дана трапеция АВСD, основания которой ВС = 44, АD=100, АВ = СD = 35. Окружность, касающаяся прямых АD и АС касается стороны СD в точке К. Найдите длину отрезка СК.
_____________________________________________________________________________
Ответы:
1) 10. 2)
12. 3)
![]() .
4) 8. 5) . 6) 64. 7) 6. 8) 21. 9) 3. 10) 3. 11)
.
4) 8. 5) . 6) 64. 7) 6. 8) 21. 9) 3. 10) 3. 11)
![]() .
.
-
12. 13) 80. 14) 9,6. 15) 30. 16) 25. 17) 30. 18) 8. 19) 24. 20) 90. 21) 4.
-
40. 23) 24. 24) 240. 25) 54. 26)
 27)
27)
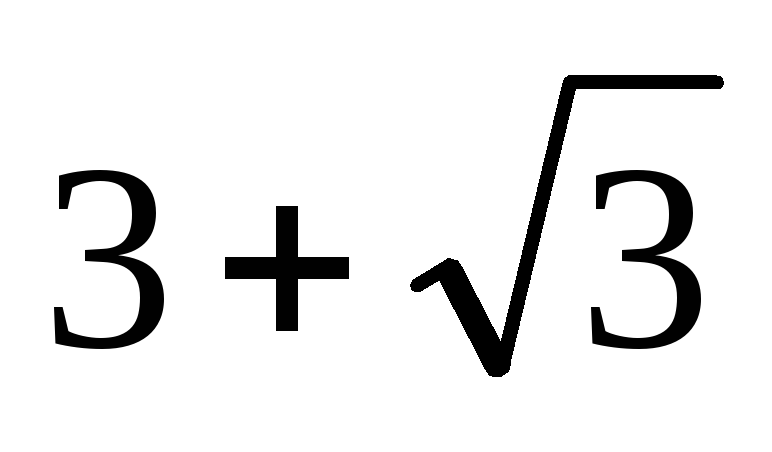 .
28)
.
28)
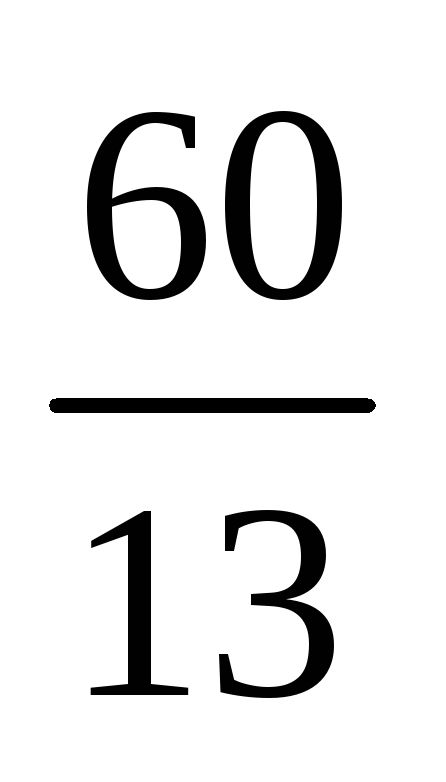 .
29) 128.
.
29) 128.
30) 96. 31) 24. 32)
![]() .
33)
.
33)
![]() .
34) 4,32. 35)
.
34) 4,32. 35)
![]() .
36)
.
36)
![]() .
37) 22,5.
.
37) 22,5.
38) 25. 39) 15. 40) 12. 41) 48. 42) 80. 43) 3. 44) 20. 45) 4.
46) 90. 47) 4. 48) 24.
49) 108. 50) 24. 51)
![]() 52)21 и 9.
52)21 и 9.
53)
![]() .
54)
.
54)
![]() 55)
55)
![]()
56.) 30° или 150°. 57)
60° или 120°. 58)
![]() 59)
59)
![]()
60)
![]() .
64) 2 или 10. 65) 5 или 30.
.
64) 2 или 10. 65) 5 или 30.
