
- •Лабораторная работа № 1
- •Варианты заданий
- •Лабораторная работа № 2
- •Лабораторная работа № 3
- •Лабораторная работа № 6 Интерполирование функций
- •Лабораторная работа № 7 Интерполирование функций двух переменных
- •Лабораторная работа № 8 Метод золотого сечения
- •Лабораторная работа № 9 Метод Куммера
- •Варианты заданий
- •Лабораторная работа № 10 Решение систем нелинейных уравнений методом Ньютона Пусть задана система двух нелинейных уравнений с двумя неизвестными
- •Лабораторная работа № 11 Решение систем нелинейных уравнений методом итерации
- •Лабораторная работа № 12 Решение систем линейных уравнений методом Гаусса
- •Лабораторная работа № 13 Метод прогонки
- •Варианты заданий
- •Варианты заданий
- •Лабораторная работа № 20 Метод Милна
- •Лабораторная работа № 21 Метод Адамса
- •Лабораторная работа № 23 Решение систем дифференциальных уравнений методом Рунге—Кутта
- •Лабораторная работа № 24 Задача линейного программирования
- •Лабораторная работа № 25 Транспортная задача
- •Лабораторная работа № 26 Метод наискорейшего спуска
- •Лабораторная работа № 27 Метод дробления шага
- •Лабораторная работа № 28 Метод покоординатного спуска
- •Лабораторная работа № 29 Метод случайного поиска
- •Лабораторная работа № 30 Эмпирические формулы. Линейная зависимость
- •Лабораторная работа № 31 Решение краевой задачи методом сеток
- •Лабораторная работа № 35 Динамическое программирование
- •Корни нелинейных уравнений
- •Интерполирование функций
- •Двумерная интерполяция
- •Метод золотого сечения (лабораторная работа № 8)
- •Решение систем нелинейных уравнений (лабораторные работы №10— 11)
- •Решение систем линейных уравнений
- •Решение систем линейных уравнений методом прогонки
- •Приближенные значения интегралов
- •Приближенные решения системы дифференциальных уравнений
- •Задача линейного программирования
- •Максимальная прибыль
- •Транспортная задача
- •Значения функции в точке минимума
- •Динамическое программирование
- •Список литературы
Лабораторная работа № 28 Метод покоординатного спуска
Метод
применяется для отыскания минимума
функции n
переменных. Находится некоторое
начальное приближение
![]() (0)
точки минимума функции. Затем выбирается
направление спуска параллельно
оси 0х1
и решается задача одномерной минимизации
функции. Величина 0
определяется из условия
(0)
точки минимума функции. Затем выбирается
направление спуска параллельно
оси 0х1
и решается задача одномерной минимизации
функции. Величина 0
определяется из условия
 .
.
Определяется
первое приближение точки минимума
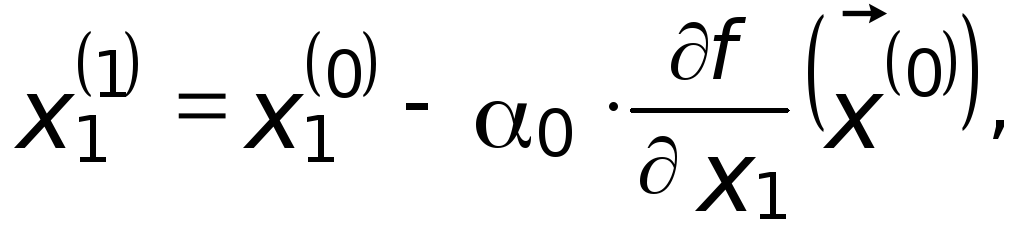 а все остальные координаты остаются
без изменения. При следующем уточнении
точки минимума спуск производится вдоль
линии, параллельной оси 0х2.
Величина 1
определяется из условия
а все остальные координаты остаются
без изменения. При следующем уточнении
точки минимума спуск производится вдоль
линии, параллельной оси 0х2.
Величина 1
определяется из условия
 .
.
Затем
определяется второе приближение точки
минимума
 а все остальные координаты остаются
без изменения. Аналогичным способом
спуск продолжается в направлении
следующих координат. После этого спуск
снова начинается в направлении
первой, второй и т. д.
координаты. Процесс заканчивается
при выполнении условия
а все остальные координаты остаются
без изменения. Аналогичным способом
спуск продолжается в направлении
следующих координат. После этого спуск
снова начинается в направлении
первой, второй и т. д.
координаты. Процесс заканчивается
при выполнении условия
grad
f(![]() (k+1))
<
.
(k+1))
<
.
Пример. Найти минимум функции
f (x1,x2) = 2x1 - 3x2 + exp (x12 + x24).
Решение. Задачу решим
методом покоординатного спуска. Возьмем
= 0,001.
В качестве начального выберем вектор
![]() =
(0;0).
Тогда
=
(0;0).
Тогда




grad
f
=
 +
+ grad
grad
![]()
![]()
grad
![]()
3,60555.
3,60555.
Составим
функцию
 которую нужно минимизировать по параметру
.
Для минимизации этой функции применим
метод дробления шага. Результаты
вычислений занесены в табл. 6.
которую нужно минимизировать по параметру
.
Для минимизации этой функции применим
метод дробления шага. Результаты
вычислений занесены в табл. 6.
Можно
считать, что минимум функции достигается
в точке
![]() =(-
0,547; 0,743) и равен -1,493638.
=(-
0,547; 0,743) и равен -1,493638.
Таблица 6
|
k |
|
|
|
|
|
|
0 |
(0; 0) |
1 |
2 |
-3 |
3,605551 |
|
1 |
(-0,652918; 0,00000) |
0,225747 |
0,000005 |
-3 |
3,000000 |
|
2 |
(-0,652918; 0,720492) |
-1,462048 |
-0,618545 |
-0,000015 |
0,618545 |
|
3 |
(-0,558881; 0,720492) |
-1,489943 |
-0,000007 |
-0,323116 |
0,323116 |
|
4 |
(-0,558881; 0,740601) |
-1,493255 |
-0,063737 |
-0,000017 |
0,063737 |
|
5 |
(-0,548115; 0,740601) |
-1,493597 |
-0,000004 |
-0,035558 |
0,035558 |
|
6 |
(-0,548115; 0,742701) |
-1,493634 |
-0,006869 |
-0,000011 |
0,006869 |
|
7 |
(-0,546942; 0,742701) |
-1,493638 |
0,000002 |
-0,003863 |
0,003863 |
|
8 |
(-0,546942; 0,742927) |
-1,493638 |
0,000742 |
-0,000023 |
0,000742 |
Задание.
Методом покоординатного спуска найти
минимум функции
![]() где k
— номер фамилии студента в журнале
преподавателя. Значения х1
и х2,
в которых функция достигает минимума,
определить с точностью
= 0,0001.
Начальное приближение найти методом
случайного поиска.
где k
— номер фамилии студента в журнале
преподавателя. Значения х1
и х2,
в которых функция достигает минимума,
определить с точностью
= 0,0001.
Начальное приближение найти методом
случайного поиска.
Лабораторная работа № 29 Метод случайного поиска
Метод
применяется для нахождения минимума
некоторой функции
![]() ,
заданной в некоторой области. Для этого
разыгрывается равномерно распределенный
в этой области случайный вектор
,
заданной в некоторой области. Для этого
разыгрывается равномерно распределенный
в этой области случайный вектор
![]() .
Определяется
значение функции в этой точке.
Запоминается значение вектора и значение
функции. Затем разыгрывается новое
значение случайного вектора и
определяется новое значение функции.
Если новое значение меньше запомненного,
то запоминается новое значение функции
и координаты нового вектора. В противном
случае никаких операций не
производится.
.
Определяется
значение функции в этой точке.
Запоминается значение вектора и значение
функции. Затем разыгрывается новое
значение случайного вектора и
определяется новое значение функции.
Если новое значение меньше запомненного,
то запоминается новое значение функции
и координаты нового вектора. В противном
случае никаких операций не
производится.
Затем выполняется следующий из N шагов решения задачи. Запомненные значения функции и координат вектора и являются приближенным решением задачи. Чем больше задано значение N, тем точнее будет получено решение задачи.
Пример. Найти минимум функции
![]()
Решение. При решении этой задачи в области [(-1;0);(0;1)] при N = 32000 были получены следующие результаты: x1 = -0,541633; x2 = 0,742442; F = -1,493550. При повторном решении задачи при этих же условиях были получены результаты, отличающиеся в третьем знаке после запятой от приведенных выше, так как при повторном решении разыгрываются другие значения вектора и результаты решения задачи несколько изменяются.
Задание. Методом случайного поиска найти минимум функции
![]() где
k
— номер фамилии студента в журнале
преподавателя. При вычислениях взять
N
= 10000. Запустить программу три раза.
Сравнить полученные результаты.
где
k
— номер фамилии студента в журнале
преподавателя. При вычислениях взять
N
= 10000. Запустить программу три раза.
Сравнить полученные результаты.


