Лабораторна робота №1

Тема: Побудова та аналіз одночинникової економетричної моделі

Мета: На запропонованій базі даних побудувати й оцінити одночинникову економетричну модель, а також провести аналіз її достовірності

Короткі теоретичні відомості

При дослідженні різноманітних економічних явищ і процесів у вигляді економетричної моделі зв’язків між економічними показниками, часто можна виявити такий показник, який здійснює найсуттєвіший вплив на результативну ознаку і є найбільш важливим.

Кількісний зв’язок між змінною у, що характеризує результативну ознаку і незалежною змінною , що характеризує найбільш важливий чинник, дає одночинникова (однофакторна) економетрична модель. Загальний вигляд такої моделі:

, (1.1)

де e – стохастична складова (залишки, відхилення) моделі.

Аналітична форма економетричної моделі залежить від економетричної сутності зв’язків.

В економічній практиці найбільш поширеними є такі форми аналітичних залежностей:

; лінійна (1.2)

; експоненціальна (1.3)

; степенева (1.4)

; обернена (1.5)

де , – невідомі параметри моделі.

За допомогою елементарних перетворень нелінійні форми залежності (1.3-1.5) можна привести до лінійних, не враховуючи стохастичні складові моделі.

Наприклад, логарифмуванням залежності (1.3) і (1.4) можна привести до вигляду:

, (1.6)

. (1.7)

Після чого, шляхом заміни змінних легко отримати явні лінійні аналітичні залежності.

Нехай лінійна одночинникова економетрична модель має вигляд:

, (1.8)

Стохастична складова е має нульове математичне сподівання і постійну дисперсію ().

В цьому випадку невідомі параметри моделі (1.8) можна оцінити на основі звичайного методу найменших квадратів (1 МНК).

З курсу математики відомо, що 1 МНК використовує принцип мінімізації квадратів залишків стохастичної складової моделі. Застосовуючи необхідну умову мінімізації функції двох змінних, отримуємо систему нормальних рівнянь:

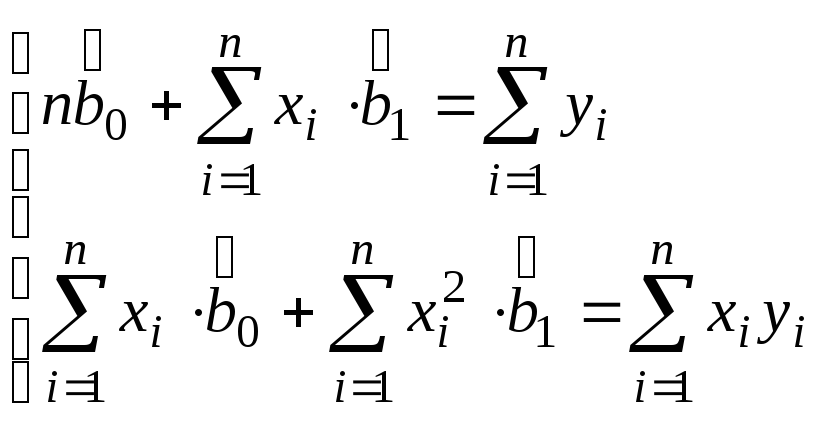, (1.9)

де , ,, – адитивні величини, які можна розрахувати на основі бази вихідних даних, n – кількість статистичних спостережень.

Розв’язок системи рівнянь (1.9) дає можливість одержати оцінки невідомих параметрів моделі (1.8) .

Обчислити параметри економетричної моделі можна також за виразами:

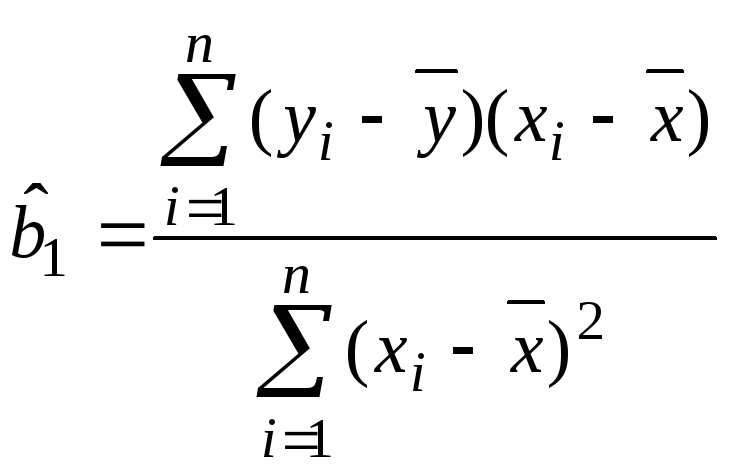, (1.10)

. (1.11)

Або:

; (1.12)

де – коваріація між змінними і ; – дисперсія чинника .

Лінійна економетрична модель матиме вигляд:

, (1.13)

де символ “кутик” над y, означає, що їхні значення отримують в результаті розрахунків, тобто вони є оцінками того реального значення, яке можна встановити в процесі статистичного спостереження.

Достовірність побудованої моделі (1.13) можна перевірити, знаючи дисперсії залишків () та результативної ознаки ():

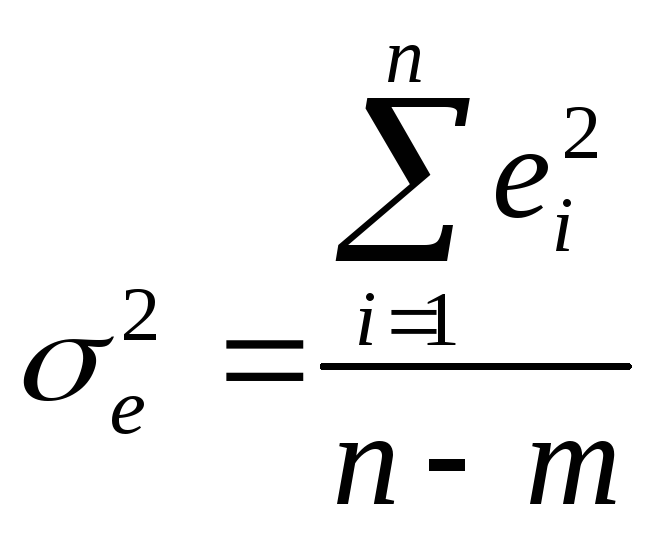, (1.14)

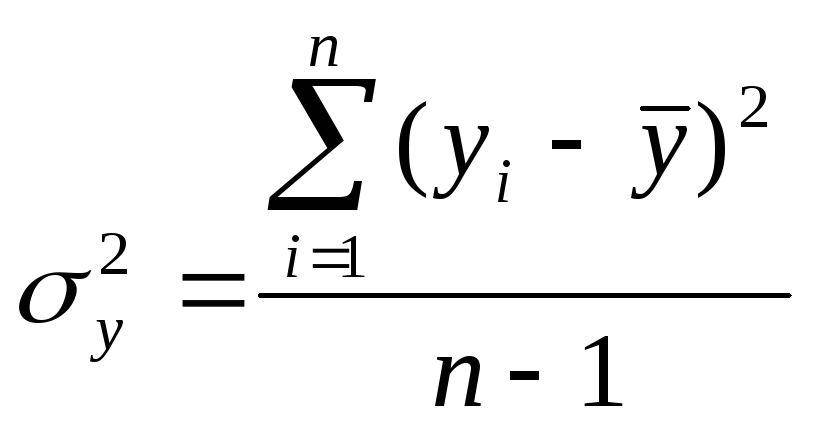, (1.15)

де – кількість невідомих параметрів моделі (у даному випадку ).

Коефіцієнти детермінації і кореляції визначають за виразами:

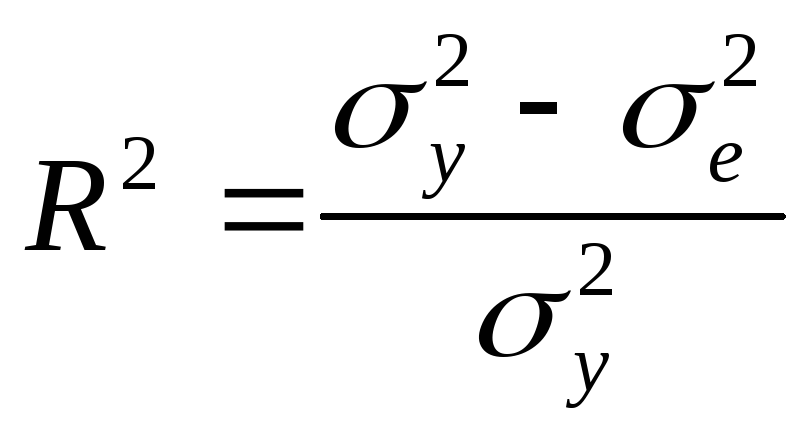; (1.16)

. (1.17)

Стандартну помилку кожного параметра моделі (1.13) знаходять за виразом:

, (1.18)

де – відповідний діагональний елемент матриці помилок С – матриці, оберненої до матриці системи нормальних рівнянь (1.10):

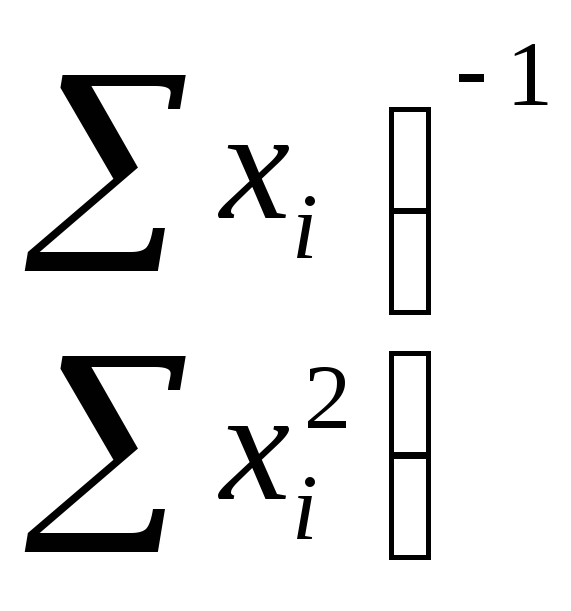= , (1.19)

Враховуючи (1.19) та (1.18), маємо вирази для стандартної та відносної оцінок параметрів моделі:

, (1.20)

, (1.21)

, (1.22)

, (1.23)

За оціненим параметром (відношення приросту функції до приросту аргументу) можна визначити коефіцієнт еластичності:

, (1.24)

який показує, на скільки відсотків у середньому зміниться результат, якщо чинник зміниться на один відсоток.