
- •1. Действия с обыкновенными и десятичными дробями.
- •Задачи:
- •2. Степень с натуральным показателем.
- •Задачи:
- •Домашнее задание:
- •3. Одночлены и многочлены. Степень одночлена и многочлена. Стандартный вид многочлена. Действия над многочленами. Преобразование целого выражения в многочлен.
- •Домашнее задание:
- •6. Линейная функция, ее свойства и график.
- •Задачи:
- •Домашнее задание:
- •7. Решение и исследование линейных уравнений.
- •Задачи:
- •Домашнее задание:
- •8. Понятие модуля числа. График функции .
- •Задачи:
- •Домашнее задание:
- •9. Аналитическое и графическое решение уравнений, содержащих переменную под знаком модуля.
- •Задачи:
- •Домашнее задание:
- •10. Системы линейных уравнений. Аналитическое и графическое решение систем, сводящихся к линейным.
- •Домашнее задание:
Домашнее задание:
Вил: стр. 46-51, Глава II, №73 (а, в); №78 (к); №81 (а, г); №101 (а, г, д, ж);
Гал: стр. 14, №2.7 (а); №2.9 (а); №2.4 (б); №2.5 (а); №2.6 (б); №2.10 (в);
Вил: стр. 57, Глава II, №124 (г, е, к);
Гал: стр. 14, №2.8 (б);
-
Разложить на множители:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
Вил: стр. 82-86, Глава II, №221 (в); №229 (а, г, д); №230 (в, е); №260 (а, в).
6. Линейная функция, ее свойства и график.
Функция вида
![]() называется линейной. Название это
связано с тем, что графиком линейной
функции является невертикальная прямая
линия (строится по двум точкам).
называется линейной. Название это
связано с тем, что графиком линейной
функции является невертикальная прямая
линия (строится по двум точкам).
Число k называется
угловым коэффициентом, поскольку
оно отвечает за угол наклона прямой к
оси абсцисс (чем меньше число k
по модулю, тем ближе прямая к горизонтальной;
чем больше
![]() ,
тем ближе прямая к вертикальной).
,
тем ближе прямая к вертикальной).
Если угловой коэффициент положителен, то график линейной функции «выходит» из третьей координатной четверти в первую (движение «в горку»); если же k<0, то из второй – в четвертую (движение «под горку»). При k=0 прямая горизонтальна.
По угловым коэффициентам двух прямых можно судить об их взаимном расположении: если у двух линейных функций одинаковые угловые коэффициенты, понятно, что их графики либо параллельны, либо совпадают. Графики двух линейных функций пересекаются тогда и только тогда, когда у них разные угловые коэффициенты.
Число b в уравнении
линейной функции называется свободным
членом. Поскольку при подстановке в
линейную функцию аргумента x=0
получается
![]() ,
то точка (0;b) лежит на
графике линейной функции. Другими
словами, график линейной функции
пересекает ось ординат в точке (0;b).
,
то точка (0;b) лежит на
графике линейной функции. Другими
словами, график линейной функции
пересекает ось ординат в точке (0;b).
Если свободный член равен нулю, то
линейная функция имеет вид
![]() ,
а ее график проходит через начало
координат. Функцию
,
а ее график проходит через начало
координат. Функцию
![]() называют функцией прямой
пропорциональности.
называют функцией прямой
пропорциональности.
Если у двух линейных функций угловые коэффициенты одинаковы, то их графики совпадают тогда и только тогда, когда совпадают их свободные члены (другими словами, когда прямые заданы одним и тем же уравнением).
Уравнение вертикальной прямой
записывается в виде
![]() ,
где a – некоторое
число.
,
где a – некоторое
число.
Задачи:
-
Постройте графики следующих функций и уравнений:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
-
Найдите координаты точки пересечения графиков уравнений, не выполняя построений:
а)
![]() и
и
![]() ; б)
; б)
![]() и
и
![]() ; в)
; в)
![]() и
и
![]() .
.
-
Подберите значение углового коэффициента k таким образом, чтобы прямая
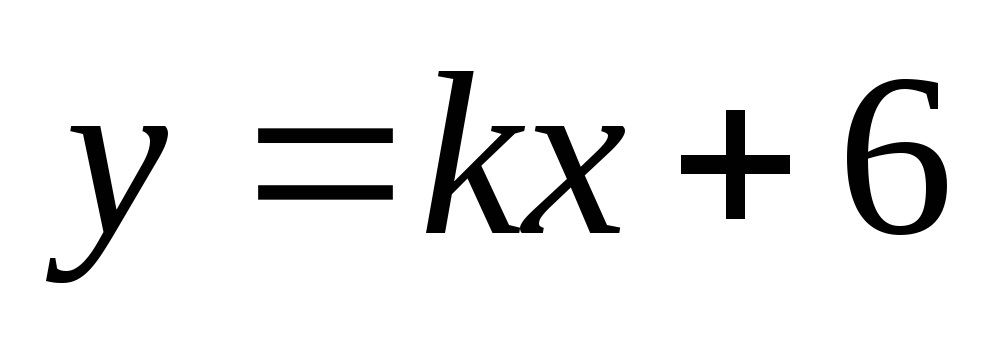 прошла через следующую точку:
прошла через следующую точку:
а) A(2;-1); б) B(5;6); в) C(0;6); г) D(0;8).
-
Определите значение b таким образом, чтобы прямая
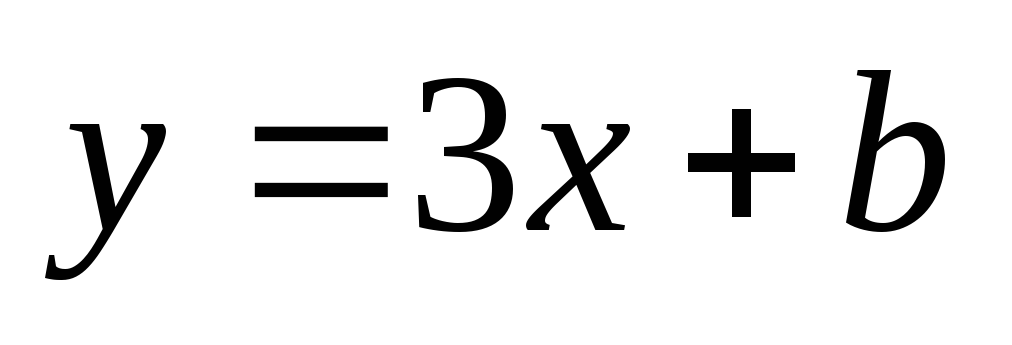 прошла через следующую точку:
прошла через следующую точку:
а) A(![]() ;
;
![]() ); б)
B(0;0); в) C(0;4).
); б)
B(0;0); в) C(0;4).
-
Запишите уравнение прямой, проходящей через точку A(-2;5) параллельно прямой, заданной уравнением
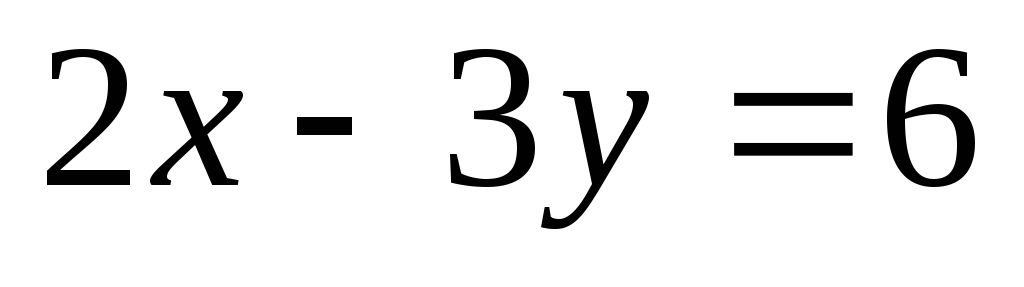 .
. -
При каких значениях k и b прямая
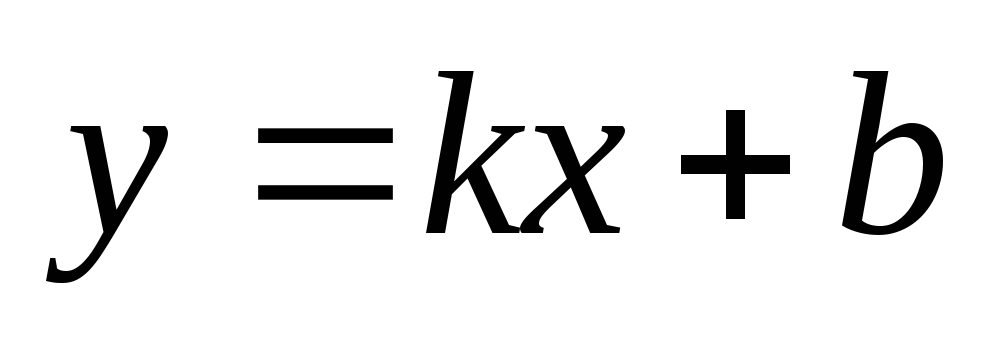 проходит через следующие точки:
проходит через следующие точки:
а) A(2;1) и B(-1;2); б) C(-1;3) и D(2004;3); в) E(-3;2) и F(‑3;1,5)?
-
(Лицей-8, 1999 г.) График линейной функции проходит через точки A(1;2) и B(-3;-4). Задайте формулой эту функцию и постройте ее график. Определите, при каких значениях x значение y: а) равно нулю; б) больше нуля; в) меньше нуля.
-
(Лицей-8, 2002 г.) Ордината точки A в три раза больше абсциссы. Найдите координаты точки A, если известно, что точка A принадлежит прямой
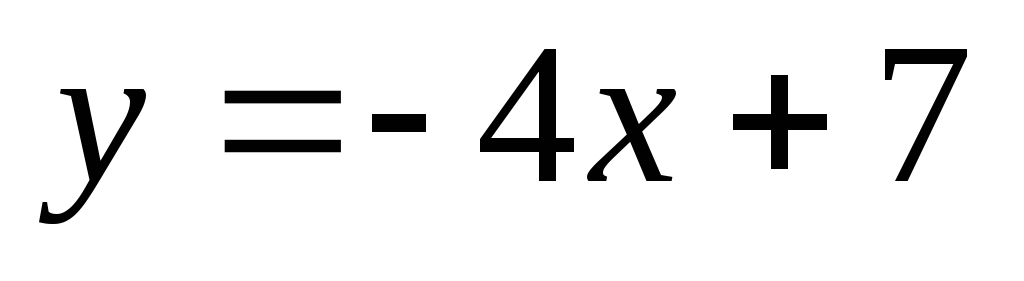 .
Изобразите прямую и точку A
на координатной плоскости. При каких
значениях аргумента x
функция y больше
нуля?
.
Изобразите прямую и точку A
на координатной плоскости. При каких
значениях аргумента x
функция y больше
нуля? -
(Лицей-8, 2001 г.) При каких значениях b три прямые пересекаются в одной точке:
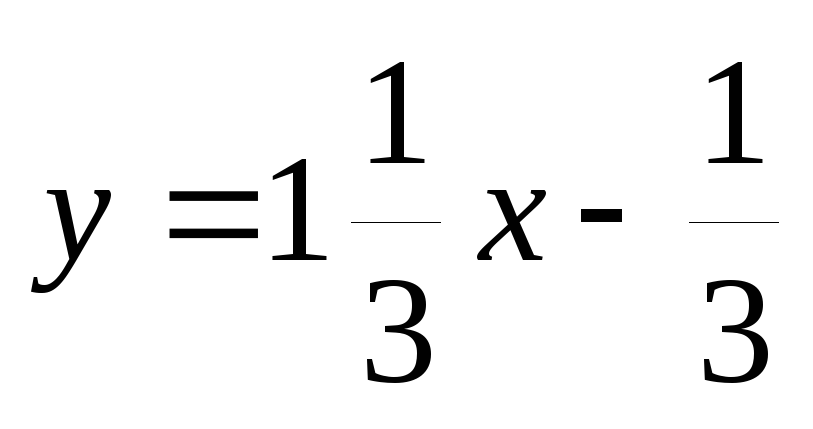 ;
;
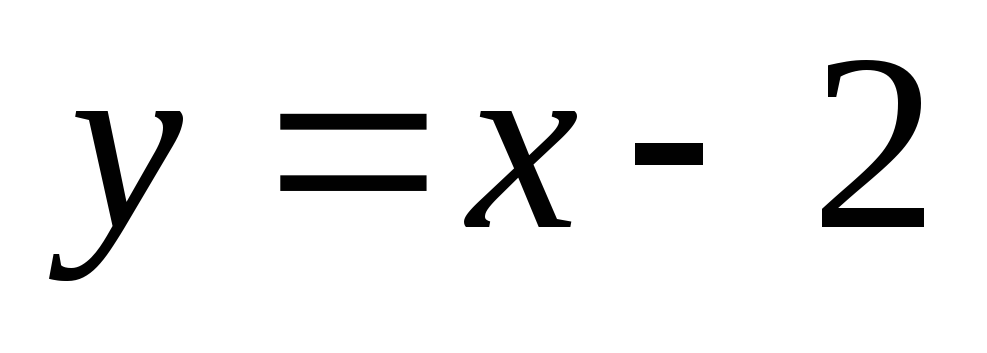 ;
;
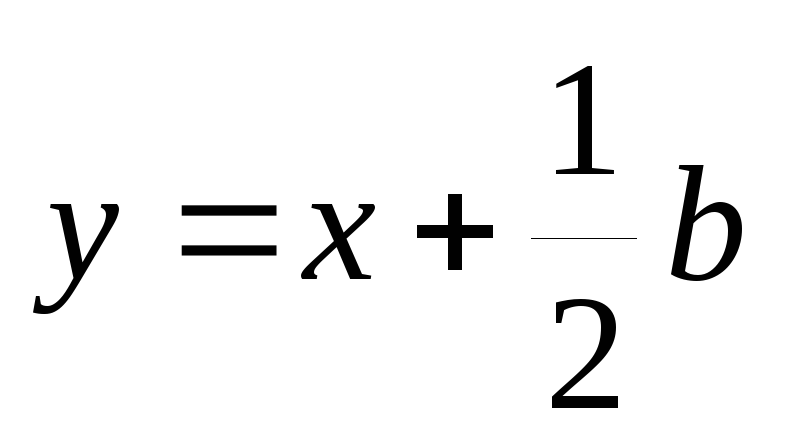 ?
? -
(Лицей-8, 2003 г.) Найдите значение b, при котором графики функций
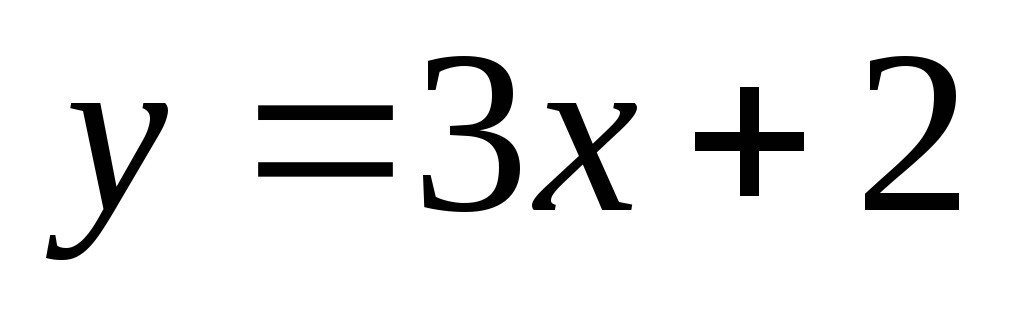 и
и
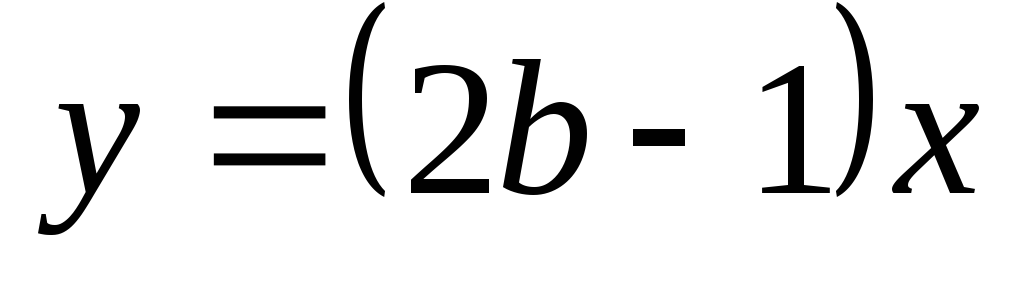 пересекаются в точке с ординатой -4.
Постройте эти графики и найдите
координаты точки их пересечения.
Постройте точку, симметричную точке
пересечения графиков относительно
оси абсцисс и запишите ее координаты.
пересекаются в точке с ординатой -4.
Постройте эти графики и найдите
координаты точки их пересечения.
Постройте точку, симметричную точке
пересечения графиков относительно
оси абсцисс и запишите ее координаты. -
(Лицей-8, 1995 г.) При каком b прямые
 и
и
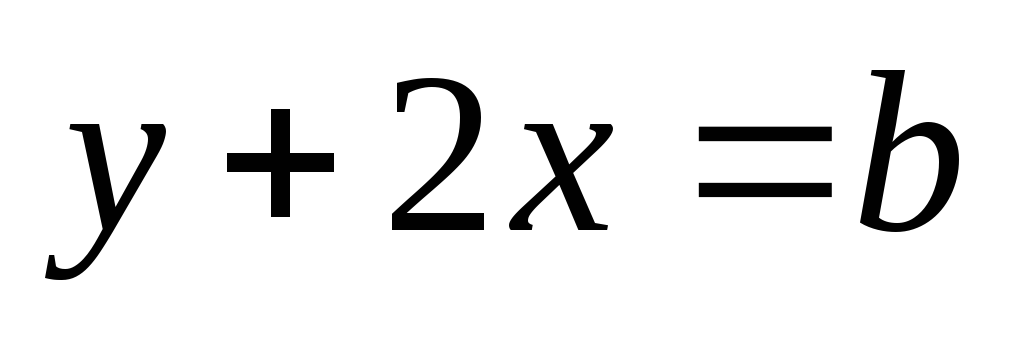 пересекаются в точке, принадлежащей
прямой
пересекаются в точке, принадлежащей
прямой
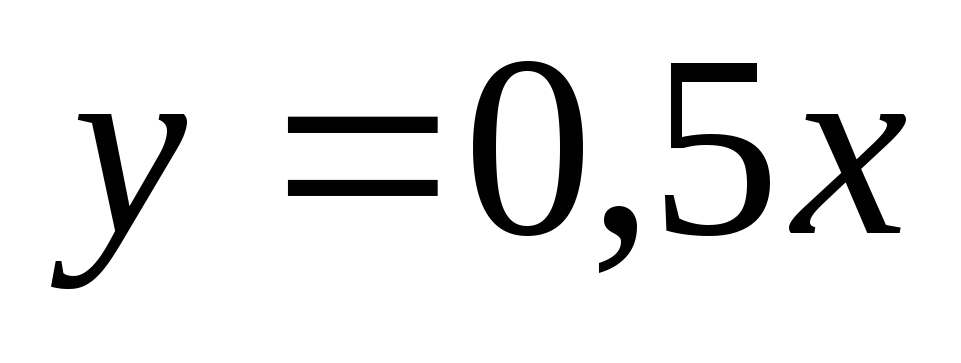 ?
? -
(Лицей-8, 1997 г.) Прямые
 и
и
 пересекаются в точке M(x0;y0).
Положение этой точки на прямой
пересекаются в точке M(x0;y0).
Положение этой точки на прямой
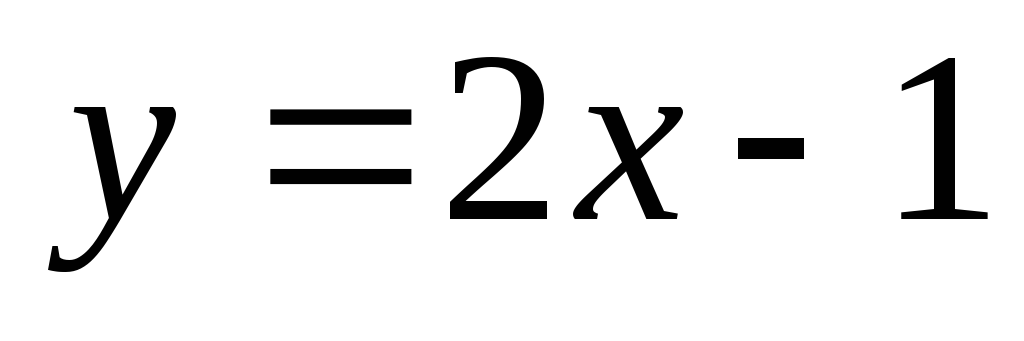 зависит от значения a.
1) Найдите абсциссу x0
точки M(x0;y0)
при a=1. 2) Какое число
следует подставить вместо a,
чтобы точка пересечения имела абсциссу
x0=1?
зависит от значения a.
1) Найдите абсциссу x0
точки M(x0;y0)
при a=1. 2) Какое число
следует подставить вместо a,
чтобы точка пересечения имела абсциссу
x0=1?-
(LXVII Московская математическая олимпиада, окружной тур, 9 класс, 1.02.2004; №2) Если первый автомобиль сделает 4 рейса, а второй – 3 рейса, то 21 тонну груза они вместе перевезти не смогут. Если же первый сделает 7 рейсов, а второй – 4 рейса, то они смогут перевезти более 33 тонн груза. Какой из автомобилей имеет большую грузоподъемность?
-
