1. Действия с обыкновенными и десятичными дробями.
Основное свойство дроби заключается
в том, что числитель и знаменатель дроби
можно умножить (или разделить) на одно
и то же число, не равное нулю; дробь при
этом не изменится:
,
где
.
На основном свойстве дроби базируется
сокращение дробей (деление числителя
и знаменателя на одно и то же число) и
приведение дробей к общему знаменателю
путем домножения числителя и знаменателя
на дополнительный множитель.
Д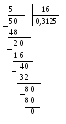
ействия
с десятичными дробями выполняются
аналогично действиям с целыми числами.
Чтобы преобразовать обыкновенную дробь
в десятичную (если это возможно), нужно
выполнить деление числителя дроби на
знаменатель «уголком». К примеру, 
.
Для преобразования десятичной дроби
необходимо просто записать ее в виде
обыкновенной и, если возможно, выполнить
сокращения:
.
Для выполнения сложения или вычитания
обыкновенных дробей их сначала
приводят к общему знаменателю, а затем
выполняют соответствующее действие с
числителями, оставляя общий знаменатель
без изменений. То есть
.
Ч
тобы
преобразовать дробь с целой частью в
неправильную дробь надо прибавить к
ее целой части дробную. К примеру,
.
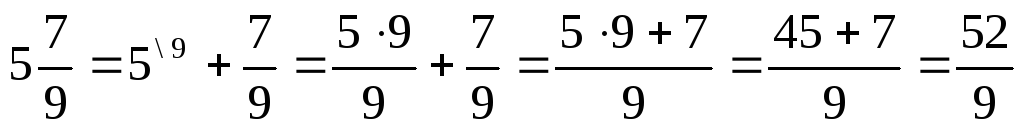Напротив, чтобы выделить целую часть
неправильной дроби необходимо
выполнить деление ее числителя на
знаменатель «уголком»:
.
При умножении двух дробей перемножаются
их числители и знаменатели:
.
Чтобы поделить число на дробь, надо
умножить это число на обратную ей дробь:
,
где c≠0.
Задачи:
-
Вычислить:
а)
;
б)
;
в)
.
-
Решить уравнение:
.
2. Степень с натуральным показателем.
Степенью числа a
с натуральным показателем n
(n>1) называется
произведение n
множителей, каждый из которых равен a:
;
степенью числа a с
показателем 1 называется само число a:
.
Свойства степеней с натуральным показателем:
-
Умножение степеней с одинаковыми основаниями:
. -
Деление степеней с одинаковыми основаниями:
,
где a≠0, и m>n. -
Возведение степени в степень:
. -
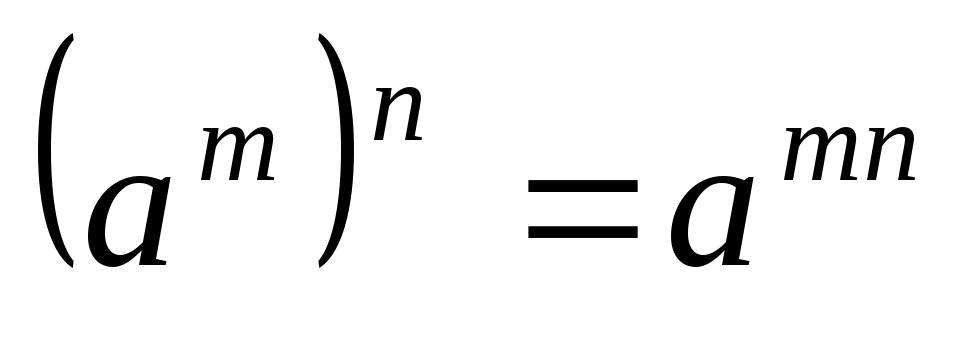Возведение произведения в степень:
. -
Возведение частного в степень:
,
где b≠0.
Задачи:
-
Записать выражение в виде произведения степеней. Указать основания и показатели степеней:
а)
;
б)
;
в)
.
-
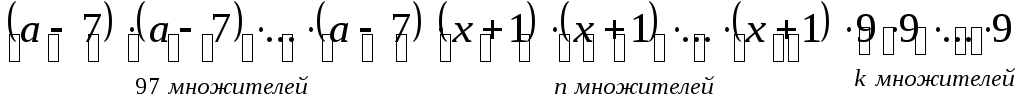Зная, что
,
найти:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
.
-
Вычислить:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
(n – натуральное
число, большее 1);
к)
(n – натуральное
число);
л)
(n – натуральное
число, большее 2).
-
Упростить выражение:
а)
;
б)
;
в)
.
-
Упростить выражение и вычислить его значение при
,
,
:
.
Домашнее задание:
-
Вычислить:
а)
;
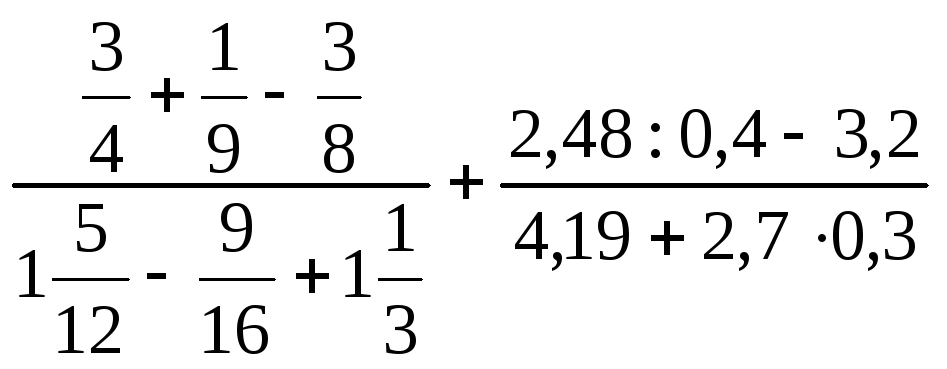б)
;
в)
.
-
Решить уравнение:
. -
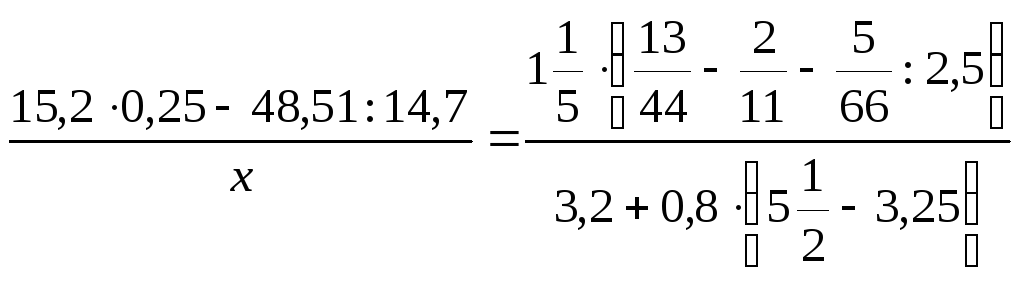Вычислить:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
(n – натуральное
число, большее 1);
з)
(n – натуральное
число);
и)
(n – натуральное
число, большее 2).
-
Упростить выражение:
а)
;
б)
;
в)
;
г)
.
-
Упростить выражение и вычислить его значение при
,
,
:
.
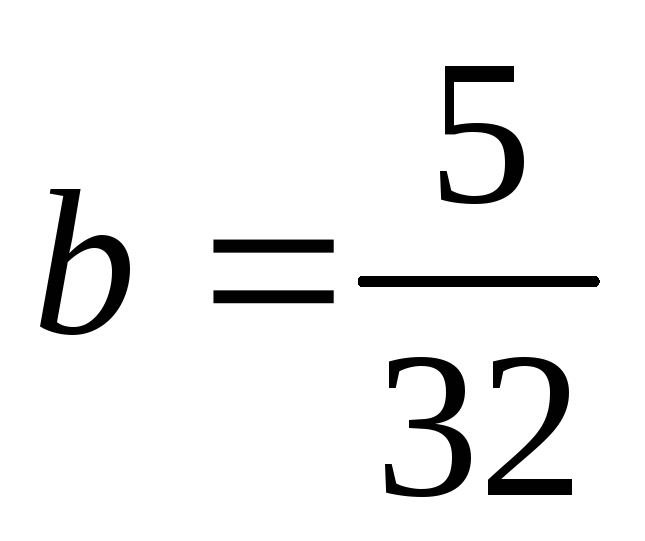