Тема 2. Определеный интеграл и его приложения

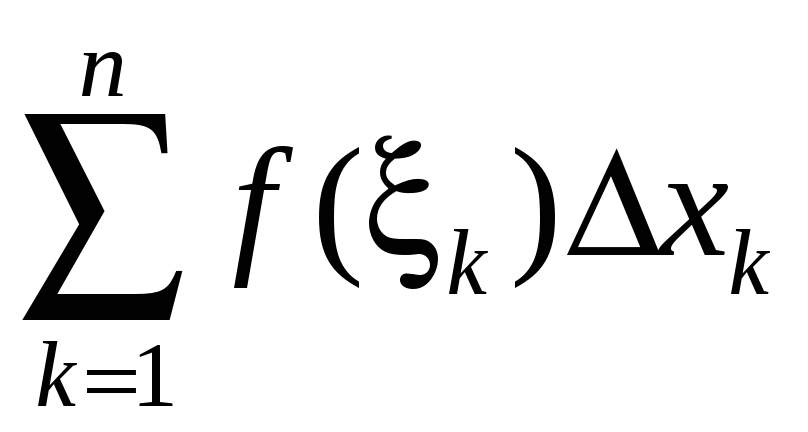Интегральной суммой функции на отрезке называется сумма , где , причем .

Если существует предел интегральной суммы при , не зависящий от способа разбиения отрезка на частичные отрезки и выбора промежуточных точек , то функция называется интегрируемой на этом отрезке, а сам предел – определенным интегралом от функции на отрезке и обозначается .

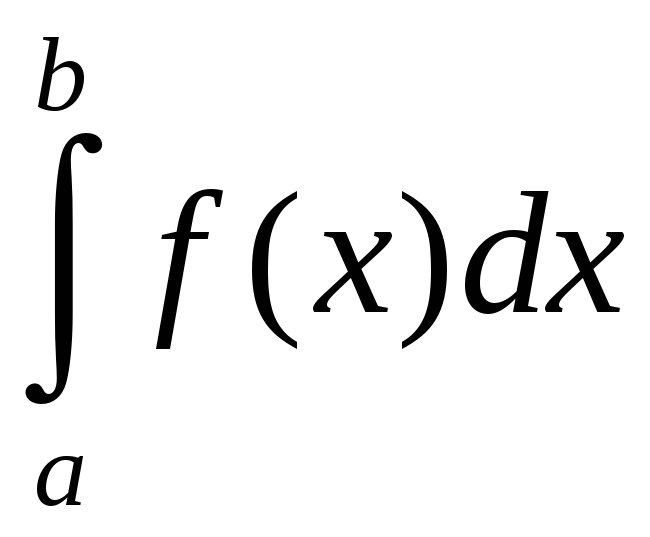Таким образом,

.

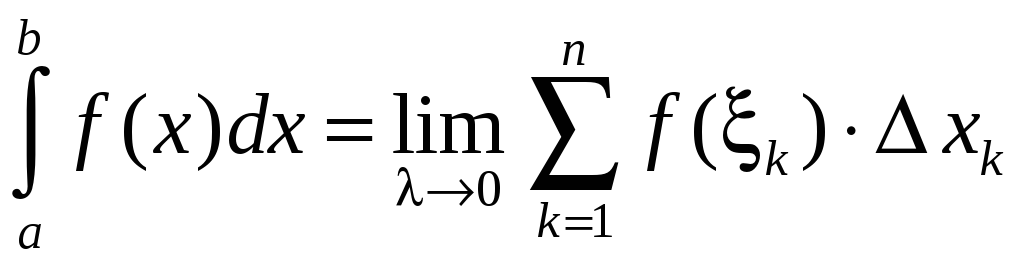Если кусочно-непрерывна на , то она интегрируема на этом отрезке.

Пусть – одна из первообразных непрерывной на функции , тогда справедлива формула Ньютона–Лейбница

. (2.1)

Для любых .

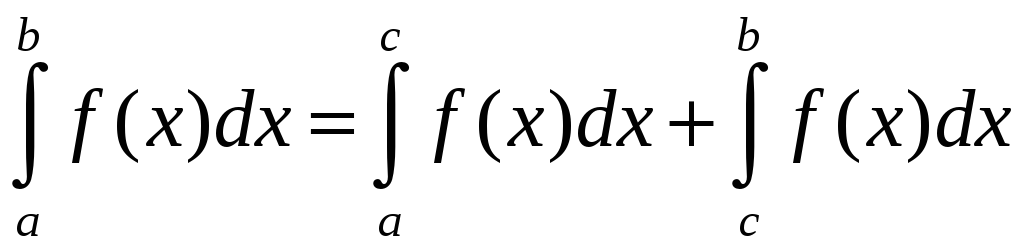Если функции и непрерывны вместе со своими производными на , то имеет место формула интегрирования по частям:

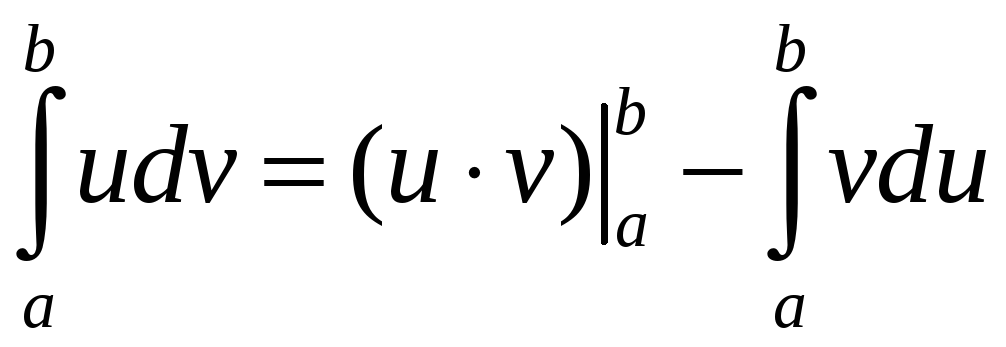. (2.2)

Если функция непрерывна на , а функция непрерывно дифференцируема и строго возрастает на , то справедлива формула

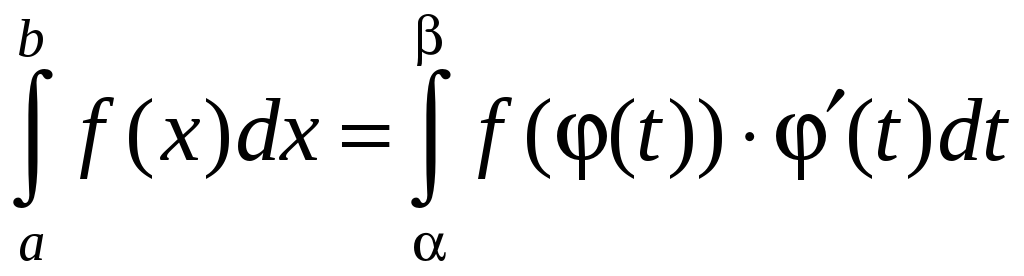, (2.3)

называемая формулой замены переменной в определенном интеграле.

Пример 2.1. Вычислить интегралы:

а) 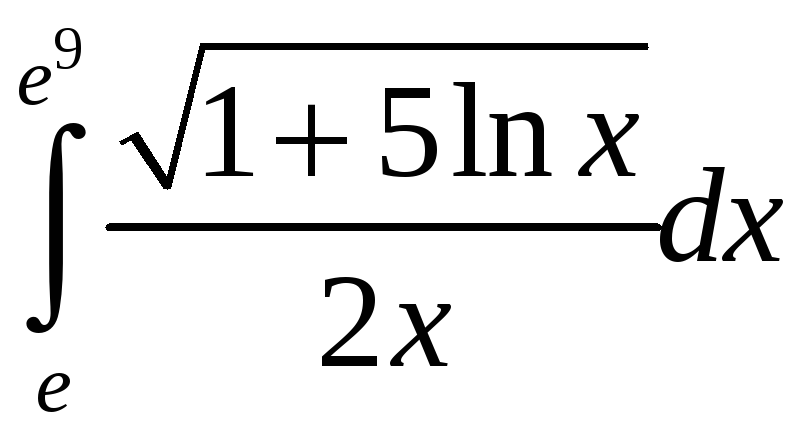; б) .

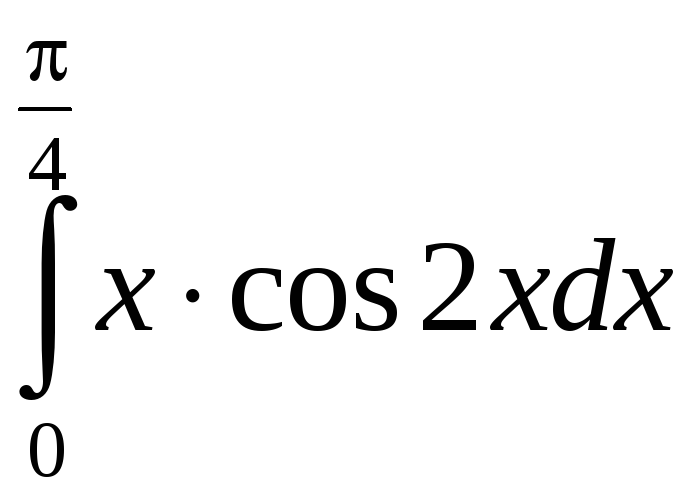Решение.

а) Введем новую переменную интегрирования . Тогда . Найдем пределы интегрирования по переменной . Из формулы при , следует, что , т. е. ; при , следует, что , т.е. . Тогда по формуле (2.3) получаем

=.

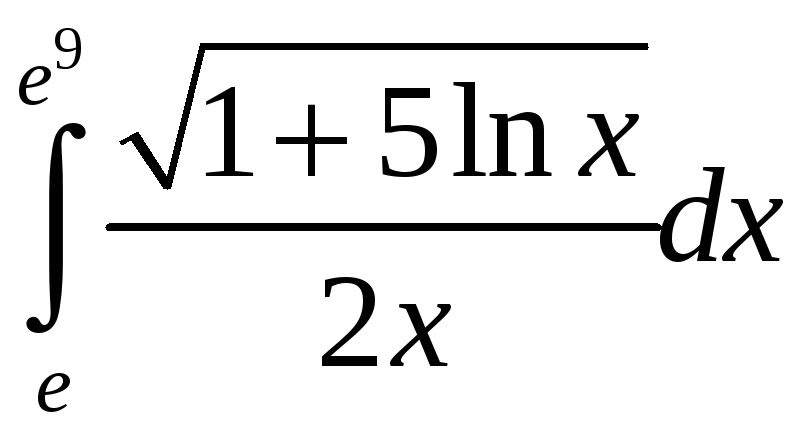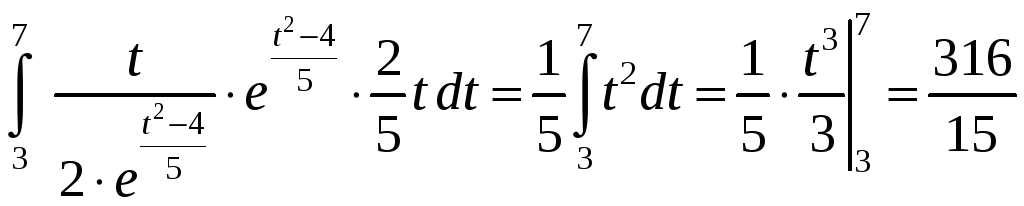б) Применим интегрирование по частям:

=

.

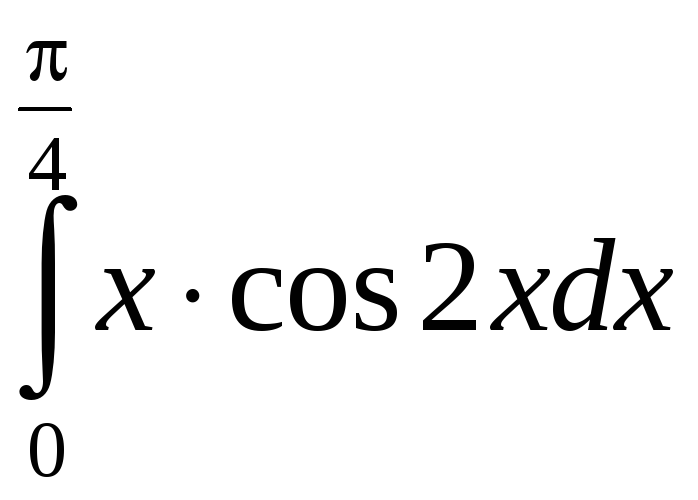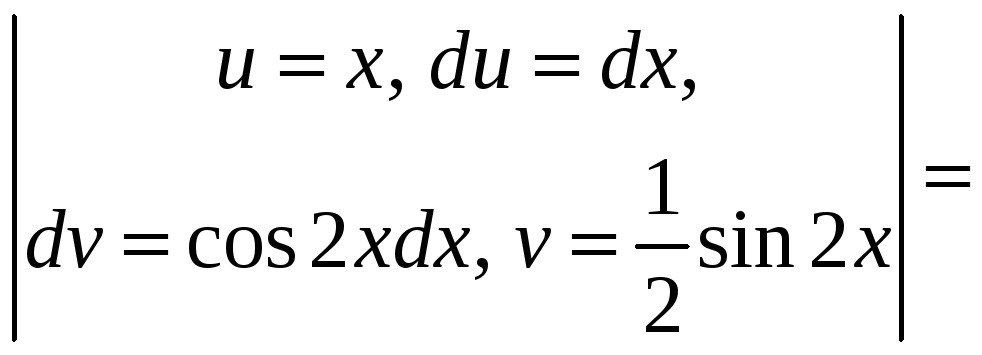
Площадь криволинейной трапеции, ограниченной графиком функции , прямыми и осью Ох (рис. 1), вычисляется по формуле (2.4).

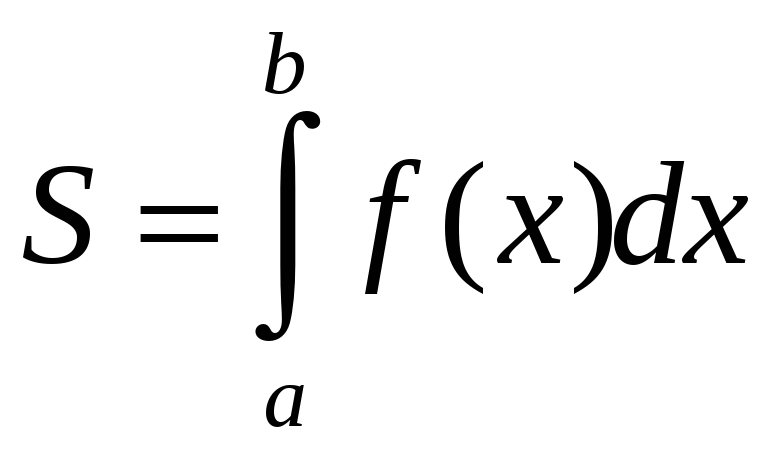. (2.4)

Если , то .

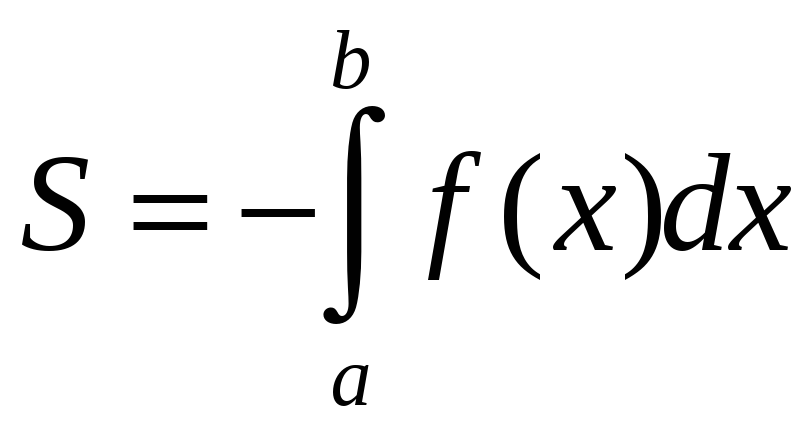Площадь плоской фигуры, изображенной на рис. 2 (здесь ), вычисляется по формуле

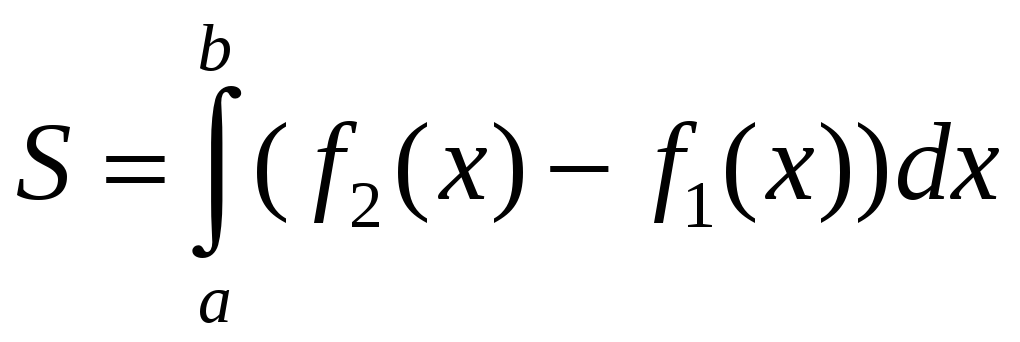. (2.5)

Y

X

Рис. 1

Y

X

Рис. 2

Пример 2.3. Вычислить площадь фигуры, ограниченной линиями .

Решение. Даны уравнения парабол и прямой. Параболы построим, приведя их уравнения к виду и . Проведя прямую , определим, площадь какой фигуры требуется вычислить (рис. 3). Ясно, что нижний предел интегрирования в этой формуле равен . Верхним пределом интегрирования будет являться абсцисса одной из точек пересечения парабол, которую найдем, решая систему

.

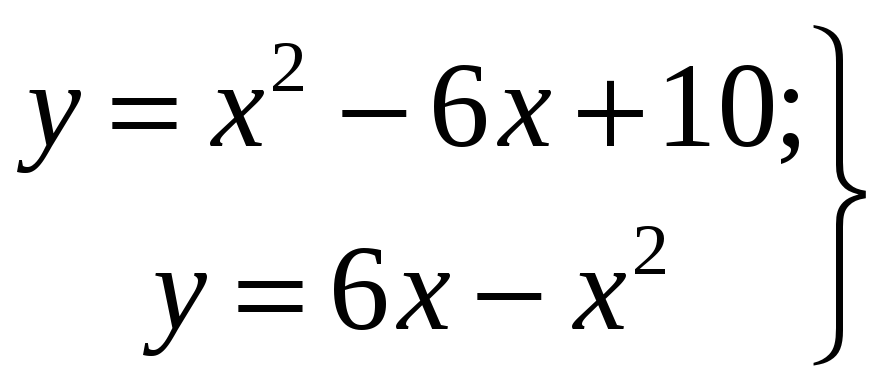
Корень последнего уравнения и есть абсцисса точки пересечения (второй корень ).

Y

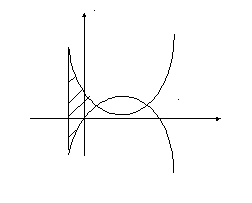
0

-1 1 3 5 X

Рис. 3

Имеем

.

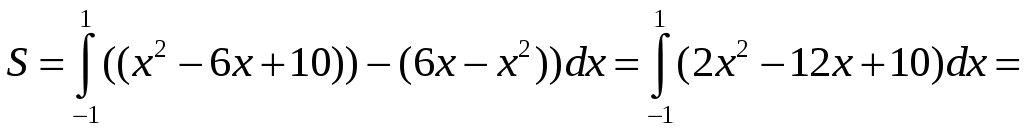
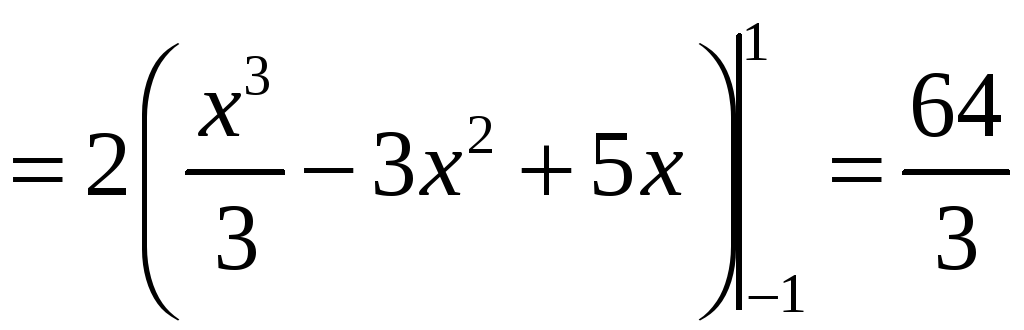Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции, которая ограничена графиком функции , прямыми и осью Ох вычисляется по формуле

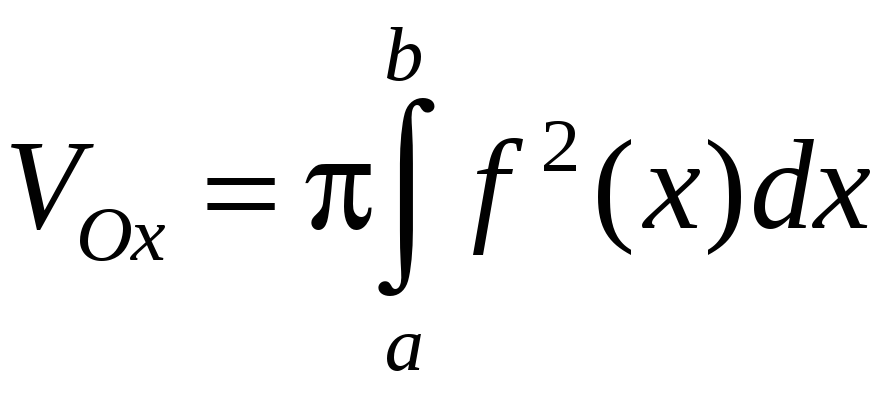. (2.6)

Если фигура, ограниченная графиком двух функций и и прямыми , вращается вокруг оси Ох, то объем тела вращения

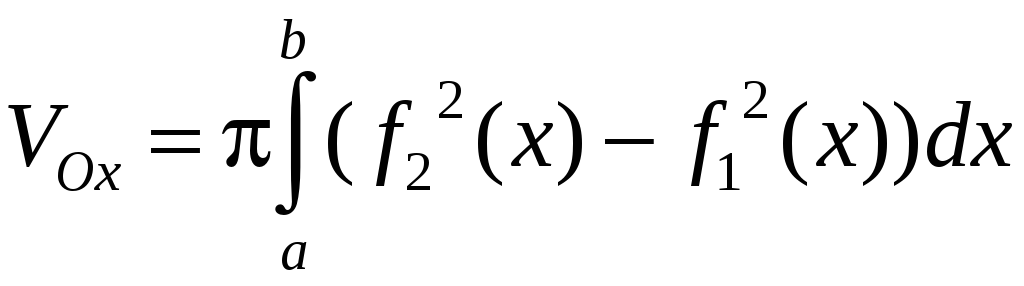. (2.7)

Пример 2.4. Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями .

Решение. Построив окружность и прямую , получим круговой сегмент (рис. 4). При вращении его вокруг оси Ох образуется тело, объем которого вычисляется по формуле (2.7), так как этот сегмент ограничен графиком двух функций и , причем . Таким образом,

=.

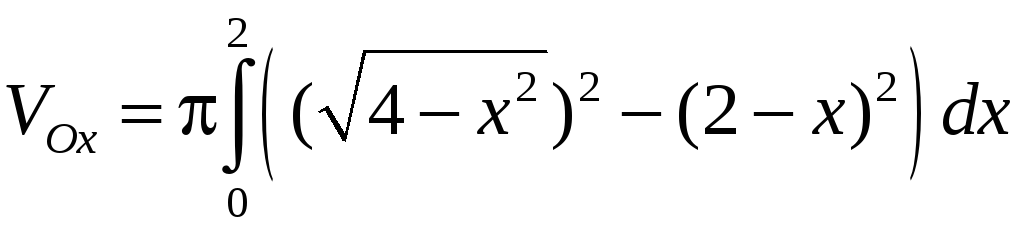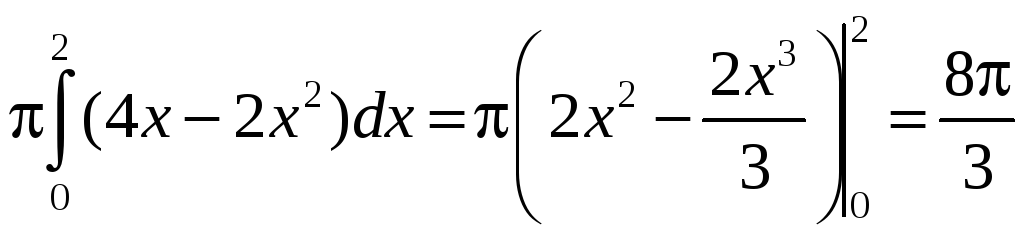Y

2

X

0 2

Рис. 4

Если плоская кривая задана уравнением , то длина ее дуги от точки А с абсциссой a до точки В c абсциссой вычисляется по формуле

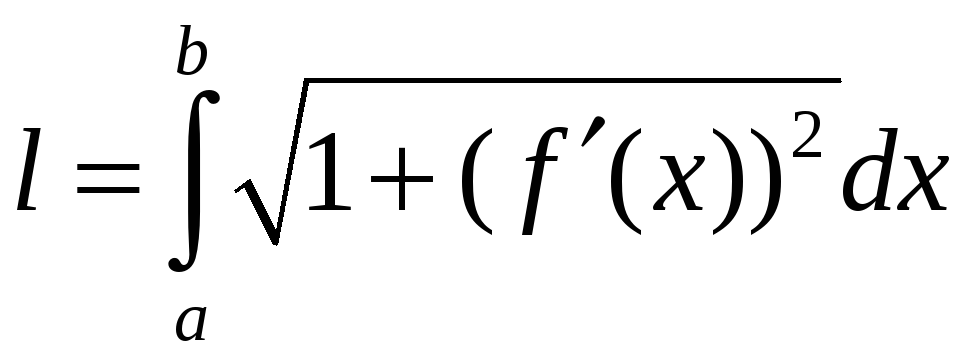. (2.8)

Если кривая задана параметрически:

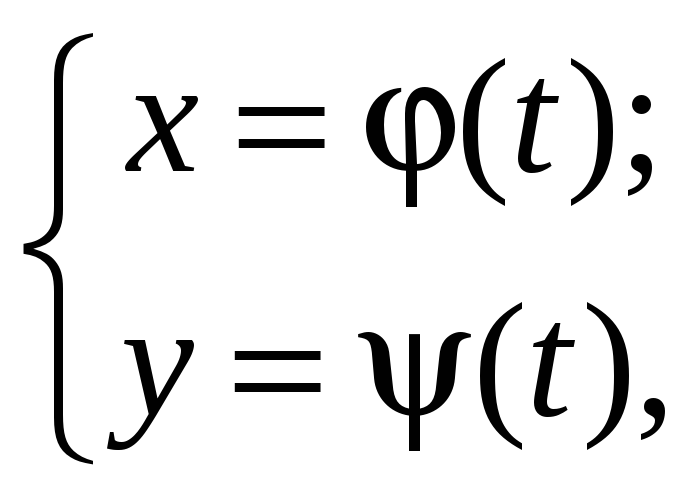
где ( значения параметра , соответствующие концам рассматриваемой дуги), то длина дуги определяется формулой

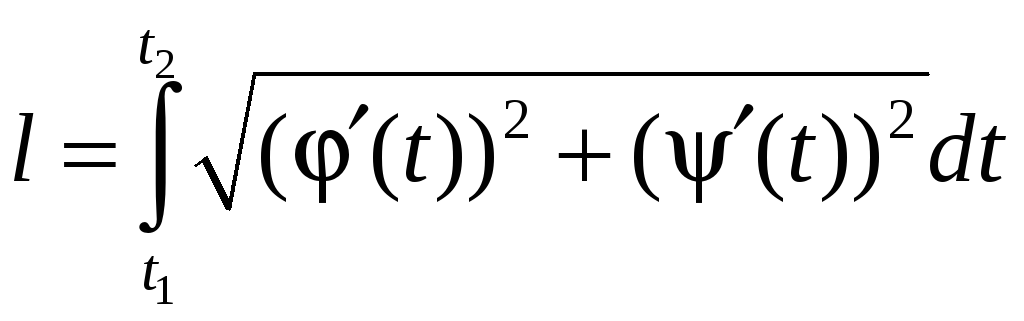. (2.9)

Пример 2.5. Вычислить длину дуги кривой, заданной уравнениями:

а) от начала координат до точки ;

б) 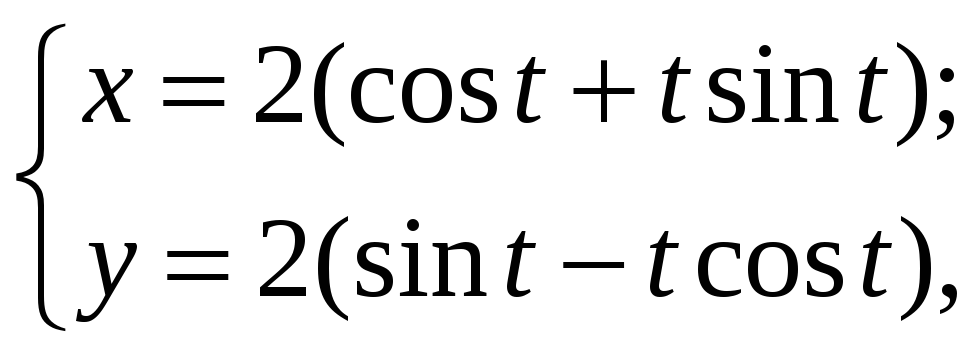при .

Решение. а) Находим .

В соответствии с формулой (2.8) (полагая в ней ) имеем:

.

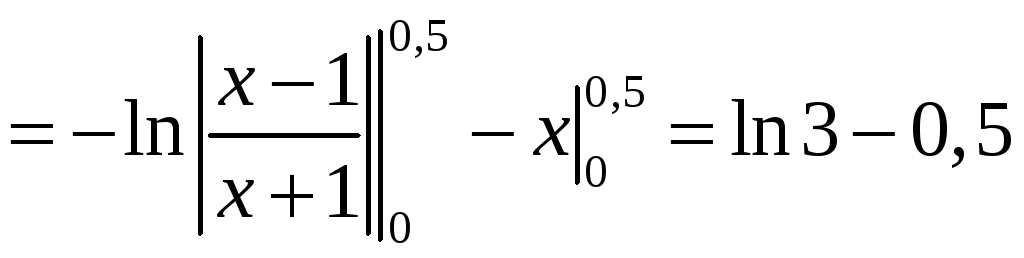б) Вычисляем

,

,

.

Согласно формуле (2.9) имеем

.
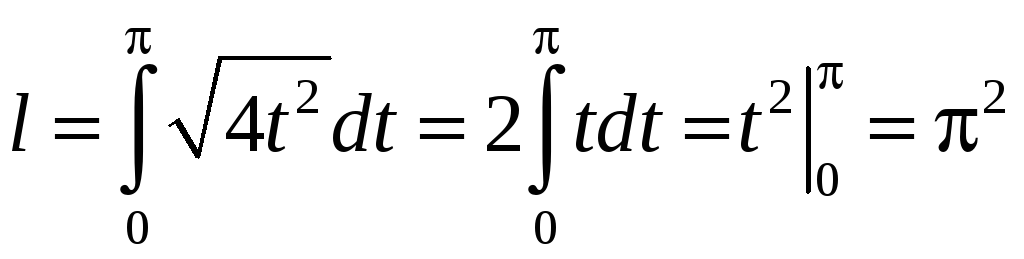