
III. Уравнения гиперболического типа
Задачу Коши для однородного волнового уравнения
![]() ,
,
удовлетворяющего начальным условиям
![]() ,
,
можно решить, используя формулу Даламбера
![]() .
.
Формула Даламбера, которая дает решения задачи Коши для неоднородного волнового уравнения с неоднородными начальными условиями имеет вид:
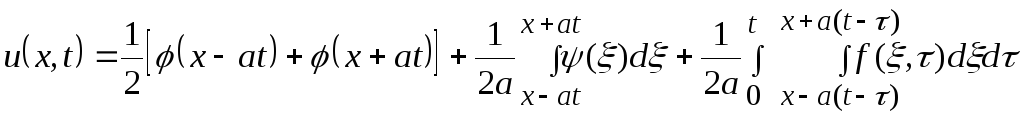 .
.
Решение краевой задачи имеет вид
![]() ,
,
где -
![]() ;
;
![]() .
.
Вариант №1
Решить задачу Коши:
-
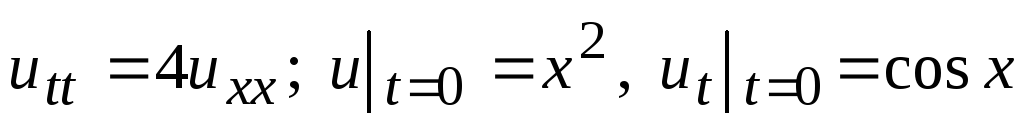 .
. -
 ;
;
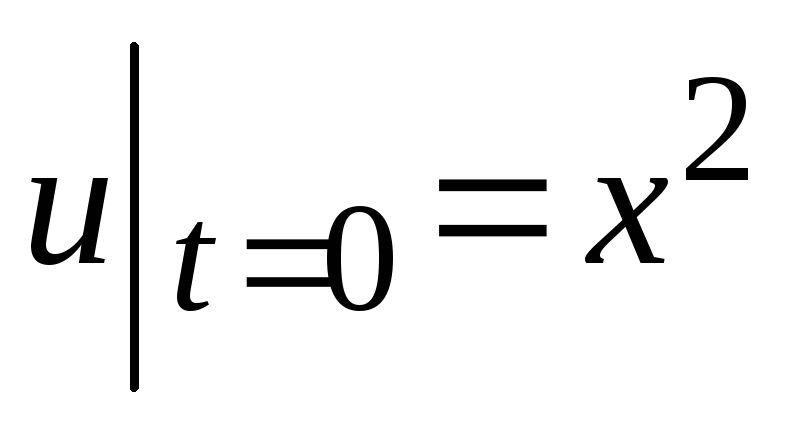 ,
,
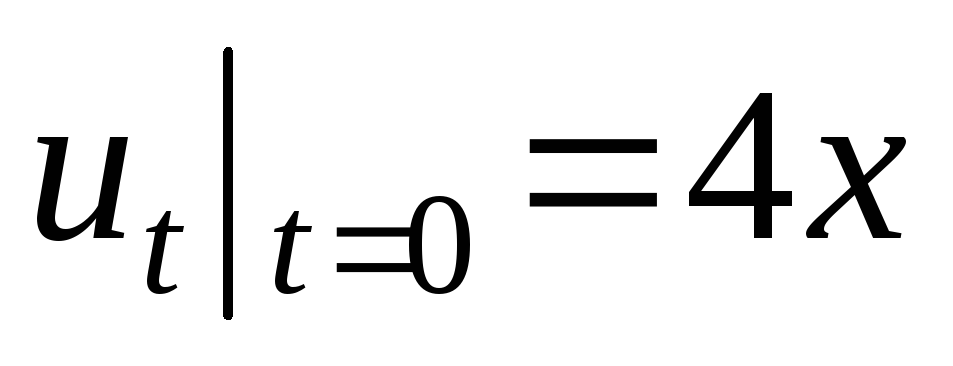 .
. -
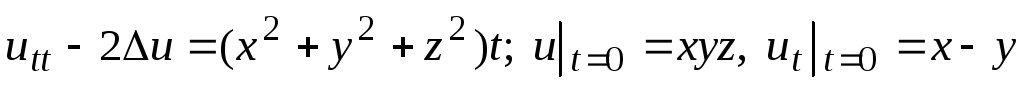 .
. -

Решить граничную задачу:
-
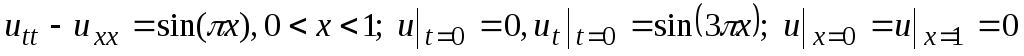 .
.
6.
![]()
Вариант №2
Решить задачу Коши:
-
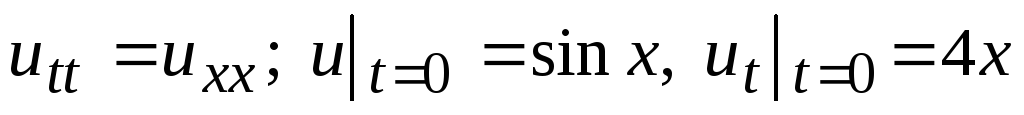 .
. -
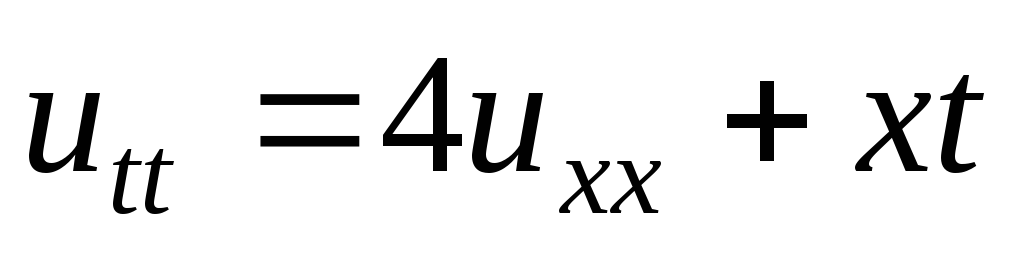 ;
;
 ,
,
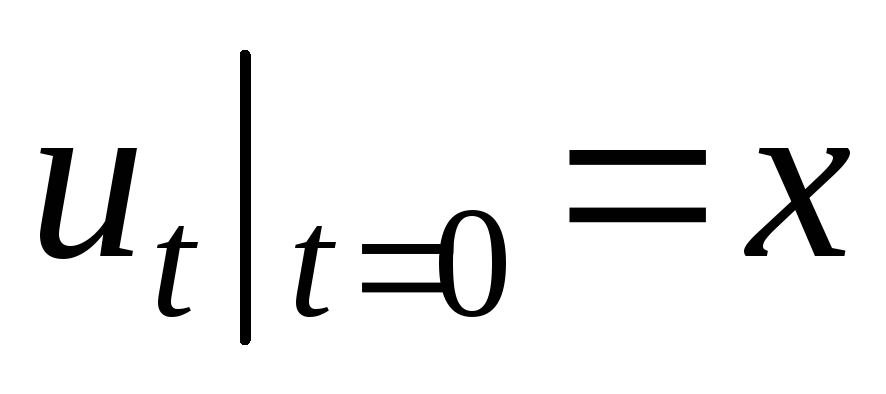 .
. -
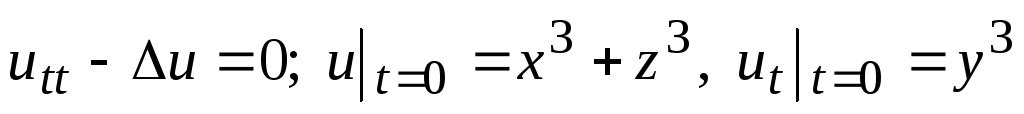 .
. -
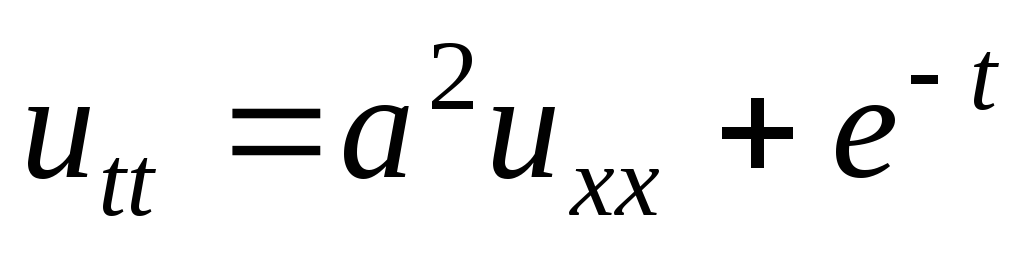 ;
;
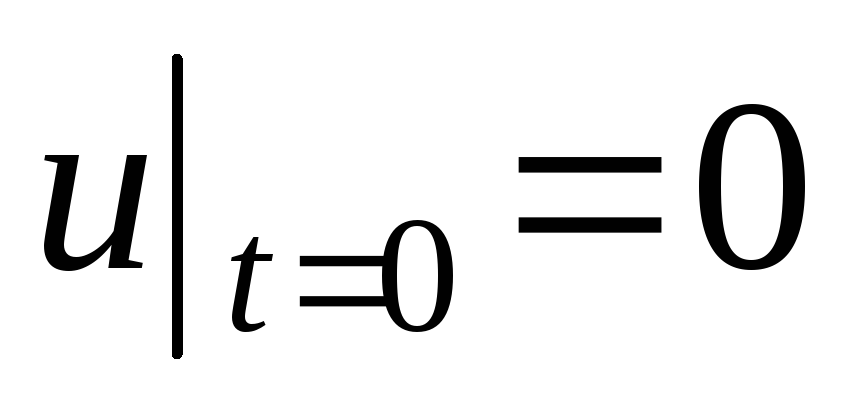 ,
,
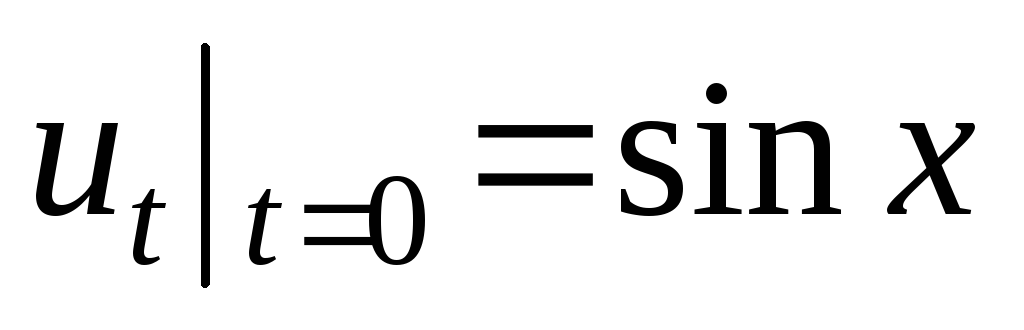 .
.
Решить граничную задачу:
-
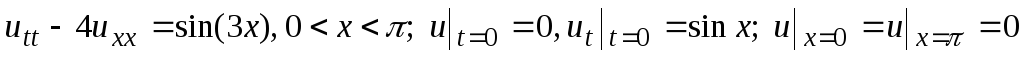 .
.
6.
![]() .
.
Вариант №3
Решить задачу Коши:
-
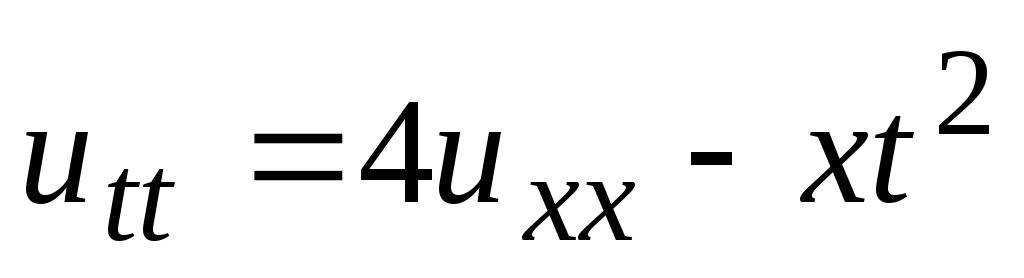 ;
;
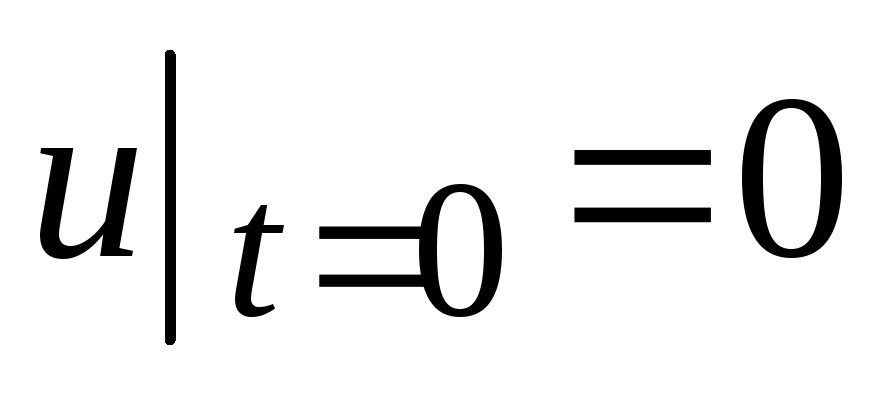 ,
,
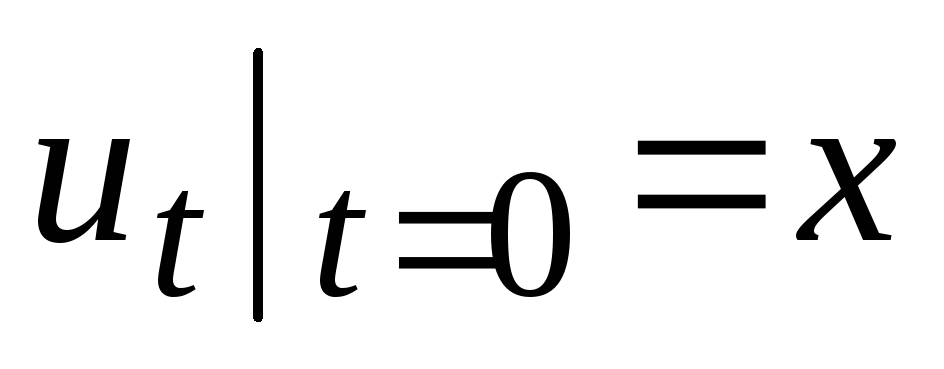 .
. -
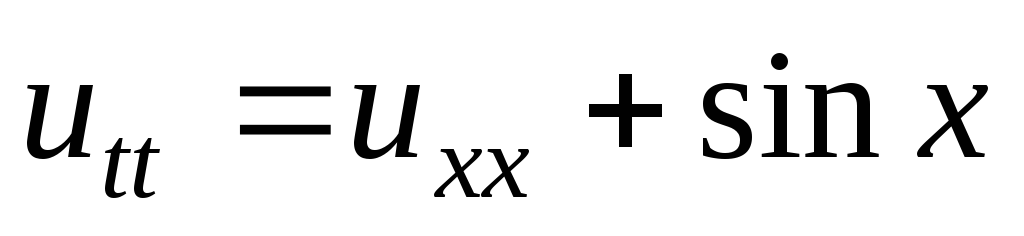 ;
;
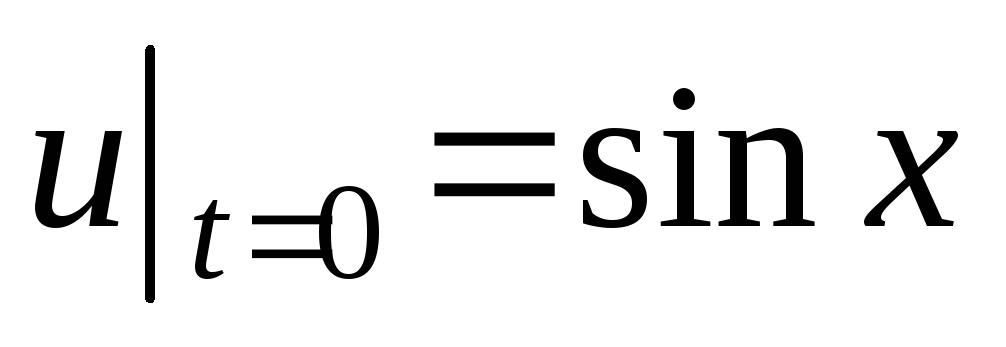 ,
,
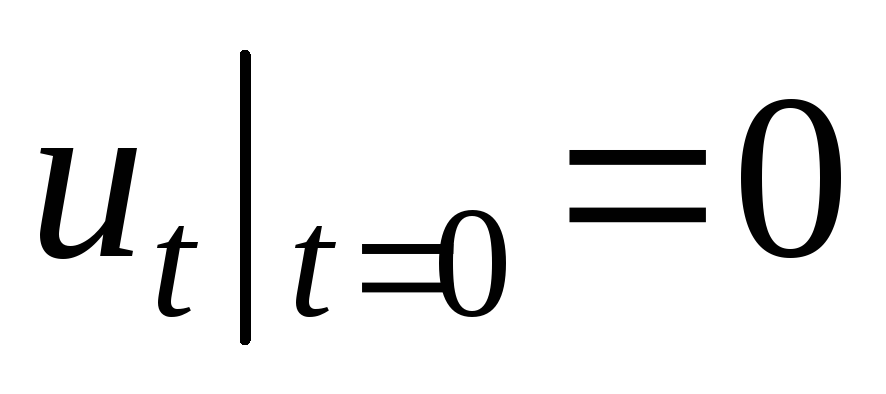 .
. -
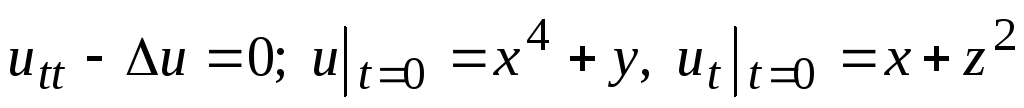 .
. -
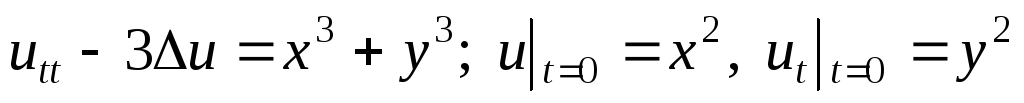
Решить граничную задачу:
5.
![]() .
.
6.
![]()
Вариант №4
Решить задачу Коши:
-
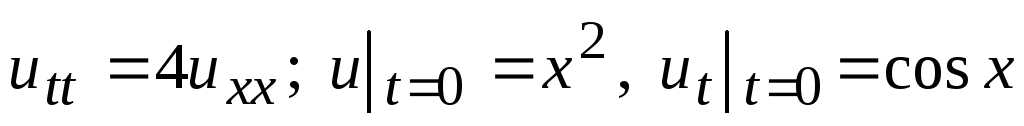 .
. -
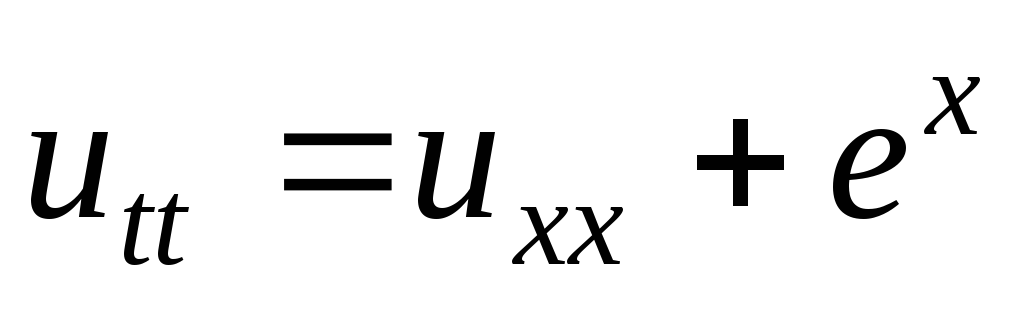 ;
;
 ,
,
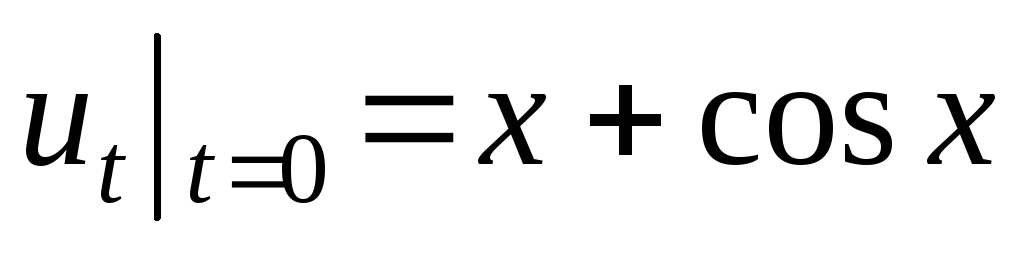 .
. -
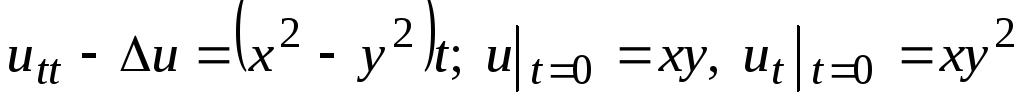 .
. -
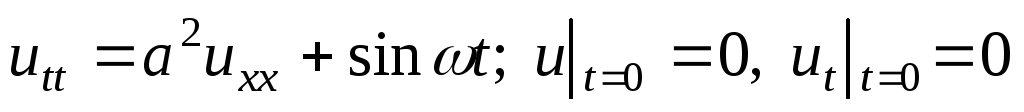
Решить граничную задачу:
5.
![]() .
.
6.
![]() .
.
Вариант №5
Решить задачу Коши:
-
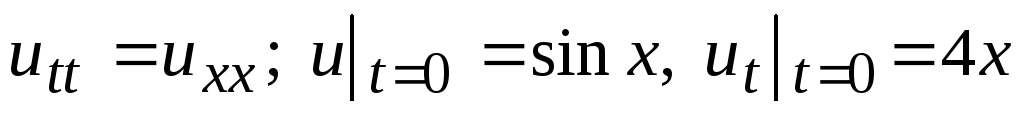 .
. -
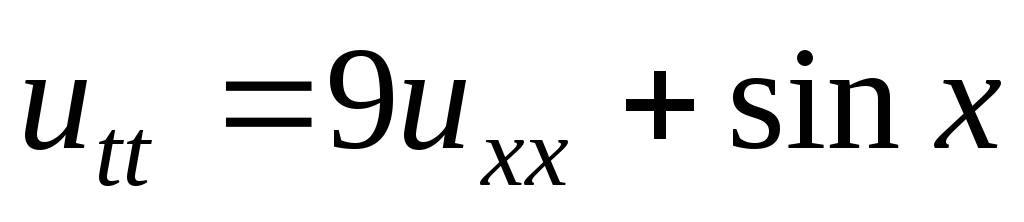 ;
;
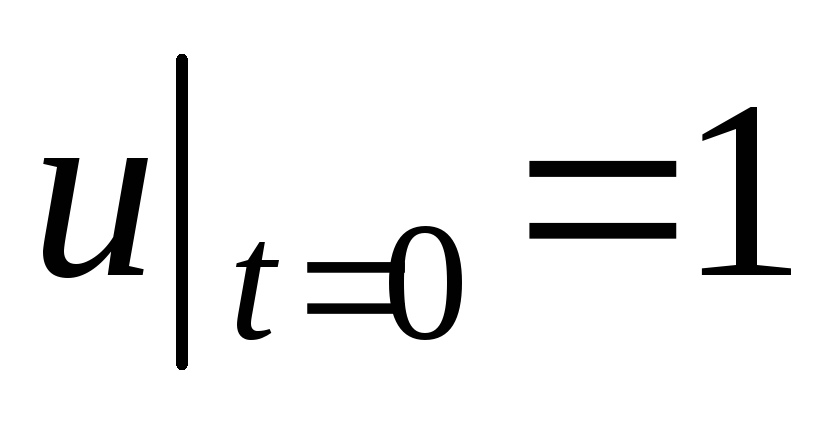 ,
,
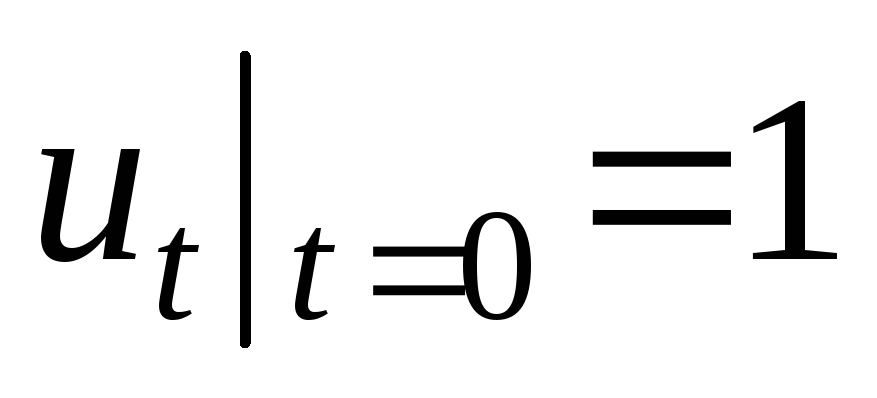 .
. -
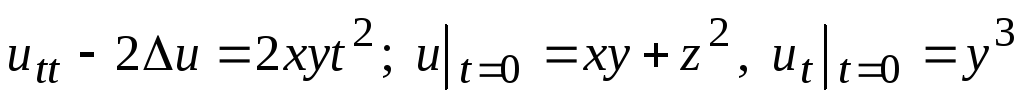 .
. -
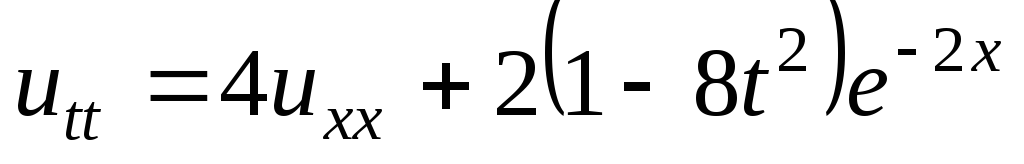 ;
;
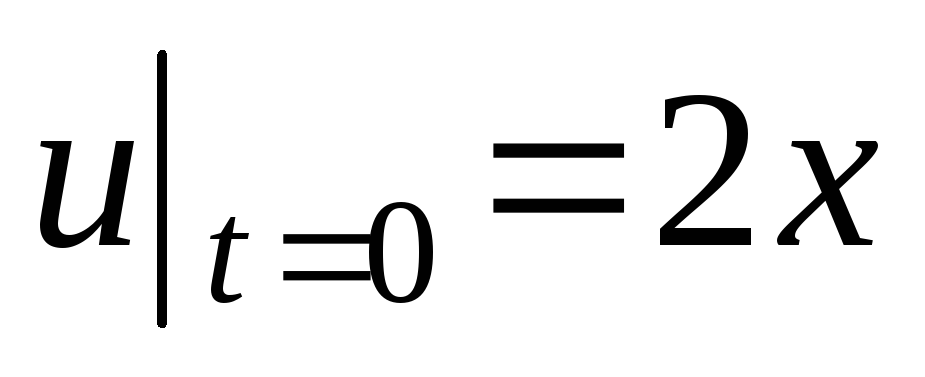 ,
,
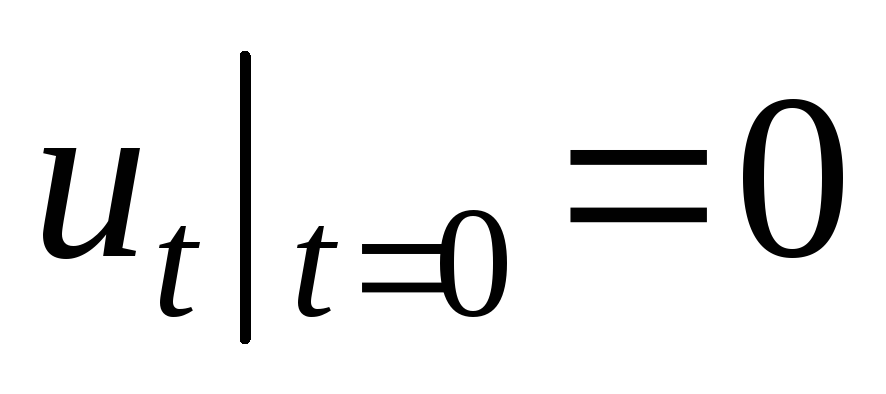 .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]() .
.
IV. Уравнения параболического типа
Задачу Коши для однородного уравнения теплопроводности.
![]() ,
,
удовлетворяющего неоднородному начальному условию
![]() ,
,
можно решить, используя формулу Пуассона
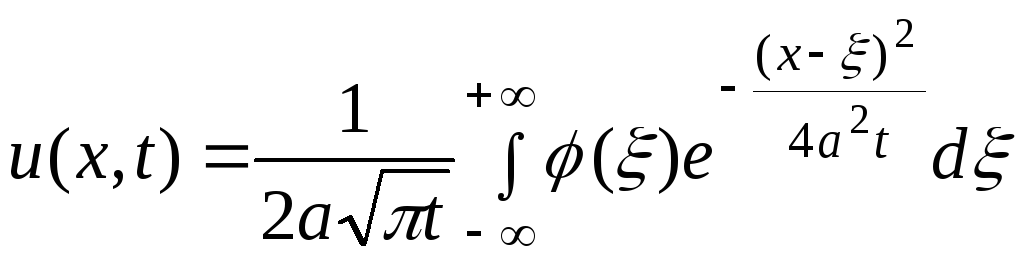 .
.
Решение задачи Коши для неоднородного уравнения теплопроводности
![]() ,
,
удовлетворяющее неоднородному начальному условию
![]() ,
,
определяется формулой
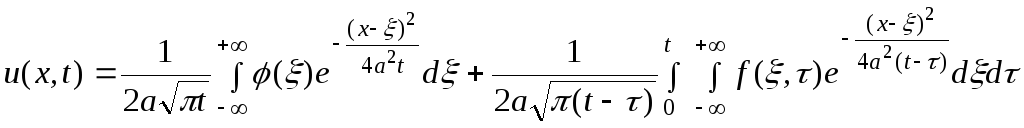 .
.
Решение однородного линейного параболического уравнения
![]() ,
,
удовлетворяющее при t=0 начальному условию
![]() ,
,
и однородным граничным условиям вида
![]()
определяется формулой
![]() ,
,
где
![]() .
.
Решение однородного линейного параболического уравнения
![]() ,
,
удовлетворяющее при t=0 начальному условию
![]() ,
,
и однородным граничным условиям вида
![]()
определяется формулой
![]() ,
,
где
![]() .
.
Решение однородного линейного параболического уравнения
![]() ,
,
удовлетворяющее при t=0 начальному условию
![]() ,
,
и однородным граничным условиям вида
![]()
определяется формулой
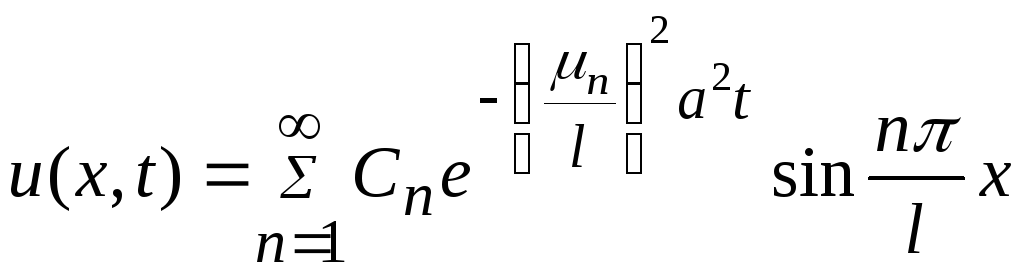 ,
,
где
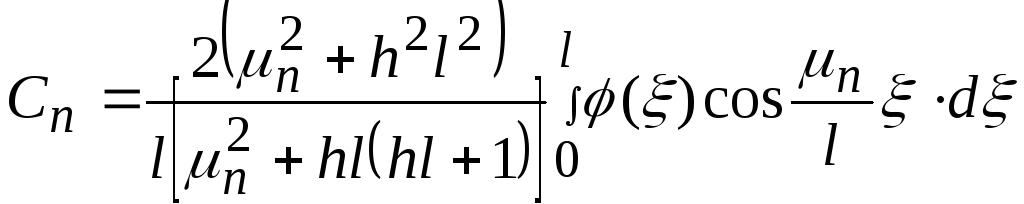 ,
,
Значения
![]() являются действительными положительными
корнями трансцендентного уравнения:
являются действительными положительными
корнями трансцендентного уравнения:
![]() .
.
Решение задачи для неоднородного уравнения теплопроводности
![]() ,
,
с начальными условиями
![]() ,
,
и граничными условиями вида
![]() .
.
Определяется формулой
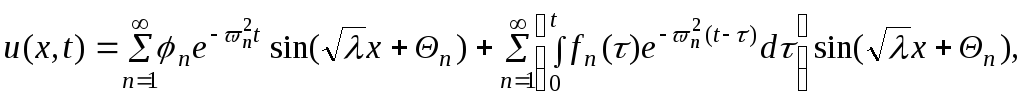
где
-
![]() ,
а
,
а
![]() определяются из значений общего вида
краевых условий-
определяются из значений общего вида
краевых условий-![]() ;
;
![]() ;
;
![]() ;
;
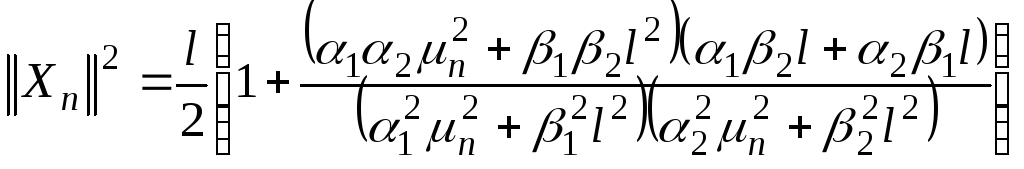 .
.
Решение смешанной краевой задачи определяется формулой
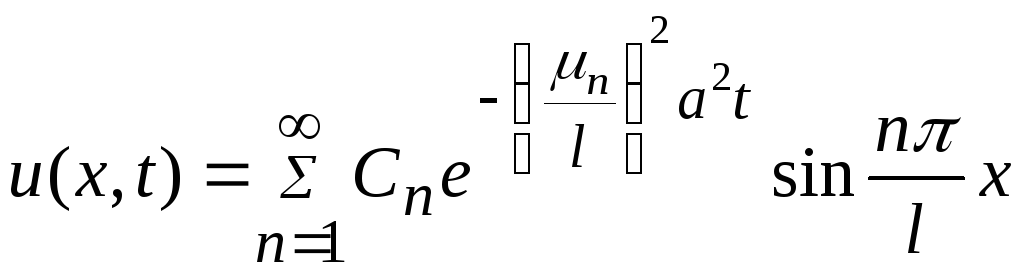 ,
,
где
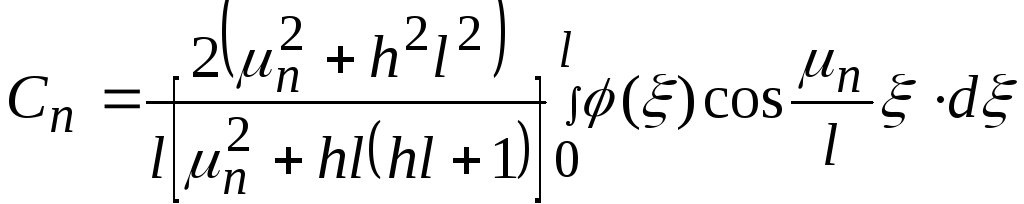 .
.
Вариант №1
Решить задачу Коши:
-
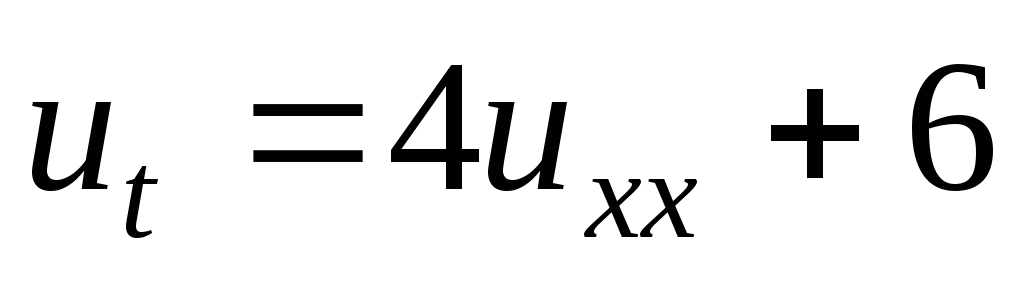 ;
;
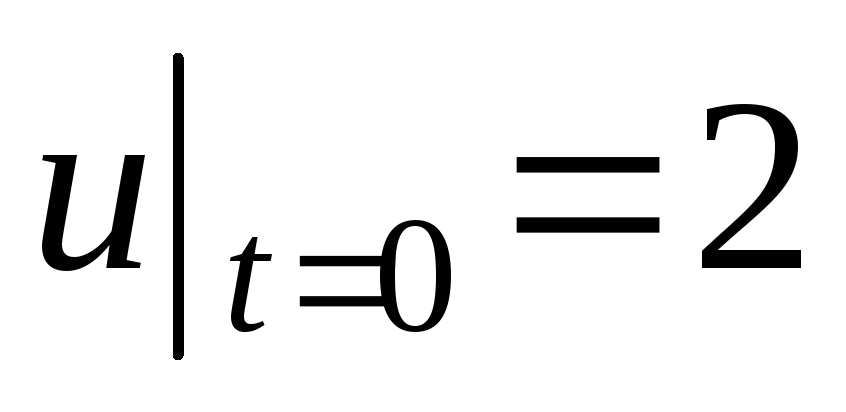 .
.
-
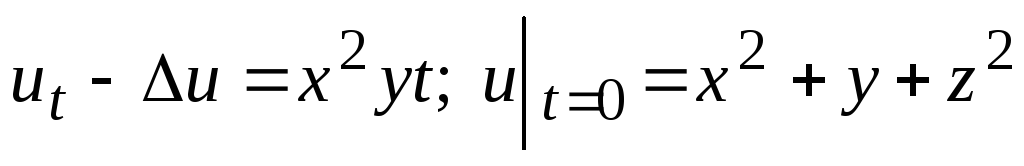 ;
; -
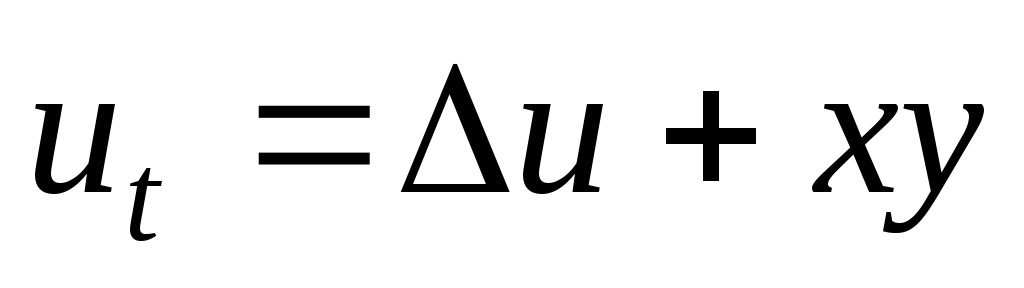 ;
;
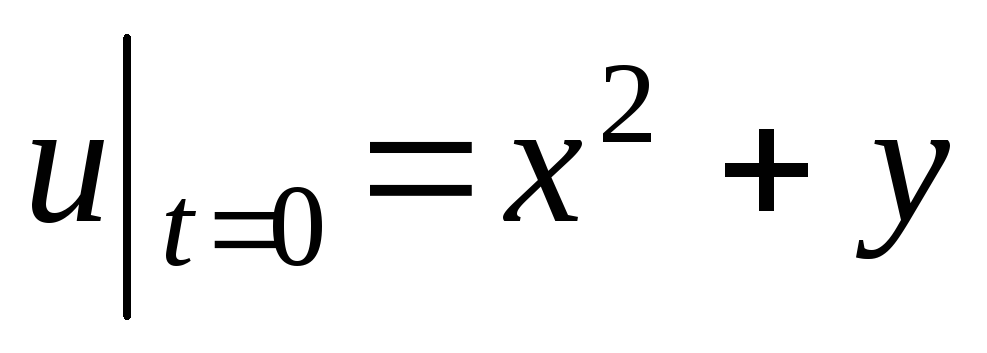 ;
;
Решить граничную задачу:
-
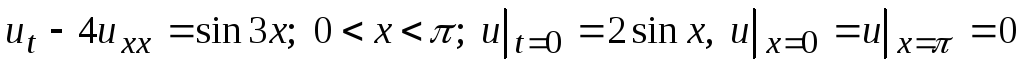 ;
; -
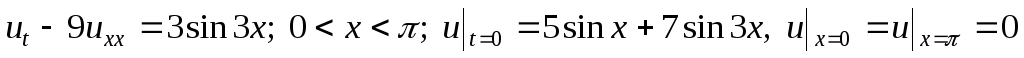 .
.
Вариант №2
Решить задачу Коши:
-
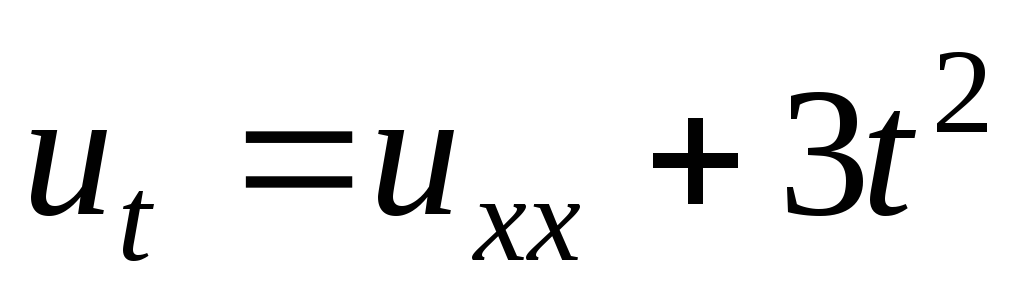 ;
;
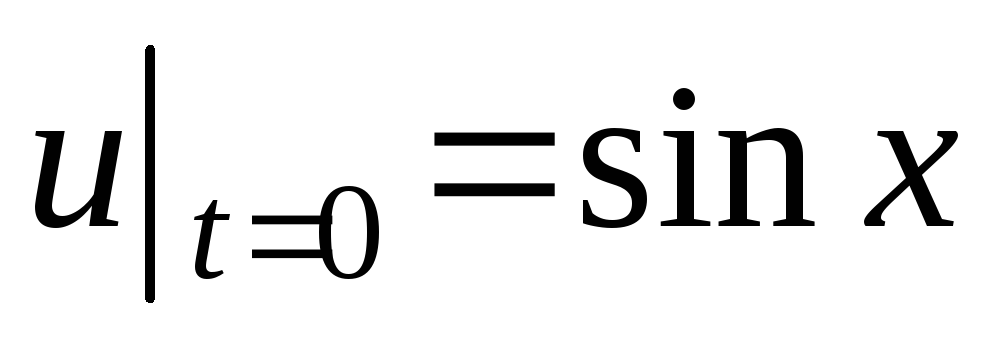 .
. -
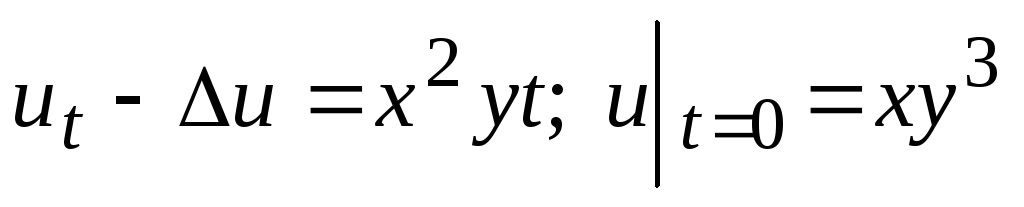 .
. -
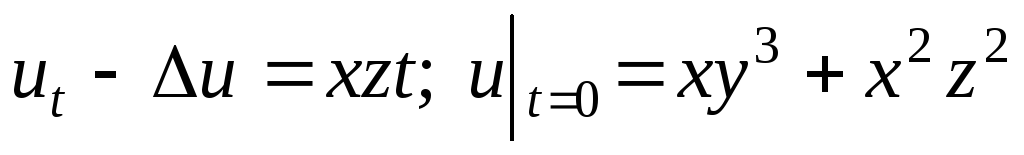 ;
;
Решить граничную задачу:
-
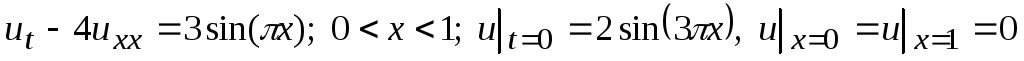 .
.
5.
![]() .
.
Вариант №3
Решить задачу Коши:
-
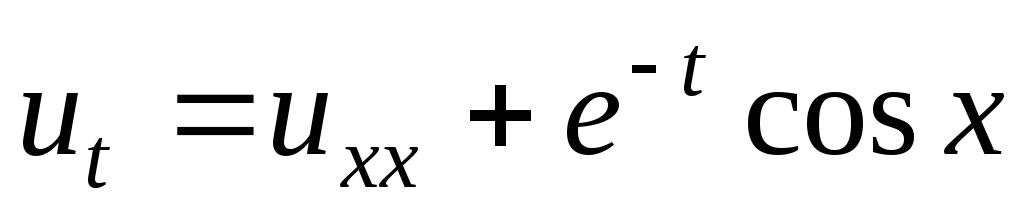 ;
;
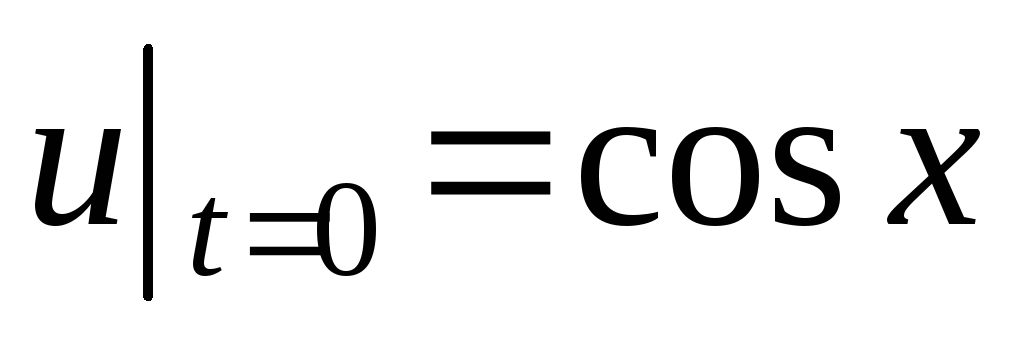 .
.
-
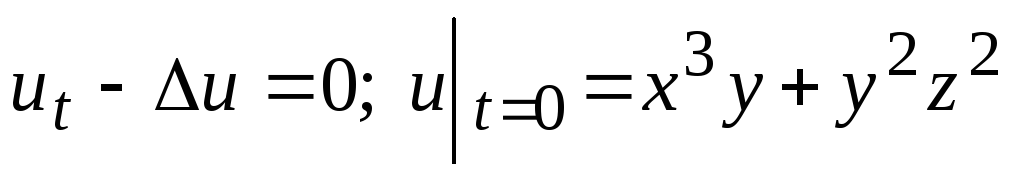 .
.
-
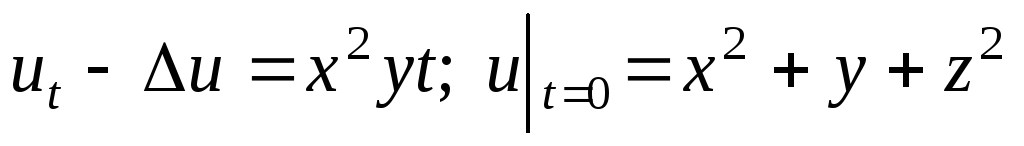 ;
;
Решить граничную задачу:
-
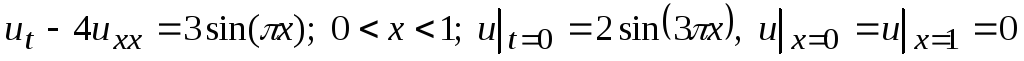 .
. -
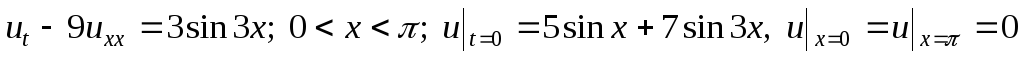
Вариант №4
Решить задачу Коши:
-
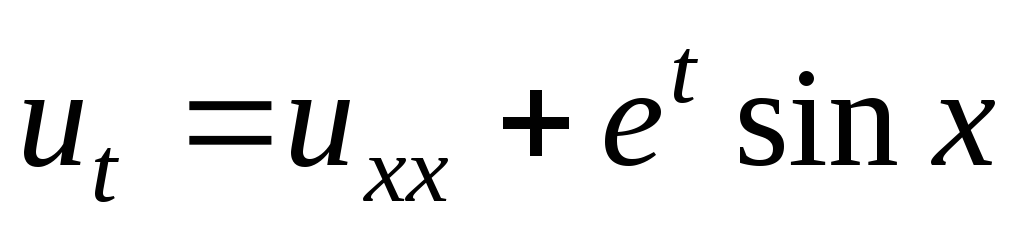 ;
;
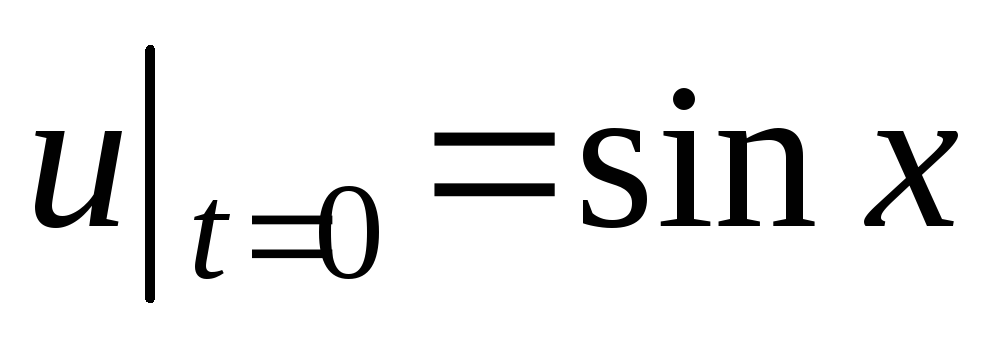 .
.
-
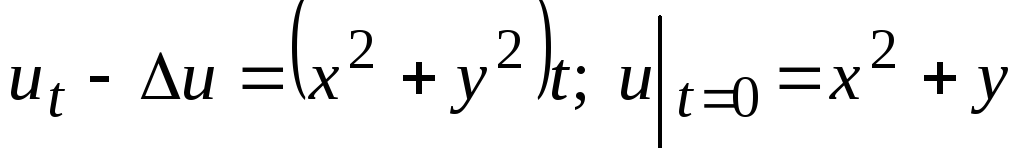 .
. -
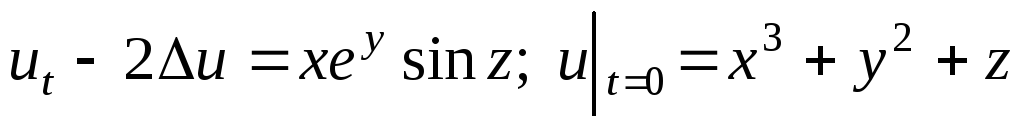 .
.
Решить граничную задачу:
-
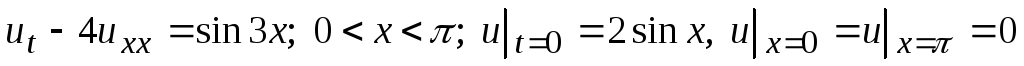 ;
; -
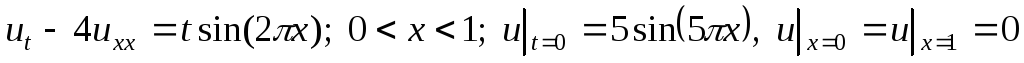
Вариант №5
Решить задачу Коши:
-
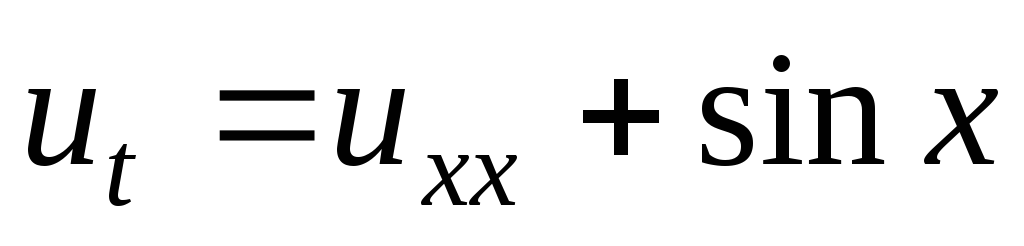 ;
;
 .
. -
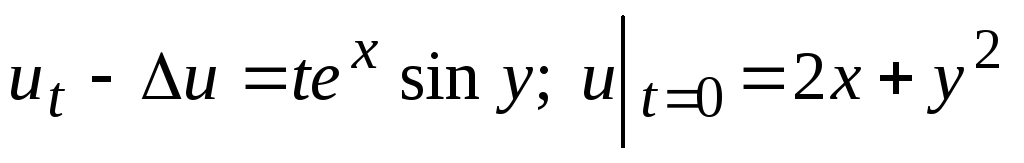 .
. -
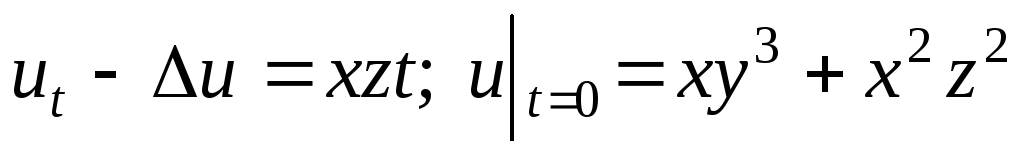 .
.
Решить граничную задачу:
-
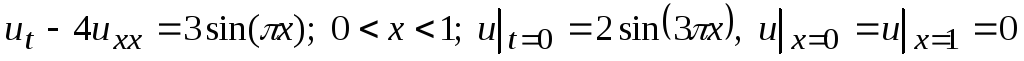 .
. -
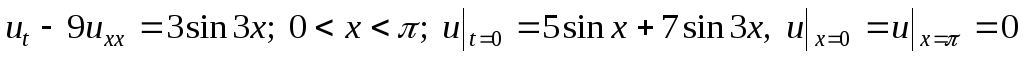 .
.
V. Уравнения эллиптического типа
Решение первой, второй и третьей краевых задач для уравнения Лапласа в круге имеет вид:
-
Задача Дирихле:
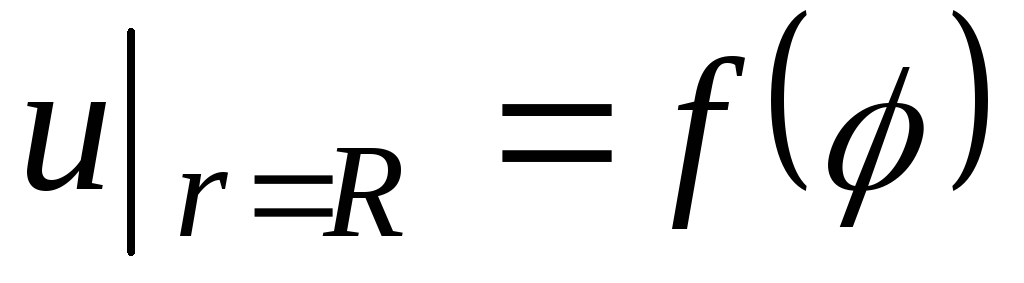 ,
,
![]() .
.
или
![]() .
.
-
Задача Неймана:
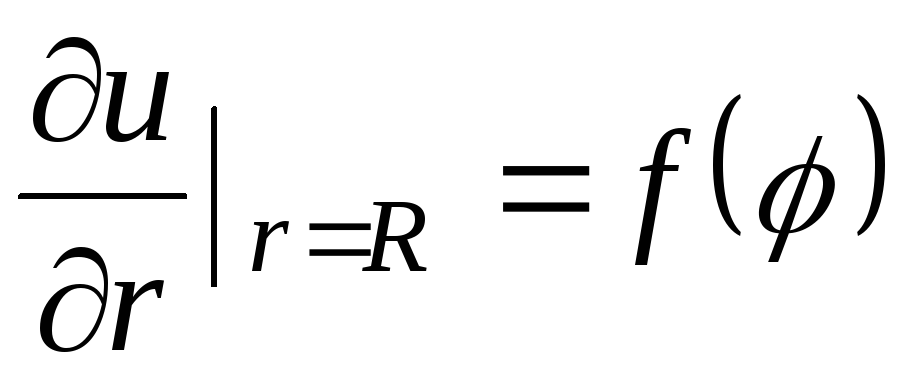 ,
,
![]() .
.
где С – произвольная постоянная.
-
Третья краевая задача:
![]() ,
,
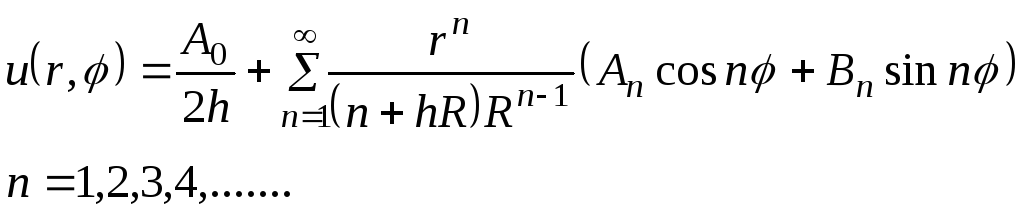
Коэффициенты
![]() в решениях являются коэффициентами
Фурье функции
в решениях являются коэффициентами
Фурье функции
![]() и
определяются по формулам
и
определяются по формулам
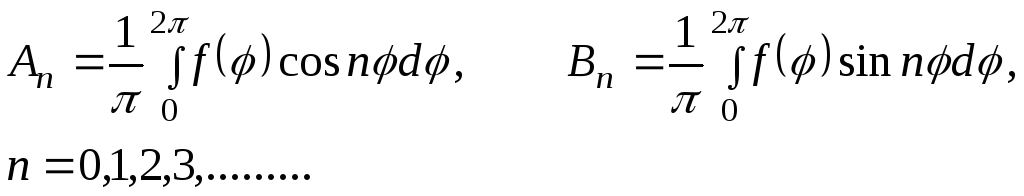
Решение первой, второй и третьей краевых задач для уравнения Лапласа вне круга имеют вид:
1. Задача Дирихле:
![]() ,
,
![]() .
.
2. Задача Неймана:
![]() ,
,
![]() .
.
3. Третья краевая задача:
![]() ,
,
![]()
Коэффициенты
![]() в решениях являются коэффициентами
Фурье функции
в решениях являются коэффициентами
Фурье функции
![]() и
определяются по формулам
и
определяются по формулам
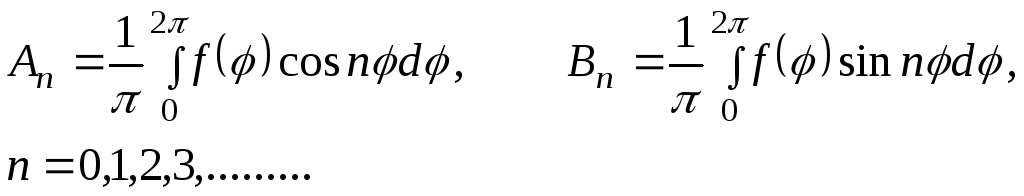
Вариант №1
-
Найти функцию, гармоническую внутри единичного круга и такую, что
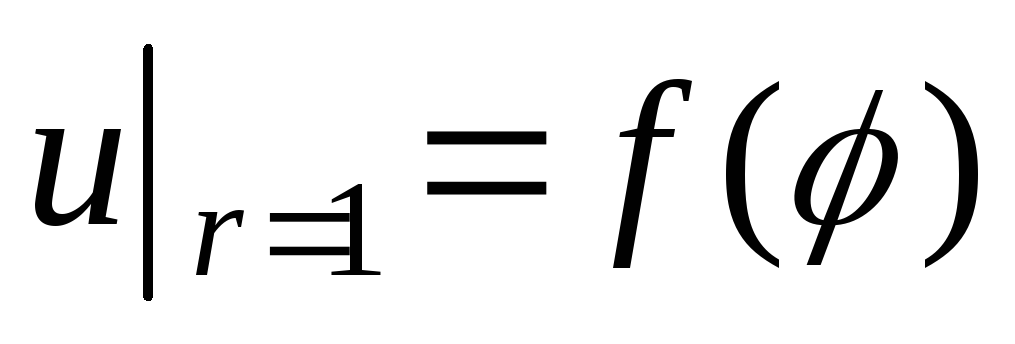 ,
где:
,
где:
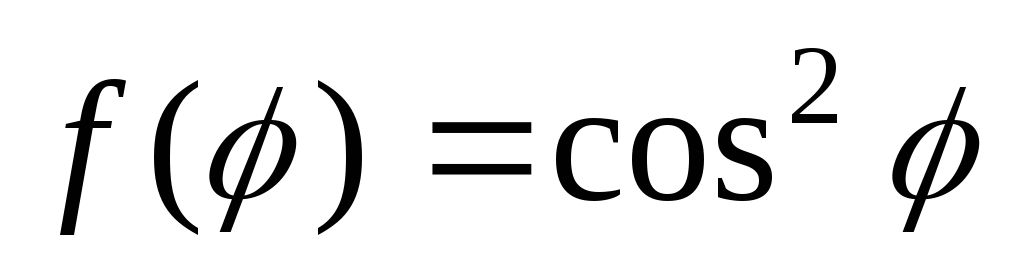 .
. -
Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
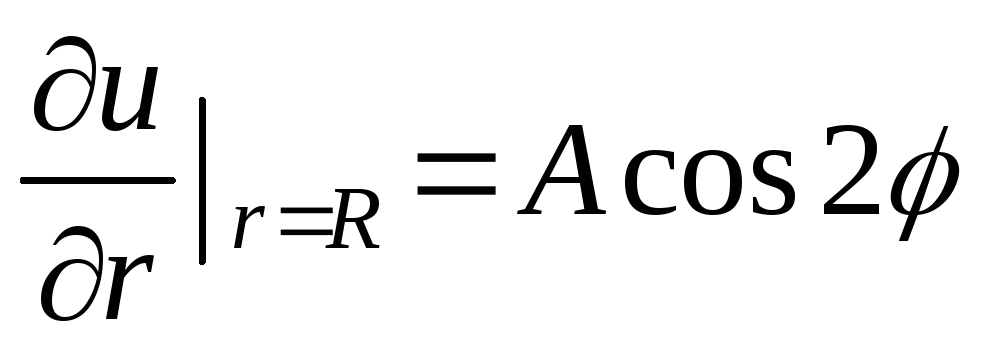 .
. -
Решить уравнение Лапласа в круге:
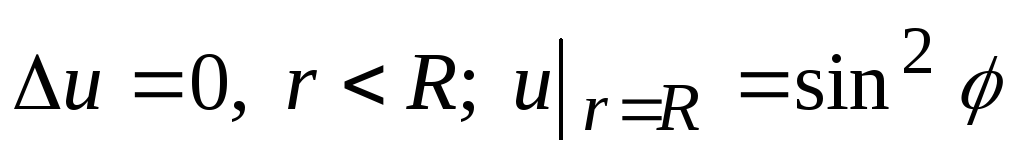 .
. -
Решить уравнение Лапласа вне круга:
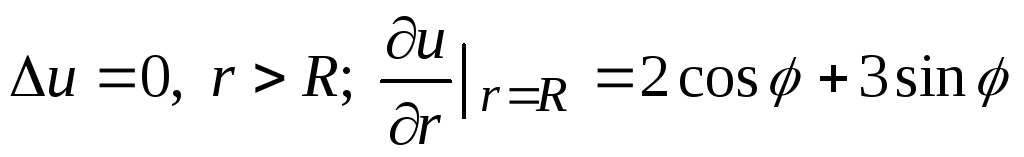 .
.
Вариант №2
-
Найти функцию, гармоническую внутри единичного круга и такую, что
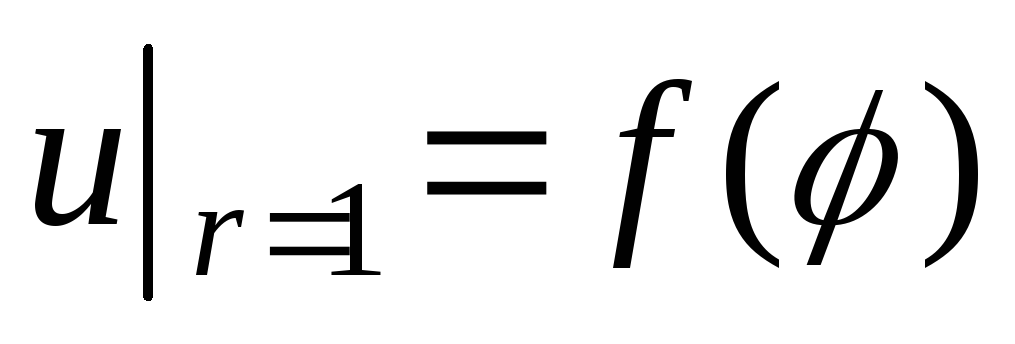 ,
где:
,
где:
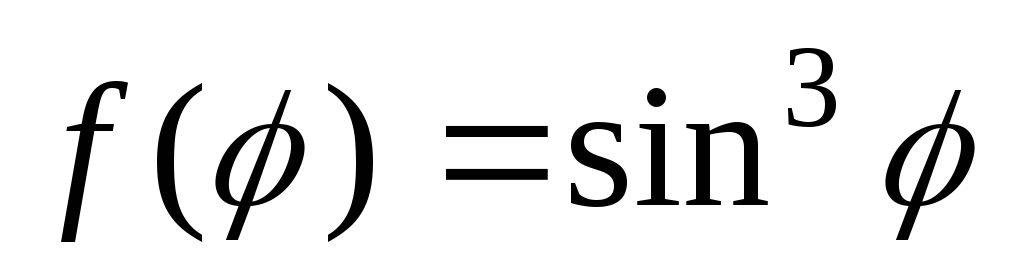 .
. -
Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
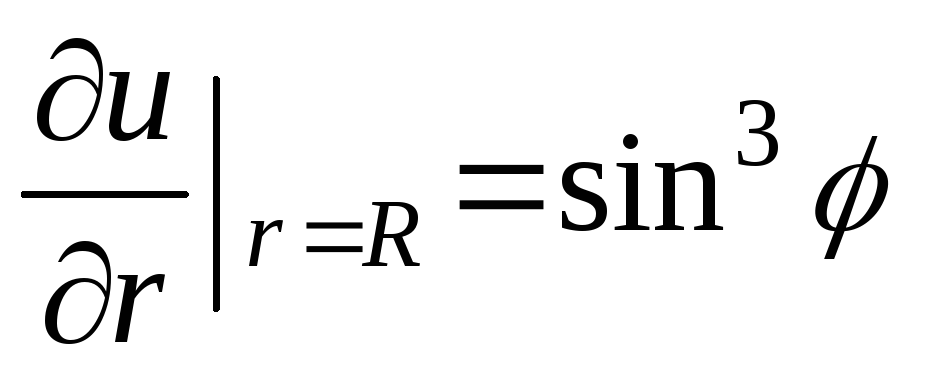 .
. -
Решить уравнение Лапласа вне круга:
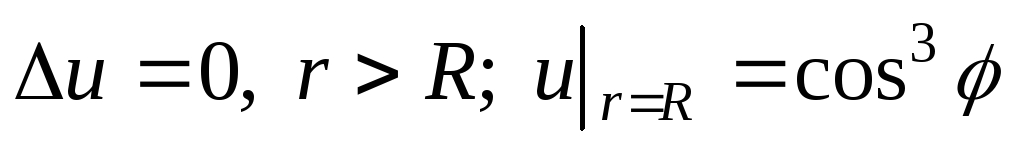 .
. -
Решить уравнение Лапласа в круге:
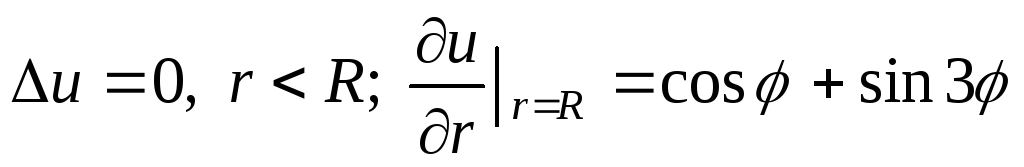 .
.
Вариант №3
-
Найти функцию, гармоническую внутри единичного круга и такую, что
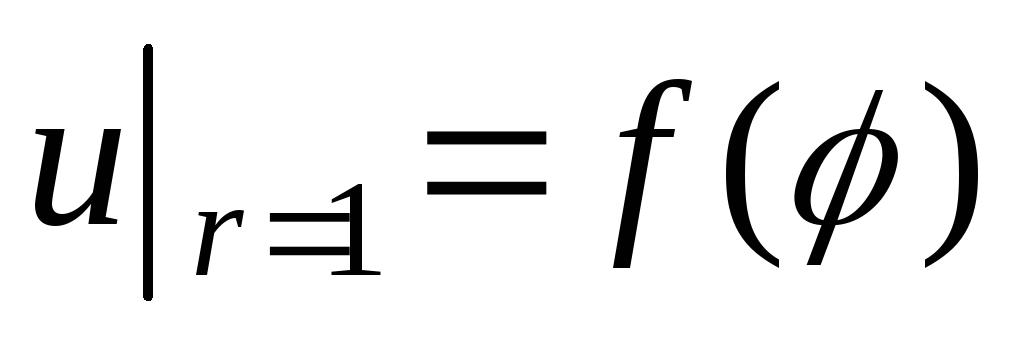 ,
где:
,
где:
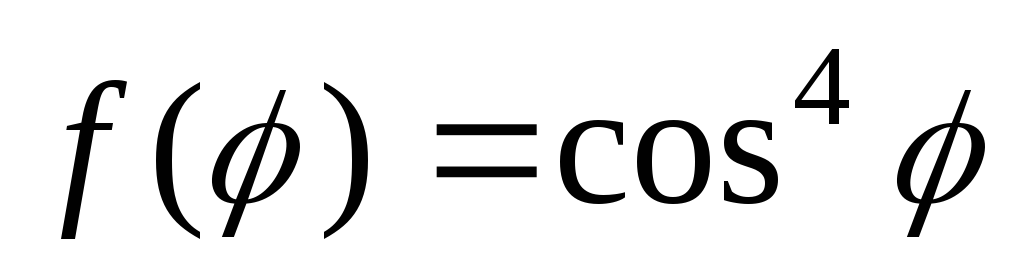 .
. -
Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что

-
Решить уравнение Лапласа вне круга:
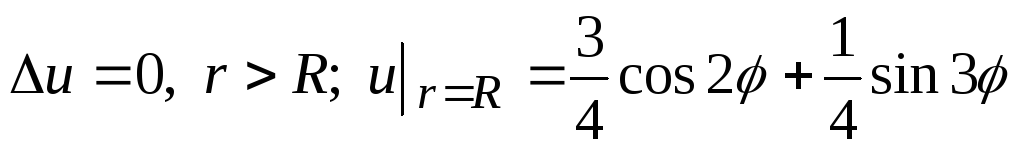 .
. -
Решить уравнение Лапласа в круге:
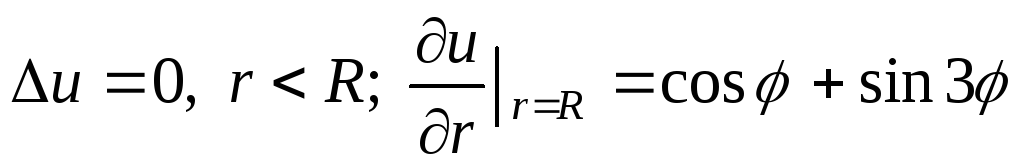 .
.
Вариант №4
-
Найти функцию, гармоническую внутри единичного круга и такую, что
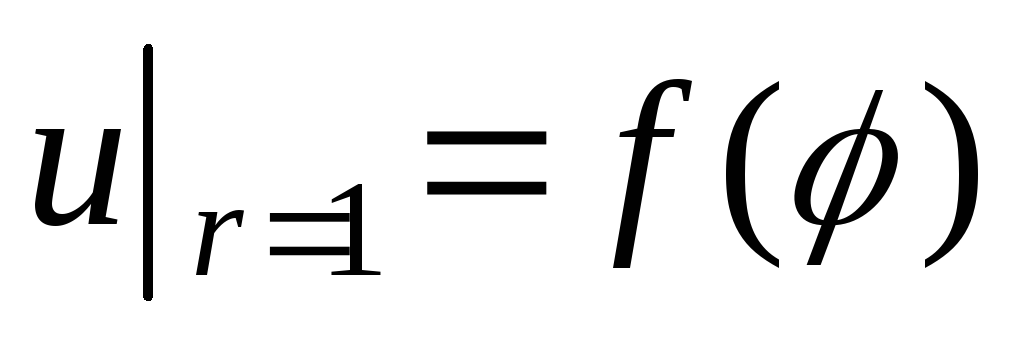 ,
где:
,
где:
 .
. -
Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
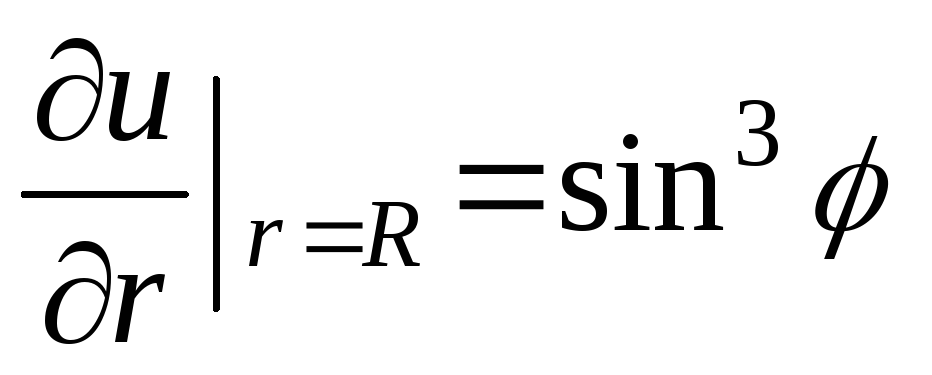 .
. -
Решить уравнение Лапласа в круге:
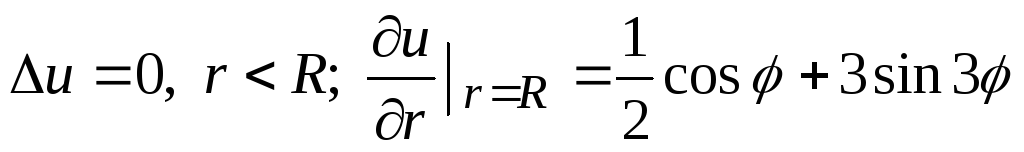 .
. -
Решить уравнение Лапласа вне круга:
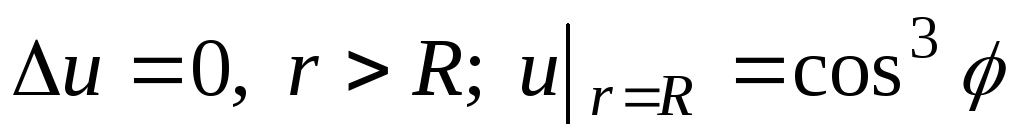
Вариант №5
-
Найти функцию, гармоническую внутри единичного круга и такую, что
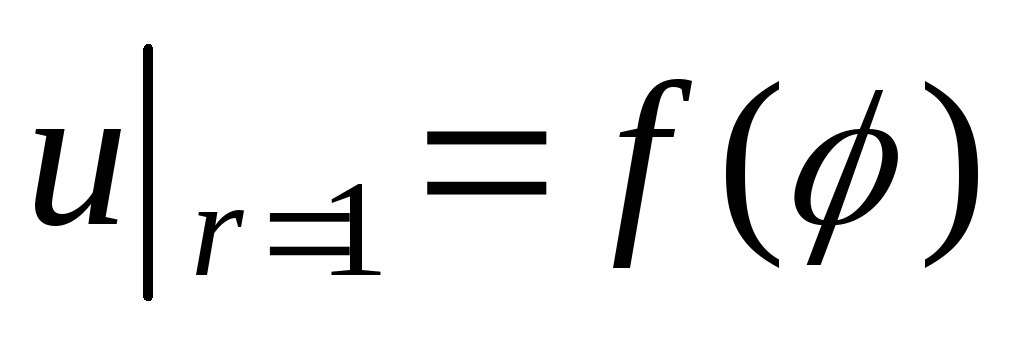 ,
где:
,
где:
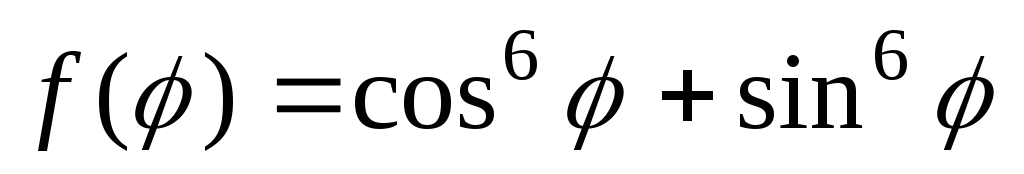 .
. -
Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
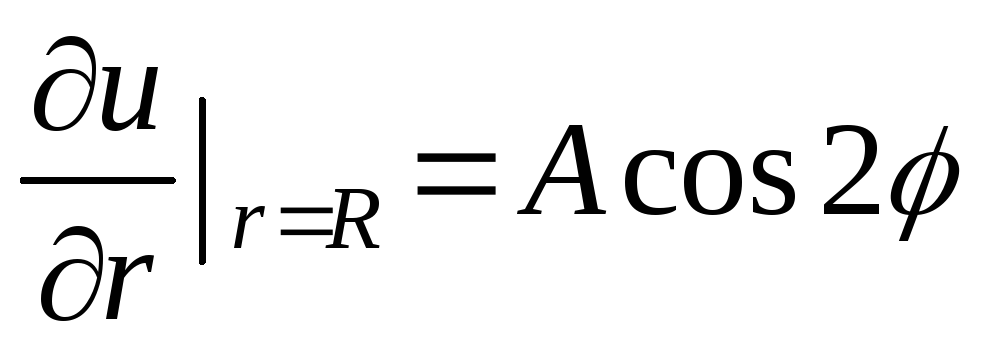
-
Решить уравнение Лапласа в круге:
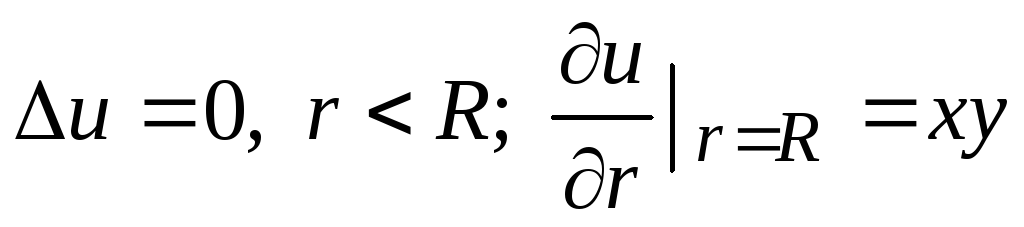 .
. -
Решить уравнение Лапласа вне круга:
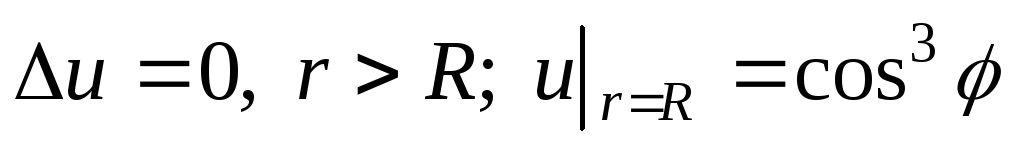 .
.
Методические указания составил Терещенко С.В. - заведующий кафедрой физики горных процессов и геофизики.
