Приклади виконання завдання с-5.

Задача 1.

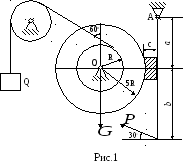
Визначити мінімальне значення сили Р і реакції опор системи, що знаходиться в стані спокою (рис.1). G=2 кН; Q=20 кН; a=0,2 м; b=0,8 м; c =0,05 м; f = 0,5. Розв’язання. Звільнимо систему від в’язей, замінивши їх дію реакціями в’язей. Реакції нерухомих циліндричних шарнірів: в точці О - , ; в точці А - , . Реакція нитки напрямлена уздовж нитки і чисельно дорівнює вазі тіла прив’язаного до нитки.

Отримали довільну плоску систему сил, яка містить п’ять невідомих сил (рис.2). Розчленуємо систему на окремі тіла: барабан і гальмівний пристрій (рис.3). При розчленуванні скористаємося аксіомою взаємодії, згідно з якою: , , , . При прикладанні сили тертя до барабана слід мати на увазі, що вона заважає обертанню барабана. В стані граничної рівноваги сила мінімальна, а сила тертя між гальмівним пристроєм і барабаном визначається рівністю: .

На кожну частину системи діє довільна плоска система сил. Складемо для кожної частини системи по три рівняння рівноваги.

Ліва частина – барабан:

(1)

(2)

(3)

Права частина – гальмівний пристрій:

(4)

(5)

(6)

Розв’язуємо ці рівняння і знаходимо шукані величини.

З рівняння (3): .

З рівняння (1):

З рівняння (2):

З рівняння (6):

З рівняння (4):

З рівняння (5):

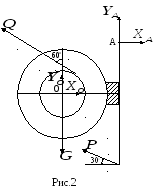
Для перевірки правильності розв’язання задачі складемо рівняння проекцій сил на осі координат для усієї системи (рис.2).

Перевірка (рис.2).

Перевірка виконалась. Задача розв’язана правильно.

Відповідь: P = P_min =1.4 кH; Х_о = 25,3 кН; Х_А = - 6,8 кН;

У_о=- 4кН; У_А = - 4,7кН.

Задача 2.

Визначити максимальне значення сили Р і реакції опор системи, що знаходиться в стані спокою (рис.1). G=3 кн.; a=4 м; b=1 м; α =30о; f =0,4.

Розв’язання.

Розчленуємо систему на окремі тіла: ВС і АС (рис.2). При розчленуванні скористаємося аксіомою взаємодії згідно з якою: , , Реакції жорсткого защемлення в точці А: ХА, YА, МА. Реакції точкової опори в точці В: і . Слід звернути увагу на те, що сили тертя в точках В і С напрямлені в сторони, протилежні напрямкам можливого руху цих точок. Складемо рівняння рівноваги для тіла ВС:

(1)

(2)

(3)

При граничній рівновазі P=P_max, а сили тертя приймають максимальні значення:

(4)

З урахуванням (4) рівняння (1), (2), (3) приймають вид:

(1’)

(2’)

(3’)

З рівняння (2’) . Підстановка в (1’) : , (1’’).

Підстановка (1’’) в (3’):

,

,

, ,

, .

З рівняння (2) , .

З рівняння (1) .

Для перевірки правильності розв’язання задачі складемо рівняння моментів сил відносно точки прикладання сили.

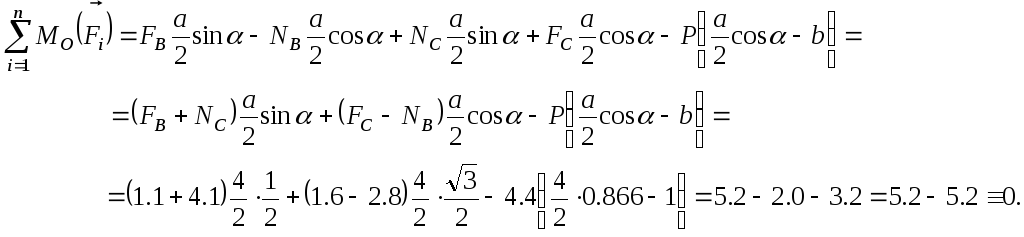
Перевірка виконалась. Задача розв’язана правильно.

Складемо рівняння рівноваги для тіла АС (рис.2).

(1)

(2)

(3)

З рівняння (1): ,

З рівняння (2): ,

З рівняння (3): .

Відповідь: P = P_max =4,4 кH; Х_А=1,6 кН; N_B = 2,8кН; N_C = 4,1 кН;

У_А=4,1 кН; F_B = 1,1 кН; F_c = 1,6 кН;

М_А= 8,2 кНм

Короткі відомості з теорії і методичні вказівки,