Принцип наложения и метод наложения

Принцип наложения для линейных электрических цепей заключается в следующем.

Ток (напряжение ) на любом 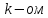участке цепи, в которой одновременно действуют несколько независимых источников электроэнергии, равен алгебраической сумме частичных токов (напряжений ), вызываемых на этом участке каждым из источников в отдельности (- порядковый номер источника, - их количество):

При расчете (определении) токов (и/или напряжений) методом наложения, основанном на сформулированном выше принципе, поступают следующим образом: поочередно находят частичные токи (частичные напряжения ), вызываемые на соответствующих участках цепи каждым из источников в отдельности, после чего, суммируя частичные токи (частичные напряжения) алгебраически, находят действительные токи (напряжения ).

Определение частичных токов (напряжений) в общем случае ведется с использованием частичных схем, в каждой из которых на своем месте оставляется только один, , источник электроэнергии, а все остальные источники исходной схемы заменяются их внутренними сопротивлениями.

При представлении реальных источников электроэнергии схемами замещения, содержащими идеализированные источники электроэнергии - источники ЭДС или источники тока - следует помнить, что внутреннее сопротивление источника ЭДС равно нулю, а внутреннее сопротивление источника тока бесконечно велико, поэтому при замене идеализированных источников ЭДС и тока их внутренними сопротивлениями вместо первых в схему следует включать перемычки (обладающие нулевыми сопротивлениями), а вторые заменять разрывами.

Входные и взаимные проводимости ветвей

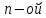Взаимная проводимость между двумя любыми и ветвями линейной электрической цепи по определению равна:

,

где частичный ток в ветви, вызываемый в ней действием только ЭДС источника, входящего в состав ветви (иными словами, при определении проводимости источник в ветви, обладающий ЭДС должен быть единственным в цепи).

По аналогии входная проводимость любой ветви линейной электрической цепи равна:

,

где частичный ток в ветви, вызываемый действием только ЭДС источника, входящего в эту же, ветвь (при условии, что других источников энергии в цепи нет).

Входные и взаимные проводимости ветвей электрической цепи могут быть определены экспериментально или найдены расчетным путем.

Во втором случае удобно применять метод контурных токов. При этом токи в ветвях, входные и взаимные проводимости которых рассчитываются, следует направить по ЭДС ветвей (если такие ЭДС присутствуют в схеме), выбирая независимые контура, каждую из таких ветвей включить только в один контур (первую – в первый, вторую – во второй, третью – в третий и т.д.), приравняв токи в ветвях к соответствующим контурным токам.

Тогда для проводимостей будет верно:

где - главный определитель стандартной системы уравнений метода контурных токов, а – соответствующие алгебраические дополнения.

Рассчитанные по последней формуле взаимные проводимости могут получиться либо положительными, либо отрицательными. Отрицательный знак означает, что ЭДС направленная по контурному току в ветви, вызывает ток в ветви, направленный против выбранного направления контурного тока по ветви.

Проводимости определяются структурой цепи и сопротивлениями ветвей и не зависят от параметров и мест включения источников электроэнергии, так как от этого не зависят определитель и алгебраические дополнения

Передаточные коэффициенты ветвей по напряжению

Передаточный коэффициент по напряжению между и ветвями

,

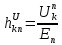где номер ветви, в которую включен единственный для схемы источник электроэнергии с ЭДС , номер ветви, на зажимах которой замеряется напряжение, вызванное действием этого источника.

Передаточные коэффициенты по току

Аналогично определяются передаточные коэффициенты по току между и ветвями:

,

где частичный ток в ветви, вызываемый в ней действием только источника тока , введенного в состав ветви (при определении источник также должен оказаться единственным источником электроэнергии в цепи).

Коэффициенты данного вида в работе не исследуются.

Принцип взаимности

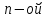В любой линейной электрической цепи ток в ветви, вызванный действием единственной для схемы ЭДС входящей в состав ветви, будет равен току в ветви, вызванному такой же по величине и единственной для схемы ЭДС , включенной в ветвь.

Поэтому для взаимных проводимостей ветвей верно:

.

Линейные соотношения в электрических цепях

Если в линейной электрической цепи изменяется ЭДС или сопротивление в какой-либо одной ветви, то две любые величины (токи и напряжения двух любых ветвей) связаны между собой линейной зависимостью вида:

где роль выполняет ток или напряжение одной ветви, роль - ток или напряжение другой ветви.

Коэффициенты и могут быть найдены как расчетным, так и опытным путем.

При их опытном определении достаточно знать значения двух входящих в уравнение величин (токов, напряжений) при двух различных режимах работы системы и, подставив каждую пару значений в уравнение , решить полученную систему из двух уравнений относительно двух неизвестных .

В данной работе предлагается проверить выполнение линейных соотношений при изменении ЭДС одного из источников электроэнергии.