Лекція 4. Границя функції однієї змінної План

1. Визначення границі функції за Коші і за Гєйне. Геометричний зміст границі функції в точці

2. Границя функції і арифметичні операції

3. Критерій існування границі функції

4. Однобічні границі функції однієї зміної

5. Однобічні границі монотонної функції

1. Визначення границі функції за Коші і за Гєйне. Геометричний зміст границі функції в точці

Нехай функція _{визначена на інтервалі із значеннями в :}

_.

_{Точка .}

_{Визначення 1 (границі функції за Коші). Кажуть, что число} є границею функції _{в точці (чи коли ) і позначають:}

_{, (1)}

_{якщо для таке, що для виконується нерівність:}

_{. (3)}

_{Якщо функція має границю в точці , кажуть, що функція є збіжною в точці чи прямує до} , коли _{. Це можна позначати не тільки в вигляді (1), а і наступним чином:}

_.

Геометричний зміст границі функції полягає у наступному. Якщо в нерівності (3) усунути модуль, вона бути мати вигляд:

_{, (4)}

з якого видно, що _{визначає довільний окіл} : _{, в якому знаходяться всі значення функції , для яких (нерівність (2)), тобто . Інакше кажучи, число} є границею функції _{, коли , якщо для будь-якого -околу числа} знайдеться такий _{-окіл точки} , що для будь-якого аргументу _{функції з цього -околу відповідні значення функції опиняються в -околі (чи в -коридорі) числа} (рис.1).

_{Для поведінки функції в точці можливі два варіанти:}

• Значення _{може співпадати з значенням границі} (рис.2);

• _{функція в точці може бути взагалі не визначеною (рис.3); чи з}начення _{не співпадає з значенням границі} (саме такий випадок зображено на рис.1).

Рис.1.

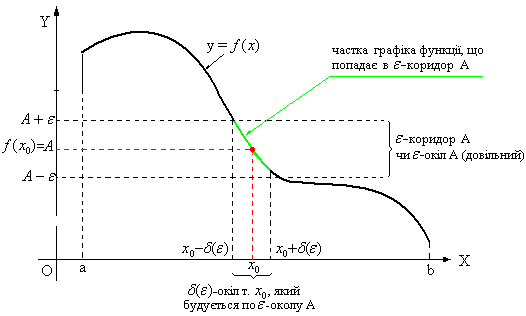
Рис.2.

Рис. 3.

Таким чином, для існування границі функції _{в точці не важлива поведінка функції в самій точці (про це свідчить ліва частина нерівності (2): , яка означає, що розглядаються такі аргументи функції , для яких ). Функція взагалі там може бути невизначеною, а границя буде існувати.}

_{Приклад. Нехай (рис.4). Показати, що для : . Для того, щоб розв’язати поставлену задачу, треба показати, що для (треба отримати формулу, яка виражає через ) таке, що для виконується нерівність:}

_{. (5)}

_{Інакше кажучи, нам треба з нерівності (5) отримати нерівність для оцінки . Для цього розглянемо (5) детально:}

_{. (6)}

_{Якщо ліва частина (6) буде меньшою за , тобто як тільки , то нерівність (5) буде виконуватись автоматично:}

_.

_{Таким чином зрозуміло, що якщо в якості взяти просто , тобто , то для аргументів функції з такого -околу точки буде виконуватися (5). Оскільки - довільне, то задача розв’язана.}

Приклад. _{Нехай . Показати, що .}

_{У цьому випадку . Для того, щоб розв’язати поставлену задачу, треба показати, що для (треба отримати формулу, яка виражає через ) таке, що для виконується нерівність:}

_{. (7)}

_{Інакше кажучи, нерівність (7) треба розв’язати відносно , отримати для оцінку зверху:}

_{. (8)}

_{З (8) витікає, що якщо , тобто , то і (7) буде виконуватися, що й треба було показати.}

_{Визначення 2. Число} не є границею функції _{коли , якщо таке, що для виконується нерівність:}

_.

_{Завдання. З’ясувати, в чому полягає геометричний зміст того, що .}

_{Завдання. Показати, що для функції в точці границі не існує.}

_{Визначення 3 (границі функції за Гєйне). Кажуть, что число} є границею функції _{в точці , якщо для будь-якої послідовності аргументів , для якої виконуються умови:}

_{1) для} ;

2)

_{відповідна послідовність значень функції є збіжною і .}

_{Теорема 1. Визначення 1 і 3 границі функції еквівалентні, тобто якщо за Коші, то і за Гєйне, і навпаки. (без доказу).}

_{Теорема 2. Якщо границя функції в точці існує, то вона єдина. (без доказу).}

_{Наслідок. Нехай для функції побудовані дві послідовності аргументів: і , для яких виконуються умови визначення 3, тобто для} , і _{, . При цьому відповідні послідовності значень функції і такі, що , а , до того . Тоді функція не має границі в точці .}

_{Завдання. Користуючись наслідком з попередньої теореми, довести, що не має границі в точці .}