5. Односторонние пределы монотонной функции

Пусть функция _{определена на .}

_{Определение 8.} Функция _{называется ограниченной сверху на , если , что для выполняется неравенство: . Постоянная называется верхней границей функции на .}

_{Верхних границ у ограниченной сверху функции существует бесконечно много. Наименьшая из всех верхних границ называется точной верхней границей и обозначается: .}

_{Определение 9.} Функция _{называется ограниченной снизу на , если , что для выполняется неравенство: . Постоянная называется нижней границей функции на .}

_{Нижних границ у ограниченной снизу функции существует бесконечно много. Наибольшая из всех нижних границ называется точной нижней границей и обозначается: .}

_{Определение 10.} Функция _{называется ограниченной на , если она ограничена и снизу, и сверху. Иначе:} функция _{является ограниченной на , если , что для выполняется неравенство: .}

_{Пример. Функция является ограниченной, когда , поскольку для : .}

_{Пример. Функция является ограниченной, когда , но не будет ограниченной для .}

_{Определение 11.} Функция _{называется монотонно возрастающей на множестве , если для из того, что следует, что .} Функция _{называется строго монотонно возрастающей на множестве , если для из того, что следует, что .}

_{Определение 12.} Функция _{называется монотонно убывающей на множестве , если для из того, что следует, что .} Функция _{называется строго монотонно убывающей на множестве , если для из того, что следует, что .}

_{Определение 13. Монотонно возрастающие, строго монотонно возрастающие, монотонно убывающие, строго монотонно убывающие функции называются монотонными функциями.}

_{Пример. Функция является строго монотонно возрастающей, когда , строго монотонно убывающей, когда , не является монотонной, когда .}

_{Теорема 6. Пусть функция определена и монотонна на , тогда для в каждой точке существуют оба односторонних предела.}

Вопросы

1. Определения предела функции по Коши, по Гейне.

2. Геометрический смысл предела функции в точке.

3. Как может вообще вести себя функция _{в точке ?}

4. _{Может ли} функция _{в точке иметь предел, если она не определена в этой точке?}

5. _{Как влияет на существование предела функции и значение этого предела в точке поведение функции в самой точке ? Ответ объяснить.}

6. Сколько пределов может иметь функция в точке?

7. Пусть для функци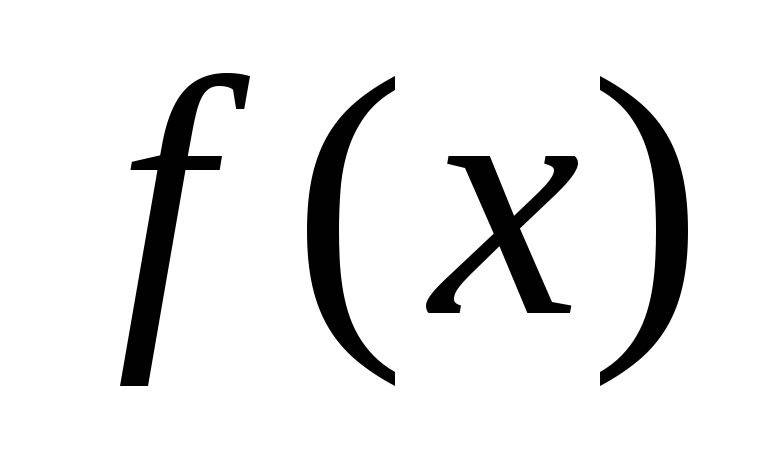й _{и : , . Доказать, что .}

8. Условие Коши для функции _{в точке . Критерий Коши существования предела функции в точке .}

9. Определения односторонних пределов функции в точке _{. Может ли функция не иметь} односторонних пределов в _{точке ? Привести примеры.}

10. Ограниченность функции. Привести примеры ограниченных и неограниченных функций.

11. Монотонность функции. Теорема об односторонних пределах монотонной функции.