
- •Лекция 4. Предел функции одной переменной План
- •1. Определение предела функции по Коши и по Гейне. Геометрический смысл предела функции в точке
- •2. Предел функции и арифметические операции
- •3. Критерий существования предела функции
- •4. Односторонние пределы функции одной переменной
- •5. Односторонние пределы монотонной функции
- •Вопросы
Лекция 4. Предел функции одной переменной План
-
Определение предела функции по Коши и по Гейне. Геометрический смысл предела функции в точке
-
Предел функции и арифметические операции
-
Критерий существования предела функции
-
Односторонние пределы функции одной переменной
-
Односторонние пределы монотонной функции
1. Определение предела функции по Коши и по Гейне. Геометрический смысл предела функции в точке
Пусть функция
![]() определена на интервале
определена на интервале
![]() со значениями в
со значениями в
![]() :
:
![]() .
.
Точка
![]() .
.
Определение 1 (предела
функции по Коши).
Говорят, что число
![]() является пределом функции
является пределом функции
![]() в
точке
в
точке
![]() (когда
(когда
![]() ) и обозначают:
) и обозначают:
![]() ,
(1)
,
(1)
если для
![]() такое, что для
такое, что для
![]() имеет место неравенство:
имеет место неравенство:
![]() .
(3)
.
(3)
Если функция имеет предел
в точке
![]() ,
говорят, что функция является сходящейся
в точке
,
говорят, что функция является сходящейся
в точке
![]() или стремится к
или стремится к
![]() ,
когда
,
когда
![]() .
Это можно обозначать не только в виде
(1), а и следующим образом:
.
Это можно обозначать не только в виде
(1), а и следующим образом:
![]() .
.
Геометрический смысл предела функции состоит в следующем. Если в неравенстве (3) убрать модуль, оно будет иметь вид:
![]() ,
(4)
,
(4)
откуда видно, что
![]() определяет произвольную окрестность
определяет произвольную окрестность
![]() :
:
![]() ,
в которой находятся все значения функции
,
в которой находятся все значения функции
![]() ,
для которых
,
для которых
![]() (неравенство (2)), т.е.
(неравенство (2)), т.е.
![]() .
Иначе говоря, число
.
Иначе говоря, число
![]() является пределом функции
является пределом функции
![]() ,
когда
,
когда
![]() ,
если для любой
,
если для любой
![]() -окрестности
числа
-окрестности
числа
![]() найдется такая
найдется такая
![]() -окрестность
точки
-окрестность
точки
![]() ,
что для любого аргумента
,
что для любого аргумента
![]() функции
функции
![]() из этой
из этой
![]() -окрестности
соответствующие значения функции
оказываются в
-окрестности
соответствующие значения функции
оказываются в
![]() -окрестности
(или в
-окрестности
(или в
![]() -коридоре)
числа
-коридоре)
числа
![]() (рис.1).
(рис.1).
Для поведения функции
![]() в точке
в точке
![]() возможны два варианта:
возможны два варианта:
-
Значение
 может совпадать со значением предела
может совпадать со значением предела
 (рис.2);
(рис.2); -
функция
 в точке
в точке
 может быть вообще неопределенной
(рис.3); или значение
может быть вообще неопределенной
(рис.3); или значение
 не совпадает со значением предела
не совпадает со значением предела
 (именно такой случай изображен на
рис.1).
(именно такой случай изображен на
рис.1).
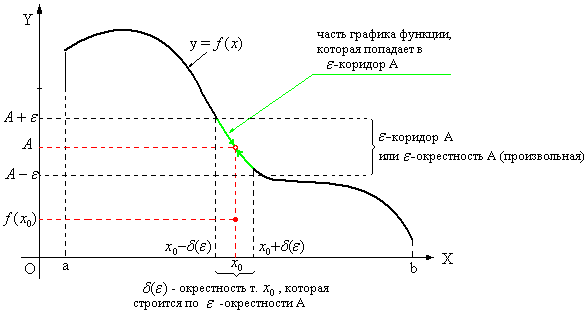
Рис.1.

Рис.2.

Рис. 3.
Таким образом, для существования
предела функции
![]() в точке
в точке
![]() не
важно поведение функции в самой точке
не
важно поведение функции в самой точке
![]() (об этом свидетельствует левая часть
неравенства (2):
(об этом свидетельствует левая часть
неравенства (2):
![]() ,
которая означает, что рассматриваются
такие аргументы
,
которая означает, что рассматриваются
такие аргументы
![]() функции
функции
![]() ,
для которых
,
для которых
![]() ).
Функция вообще там может быть
неопределенной, а предел будет
существовать.
).
Функция вообще там может быть
неопределенной, а предел будет
существовать.
П ример.
Пусть
ример.
Пусть
![]() (рис.4). Показать, что для
(рис.4). Показать, что для
![]() :
:
![]() .
Для того, чтобы решить поставленную
задачу, надо показать, что для
.
Для того, чтобы решить поставленную
задачу, надо показать, что для
![]() (надо получить формулу, которая выражает
(надо получить формулу, которая выражает
![]() через
через
![]() )
такое, что для
)
такое, что для
![]() выполняется неравенство:
выполняется неравенство:
![]() .
(5)
.
(5)
Иначе говоря, нам надо из
неравенства (5) получить неравенство
для оценки
![]() .
Для этого рассмотрим (5) детально:
.
Для этого рассмотрим (5) детально:
 .
(6)
.
(6)
Если левая часть (6) будет
менше
![]() ,
т.е. как только
,
т.е. как только
![]() ,
то неравенство (5) будет выполняться
автоматически:
,
то неравенство (5) будет выполняться
автоматически:
![]() .
.
Таким образом понятно, что
если в качестве
![]() взять просто
взять просто
![]() ,
т.е.
,
т.е.
![]() ,
то для аргументов функции
,
то для аргументов функции
![]() из этой
из этой
![]() -окрестности
точки
-окрестности
точки
![]() будет выполняться (5). Поскольку
будет выполняться (5). Поскольку
![]() - произвольное, то задача решена.
- произвольное, то задача решена.
Пример.
Пусть
![]() .
Показать, что
.
Показать, что
![]() .
.
В этом случае
![]() .
Для того, чтобы решить поставленную
задачу, надо показать, что для
.
Для того, чтобы решить поставленную
задачу, надо показать, что для
![]() (надо получить формулу, которая выражает
(надо получить формулу, которая выражает
![]() через
через
![]() )
такое, что для
)
такое, что для
![]() выполняется неравенство:
выполняется неравенство:
![]() .
(7)
.
(7)
Иначе говоря, неравенство
(7) надо решить относительно
![]() ,
получить для
,
получить для
![]() оценку сверху:
оценку сверху:
 .
(8)
.
(8)
Из
(8) следует, что если
![]() ,
т.е.
,
т.е.
![]() ,
то и (7) будет выполняться.
,
то и (7) будет выполняться.
Определение 2.
Число
![]() не является
пределом функции
не является
пределом функции
![]() ,
когда
,
когда
![]() ,
если
,
если
![]() такое, что для
такое, что для
![]()
![]() выполняется неравенство:
выполняется неравенство:
![]() .
.
Задание.
Выяснить, в чем состоит геометрический
смысл того, что
![]() .
.
Задание.
Показать, что для функции
 в точке
в точке
![]() предела не существует.
предела не существует.
Определение 3 (предела
функции по Гейне).
Говорят, что число
![]() является пределом функции
является пределом функции
![]() в точке
в точке
![]() ,
если для любой последовательности
аргументов
,
если для любой последовательности
аргументов
![]() ,
для которой выполняются условия:
,
для которой выполняются условия:
1)
![]() для
для
![]() ;
;
2)
![]()
соответствующая
последовательность значений функции
![]() является сходящейся и
является сходящейся и
![]() .
.
Теорема 1.
Определения 1 и 3 предела функции
эквивалентны, т.е. если
![]() по Коши, то
по Коши, то
![]() и по Гейне, и наоборот. (без доказательства).
и по Гейне, и наоборот. (без доказательства).
Теорема 2.
Если предел функции
![]() в точке
в точке
![]() существует,
то он единственный. (без доказательства).
существует,
то он единственный. (без доказательства).
Следствие.
Пусть для функции
![]() построены две последовательности
аргументов:
построены две последовательности
аргументов:
![]() и
и
![]() ,
для которых выполняются условия
определения 3, те.е.
,
для которых выполняются условия
определения 3, те.е.
![]() для
для
![]() ,
и
,
и
![]() ,
,
![]() .
При этом соответствующие последовательности
значений функции
.
При этом соответствующие последовательности
значений функции
![]() і
і
![]() такие, что
такие, что
![]() ,
а
,
а
![]() ,
и
,
и
![]() .
Тогда функция
.
Тогда функция
![]() не
имеет предела в точке
не
имеет предела в точке
![]() .
.
Задание.
Пользуясь следствием из предыдущей
теоремы, доказать, что
![]() не имеет предела в точке
не имеет предела в точке
![]() .
.
