
- •Распределения функций от случайных величин 1
- •Дискретная св имеет ряд распределения
- •Многомерные cв
- •Плотность распределения вероятностей случайного вектора (X,y) имеет вид . Найти константу с и вычислить .
- •В условиях предыдущей задачи найти безусловные плотности распределения cв X и y. Установить, зависимы или нет эти cв.
- •Распределения функций от случайных величин 2
- •Числовые характеристики cв
- •Производящая функция cв
Числовые характеристики cв
-
Найти МО и дисперсию CВ, распределенной равномерно на отрезке
 .
. -
Найти МО и дисперсию CВ, распределенной по показательному закону с параметром
 .
. -
Найти МО и дисперсию CВ, распределенной по закону Пуассона с параметром
 .
. -
Найти МО и дисперсию CВ
 ,
распределенной по закону Паскаля с
плотностью
,
распределенной по закону Паскаля с
плотностью
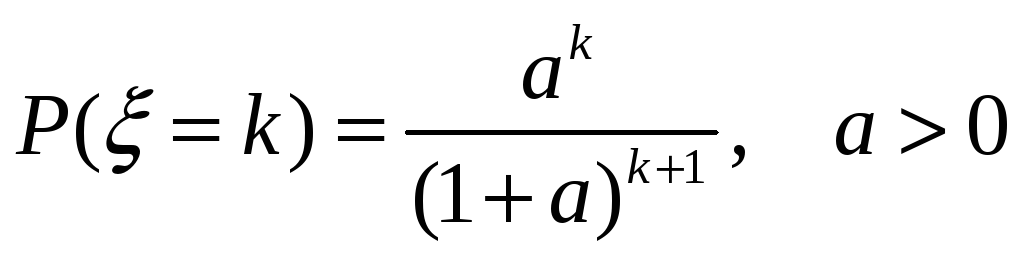 .
. -
Найти МО и дисперсию CВ, распределенной по биномиальному закону с параметрами
 .
. -
Найти МО и дисперсию CВ, распределенной по нормальному закону с параметрами
 .
. -
CВ
 распределена равномерно на отрезке
распределена равномерно на отрезке
 .
Найти МО и дисперсию CВ
.
Найти МО и дисперсию CВ
 .
Являются ли CВ
.
Являются ли CВ
 и
и
 независимыми?
независимыми? -
Найти МО и дисперсию CВ
 с распределением
с распределением
 .
. -
Найти МО CВ
 ,
если CВ
,
если CВ
 распределена по нормальному закону с
параметрами
распределена по нормальному закону с
параметрами
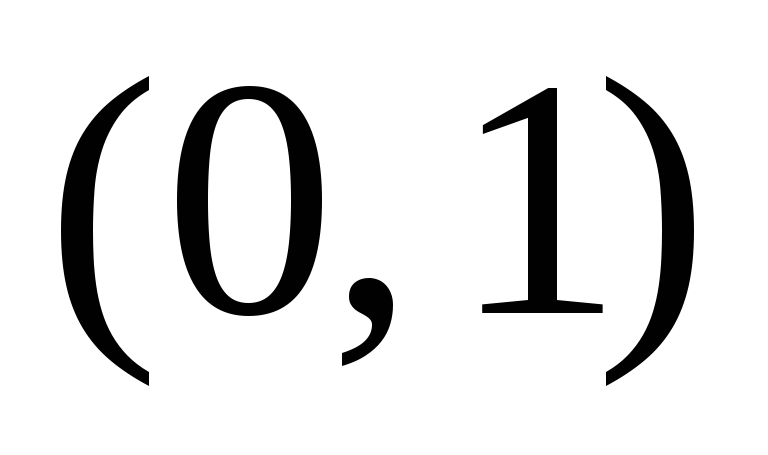 .
. -
Найти МО и дисперсию CВ
 ,
если CВ
,
если CВ
 распределена по биномиальному закону
с параметрами
распределена по биномиальному закону
с параметрами
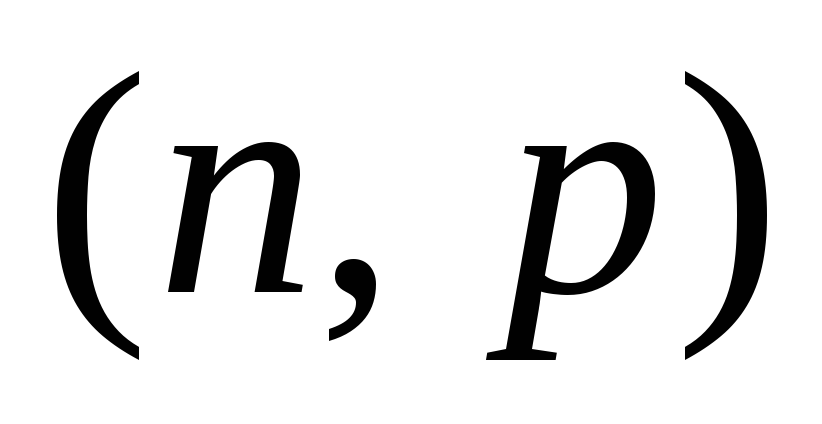 .
. -
Найти МО CВ
 ,
если CВ
,
если CВ
 распределена по закону Пуассона с
параметром
распределена по закону Пуассона с
параметром
 .
. -
Найти МО CВ
 ,
если CВ
,
если CВ
 распределена по биномиальному закону
с параметрами
распределена по биномиальному закону
с параметрами
 .
. -
Найти МО и дисперсию а) числа очков, выпадающих при бросании одной игральной кости: б) суммы очков, выпадающих при бросании n игральных костей.
-
В урне находится 10 шаров, из них 3 черных. Наугад вынимается 2 шара. Найти среднее число вынутых черных шаров.
-
Из урны, содержащей 5 белых и 3 черных шара, извлекли 2 шара и положили в урну, содержащую 2 белых и 1 черный шар. Найти среднее число черных шаров во второй урне.
-
Стрелок стреляет в цель до тех пор, пока не поразит ее. Вероятность попадания при отдельном выстреле равна
 .
Найти МО и дисперсию
числа
произведенных выстрелов.
.
Найти МО и дисперсию
числа
произведенных выстрелов. -
CВ
 может принимать только значения -2, -1,
0, 1, 2. С какими вероятностями
может принимать только значения -2, -1,
0, 1, 2. С какими вероятностями
 принимает эти значения, если
принимает эти значения, если
 .
. -
На отрезок (0, L) наудачу брошены 2 точки. Найти среднее расстояние между ними.
-
Точка брошена наудачу внутрь круга радиуса R. Найти среднее расстояние от точки до центра круга.
-
Мишень состоит из трех концентрических кругов радиусом
 ,
1 и
,
1 и
 .
Попадание в центральный круг стоит 4
очка, в среднее кольцо – 3 очка, в крайнее
кольцо 2 очка. Вероятность попадания
на расстоянии
.
Попадание в центральный круг стоит 4
очка, в среднее кольцо – 3 очка, в крайнее
кольцо 2 очка. Вероятность попадания
на расстоянии
 от центра мишени равна
от центра мишени равна
 .
Найти среднее число очков, выбитых при
5 выстрелах.
.
Найти среднее число очков, выбитых при
5 выстрелах. -
На окружность радиуса R наудачу ставятся 2 точки, которые затем соединяются между собой и центром окружности. Найти среднее значение площади полученного треугольника.
-
CВ
 и
и
 независимы и имеют плотности
независимы и имеют плотности
 и
и
 соответственно.
Найти МО CВ
соответственно.
Найти МО CВ
 .
. -
Найти МО CВ
 ,
если CВ
,
если CВ
 распределена по закону Коши с плотностью
распределена по закону Коши с плотностью .
. -
CВ
 и
и
 независимы и имеют следующие числовые
характеристики:
независимы и имеют следующие числовые
характеристики:
 .
Найти МО следующих CВ
.
Найти МО следующих CВ
 .
. -
Совместная плотность вероятностей CВ
 и
и
 равна
равна
 ,
где G
– треугольник, ограниченный прямыми
,
где G
– треугольник, ограниченный прямыми
 .
Найти а) константу
.
Найти а) константу
 ,
б)
,
б)
 ,
в)
,
в)

-
CВ
 и
и
 имеют следующие числовые характеристики:
имеют следующие числовые характеристики:
 и коэффициент корреляции
и коэффициент корреляции
 .
Найти МО и дисперсию CВ
.
Найти МО и дисперсию CВ
 .
. -
Найти коэффициент корреляции между CВ
 и
и
 ,
если
,
если
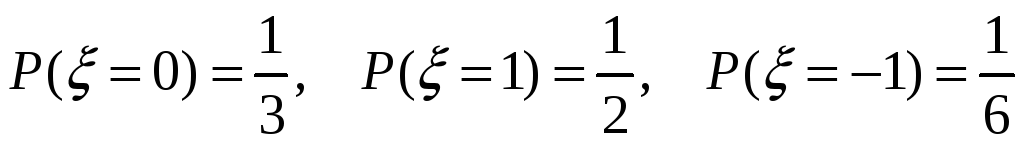 .
. -
Найти коэффициент корреляции между CВ
 и
и
 ,
если
,
если
 имеет стандартное нормальное
распределение.
имеет стандартное нормальное
распределение. -
CВ
 и
и
 независимы, причем
независимы, причем
 ,
,
 .
Будут ли CВ
.
Будут ли CВ
 и
и
 а) независимыми, б) некоррелированными?
а) независимыми, б) некоррелированными? -
