
- •Распределения функций от случайных величин 1
- •Дискретная св имеет ряд распределения
- •Многомерные cв
- •Плотность распределения вероятностей случайного вектора (X,y) имеет вид . Найти константу с и вычислить .
- •В условиях предыдущей задачи найти безусловные плотности распределения cв X и y. Установить, зависимы или нет эти cв.
- •Распределения функций от случайных величин 2
- •Числовые характеристики cв
- •Производящая функция cв
Распределения функций от случайных величин 1
1.
СВ
![]() имеет плотность
имеет плотность
![]() .
Найти плотности случайных величин 1)
.
Найти плотности случайных величин 1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
-
CВ
 имеет плотность
имеет плотность
 .
Найти плотности следующих CВ
1)
.
Найти плотности следующих CВ
1)
 ,
2)
,
2)
 ,
3)
,
3)
 ,
4)
,
4)
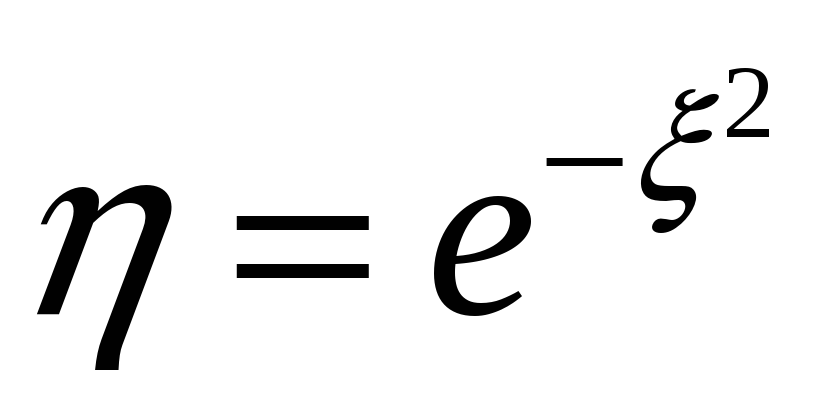 ,
5)
,
5)
 .
. -
CВ
 имеет непрерывную функцию распределения
имеет непрерывную функцию распределения
 .
Найти функцию распределения CВ
.
Найти функцию распределения CВ
 .
. -
СВ
 распределена по закону
распределена по закону
 .
Найти функцию распределения CВ
.
Найти функцию распределения CВ
 .
. -
Диаметр круга измерен приближенно. Считая, что его величина равномерно распределена на отрезке
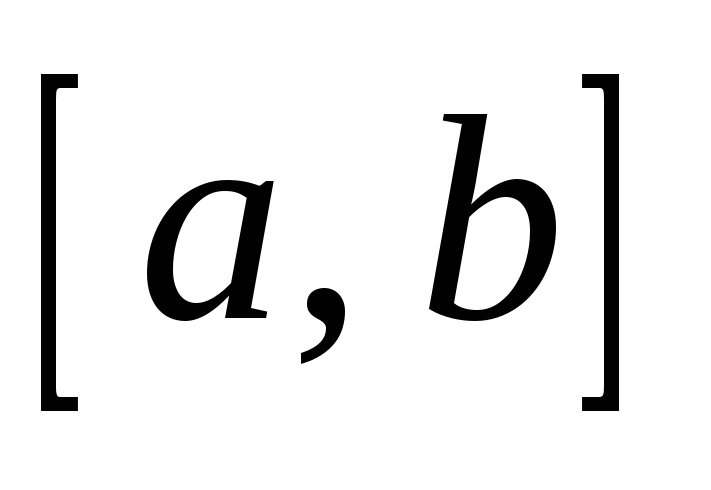 ,
найти плотность распределения площади
круга.
,
найти плотность распределения площади
круга. -
На отрезок оси ординат между точками (0,0) и (0, R) наудачу брошена точка (то есть ее ордината равномерно распределена в промежутке (0, R)). Через точку попадания проведена хорда окружности
 ,
перпендикулярная оси 0y.
Найти распределение длины этой хорды.
,
перпендикулярная оси 0y.
Найти распределение длины этой хорды. -
Стержень длины L разламывается в наудачу выбранной точке. Вероятность того, что точка разлома попадет на какую-либо часть стержня, пропорциональна длине этой части. Найти функцию распределения площади прямоугольника, стороны которого равны получившимся кускам стержня.
-
Острый угол ромба со стороной L подчинен закону равномерного распределения на отрезке
 Найти плотность вероятностей площади
ромба.
Найти плотность вероятностей площади
ромба. -
СВ
 распределена по нормальному закону с
плотностью
распределена по нормальному закону с
плотностью
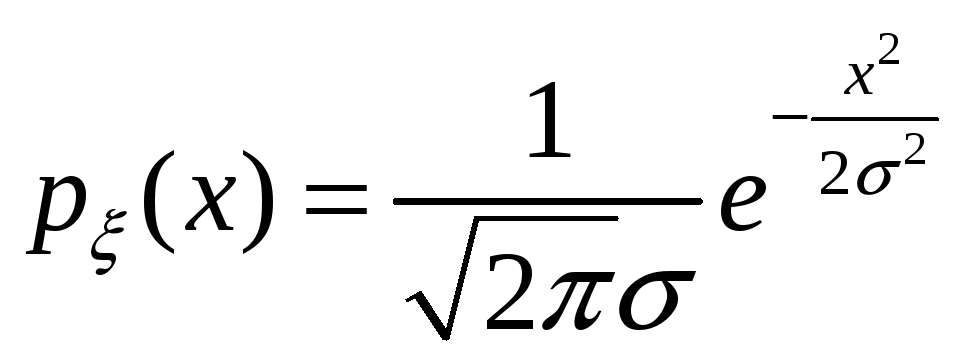 .
Найти закон распределения величины
.
Найти закон распределения величины
 .
. -
СВ
 распределена по показательному закону
с плотностью
распределена по показательному закону
с плотностью
 Найти функцию распределения и плотность
вероятностей CВ
Найти функцию распределения и плотность
вероятностей CВ
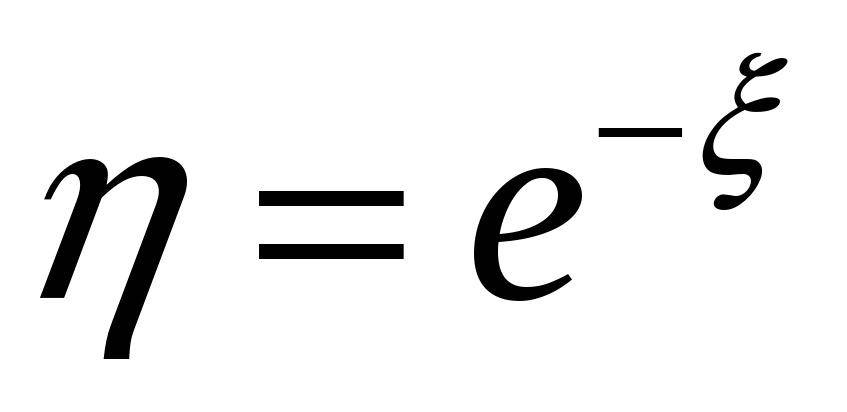 .
. -
СВ
 распределена по показательному закону
с параметром
распределена по показательному закону
с параметром
 .
Найти плотности вероятностей CВ
.
Найти плотности вероятностей CВ
 .
. -
СВ
 распределена равномерно в интервале
распределена равномерно в интервале
 Найти закон распределения величины
Найти закон распределения величины

-
СВ
 распределена равномерно в интервале
(0, 1). Найти плотность вероятностей СВ
распределена равномерно в интервале
(0, 1). Найти плотность вероятностей СВ

-
СВ
 распределена равномерно в интервале
(-1,2). Найти плотность вероятностей CВ
распределена равномерно в интервале
(-1,2). Найти плотность вероятностей CВ

-
СВ
 распределена по закону Коши с плотностью
распределена по закону Коши с плотностью
 .
Найти плотности вероятностей CВ
.
Найти плотности вероятностей CВ
 .
. -
СВ
 имеет ФР
имеет ФР
 .
Найти ФР следующих СВ
.
Найти ФР следующих СВ

-
Дискретная СВ
 имеет ряд распределения
имеет ряд распределения
-

-2
-1
0
1
2
P
0,1
0,2
0,3
0,3
0,1
Найти ряды распределения
следующих CВ
1)
![]() ,
2)
,
2)
![]()
-
Дискретная св имеет ряд распределения
-




P
0,2
0,7
0,1
Найти ряд
распределения
CВ
![]()
Многомерные cв
