Тема 6: -функция Дирака.

Определения и глоссарий

Обобщенные функции, производная разрывной функции

Задания для предварительной самостоятельной подготовки

1. Уяснить основное свойство -функции как фильтра, ставящего в соответствие функции ее значения в некоторых точках.

2. Привести примеры использования -функции для задания плотностей физических величин, сосредоточенных в дискретных точках пространства.

Задачи

1. Вычислить интегралы

a) е)

б) ж)

в) з)

г) и)

д) к)

2. Найти преобразование Фурье и Лапласа от 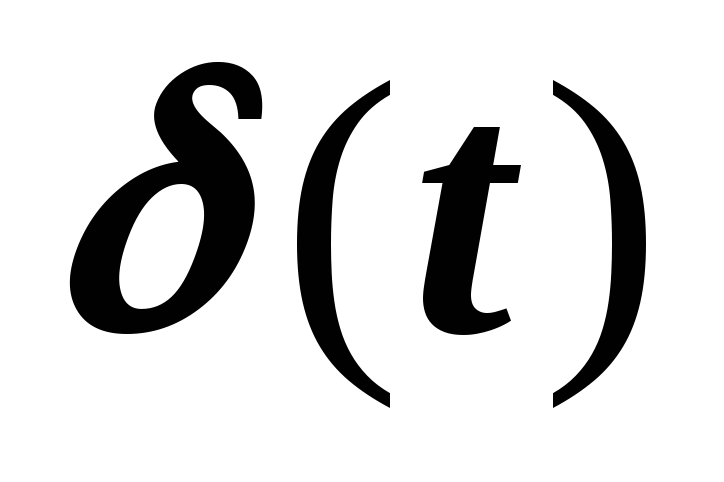. Обсудить полученный результат.

3. Показать, что

а) б)

в) г)

д)

4. Разложением в ряд Фурье доказать соотношение

5. Используя символическое равенство 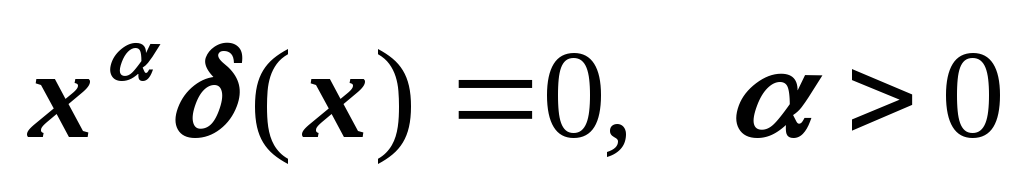, найти общее решение уравнения 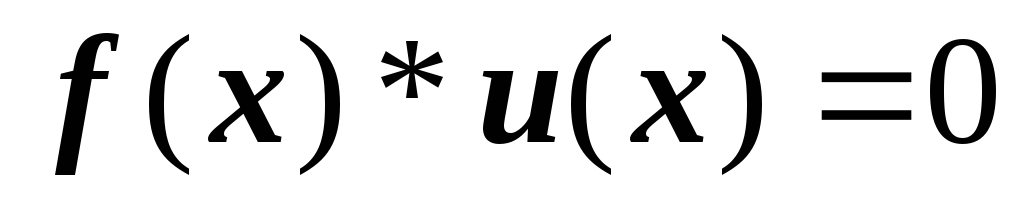относительно неизвестной функции .

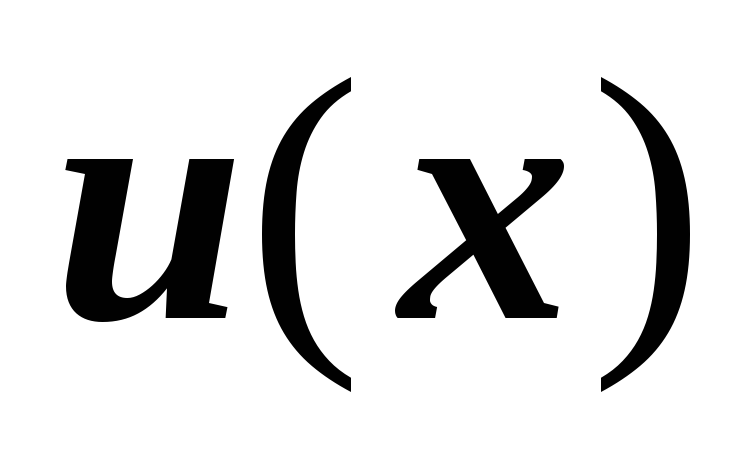6. Закон дисперсии и поляризационный вектор 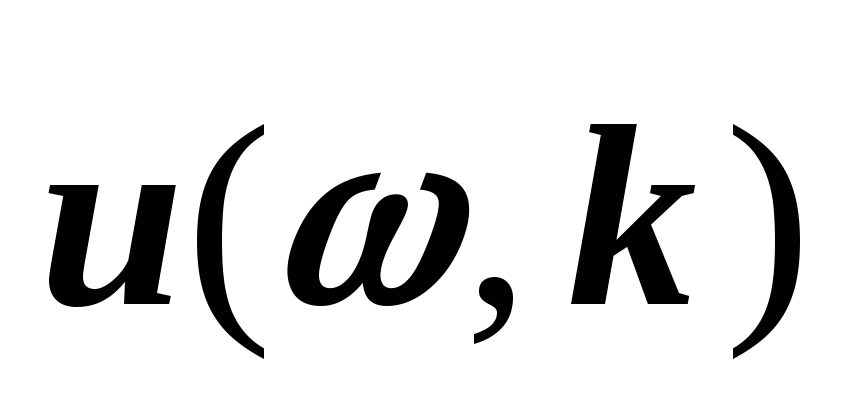волн различной природы, способных распространяться с угловой частотой и волновым вектором по среде передачи информации, часто получается как решение уравнения вида . Решить это уравнение, используя свойства -функции, и проинтерпретировать результат.

7. Вычислить производную функции распределения равномерно распределенной в интервале [1,5] целочисленной случайной величины.

8. Записать общее выражение для производной функции .

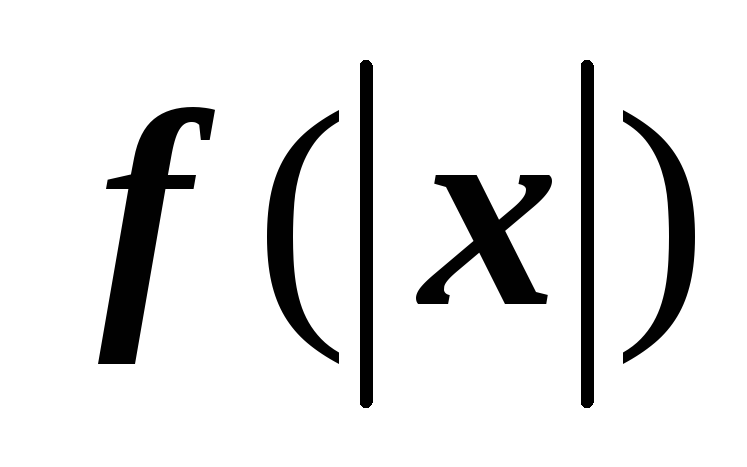Учебно-исследовательское задание

1. Законы дисперсии и собственные возбуждения сред передачи информации .

Литература

1. В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.

2. В.М.Рабинович. Введение в теорию колебаний и волн. М.:Наука, 1989.

Практическое занятие 9.

Тема 7: Преобразования одномерных случайных величин.

Определения и глоссарий

Детерминированная функция как преобразование

Задания для предварительной самостоятельной подготовки

1. Повторить таблицу неопределенных интегралов из курса высшей математики.

Задачи

1. Дискретная случайная величина Х характеризуется распределением

xi	-2	-1	0	1	2
pi	0,1	0,2	0,3	0,3	0,1

Найти законы распределения случайных величинY=Х²+1, Z=|X|.

2. Случайная величина Y является линейной функцией случайной величины Х: Y = аХ +b, где а и b - постоянные величины. Найти плотность вероятности р₁(y) величины Y при известной плотности вероятности р₁(х) случайной величины Х.

3. Равномерно распределенная в интервале [-2,3] случайная величина Х подвергается квадратичному преобразованию Y=X². Определить и построить функцию распределения и плотность распределения случайной величины Y.

4. Случайная величина Х описывается биноминальным законом распределения вероятностей. Найти математическое ожидание m_у и дисперсию ²_у случайной величины Y = е^аХ .

5. Случайная величина Х подчинена равномерному закону в интервале от 0 до 2. Определить математическое ожидание и дисперсию величины Y = 6Х².

6. Случайная величина Х с плотностью вероятности 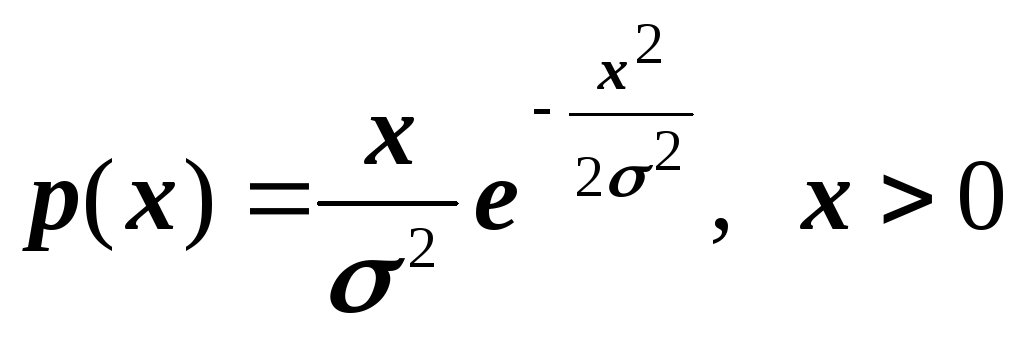, подвергается преобразованию 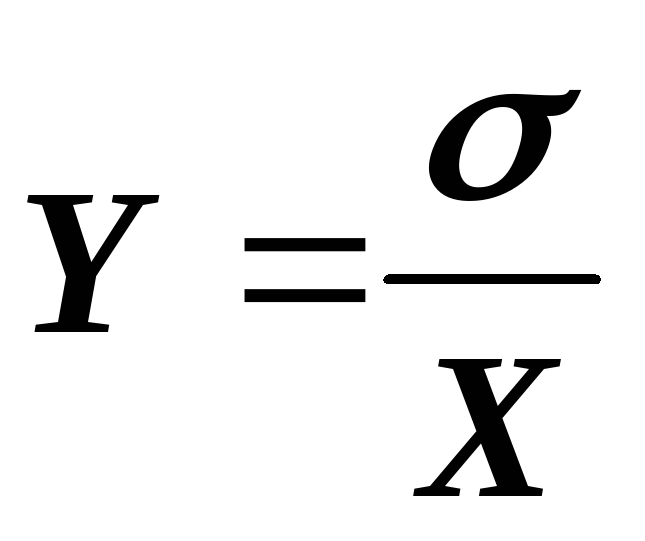. Найти плотность распределения Y.

7. Нормально распределенная случайная величина Х подвергается квадратичному преобразованию Y=X². Определить плотность распределения случайной величины Y. Как изменится результат, если Х имеет ненулевое математическое ожидание?

8. Случайная величина Х с плотностью вероятности , подвергается преобразованию 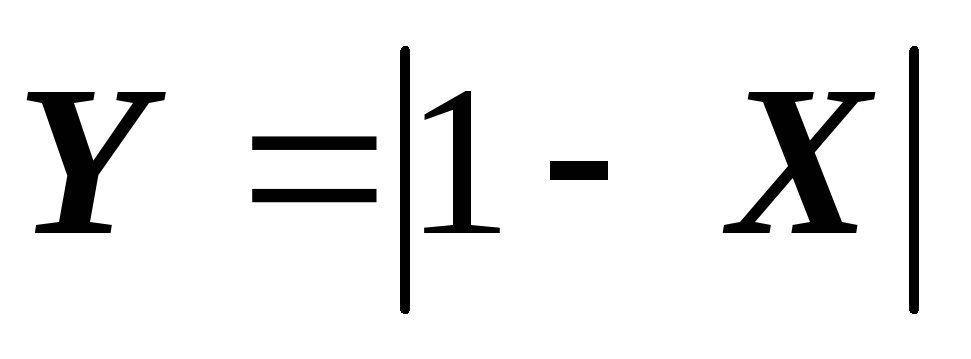. Найти плотность распределения Y.

9. Найти плотность распределения, математическое ожидание и дисперсию гармонического случайного сигнала с постоянными амплитудой и частотой, начальная фаза которого равномерно распределена в интервале .

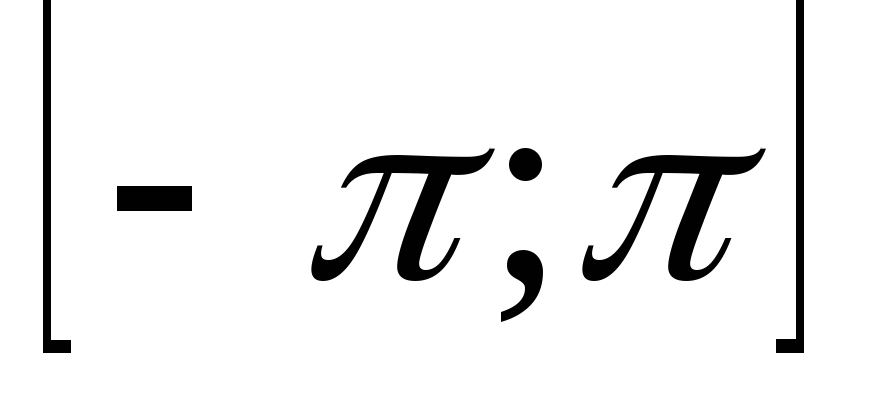10. Случайный сигнал задан в виде 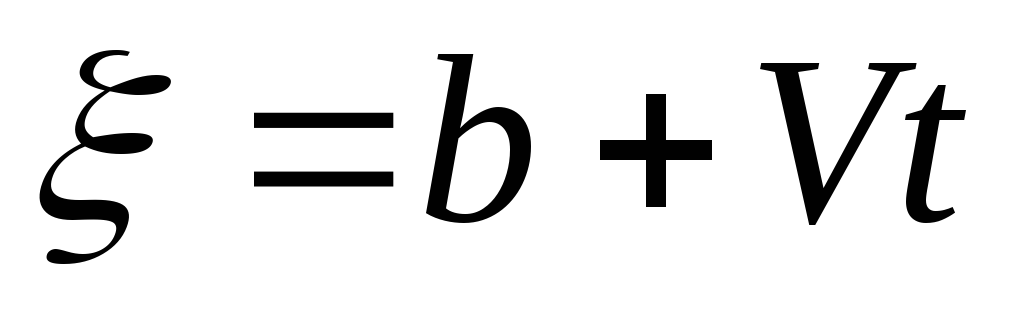, где b - известная постоянная, V -случайная величина, распределенная по нормальному закону с математическим ожиданием 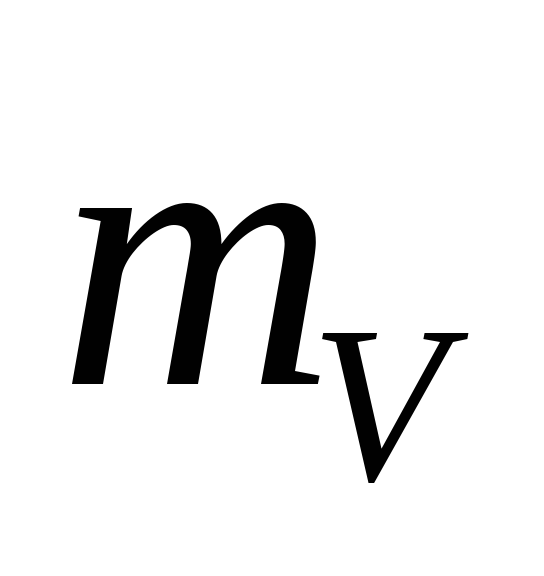и дисперсией 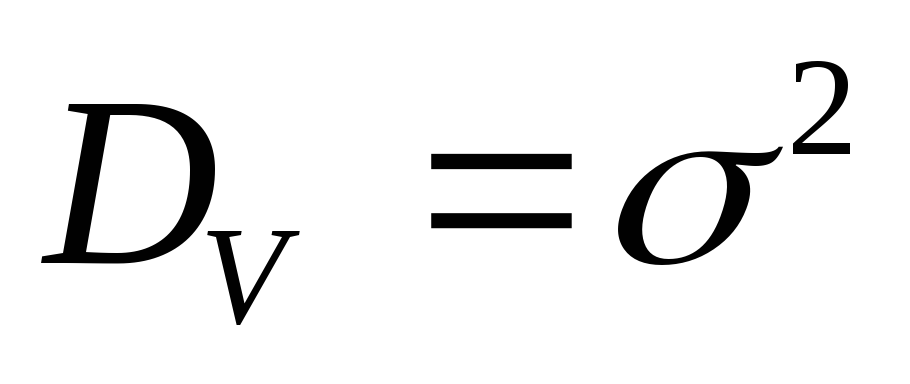. Найти плотность сигнала , его математическое ожидание 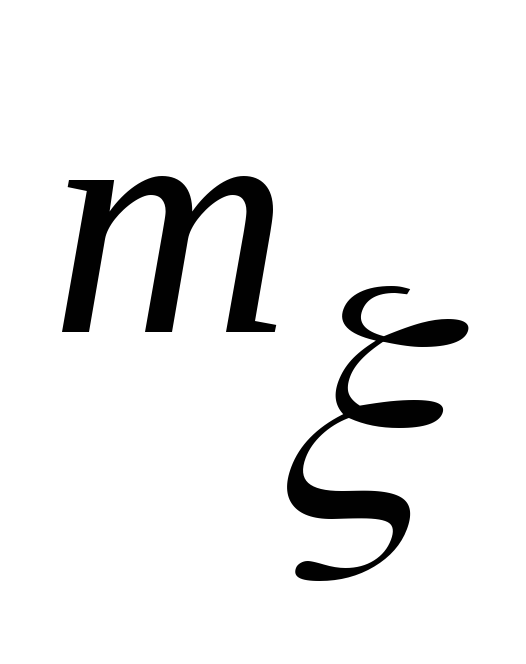и дисперсию .

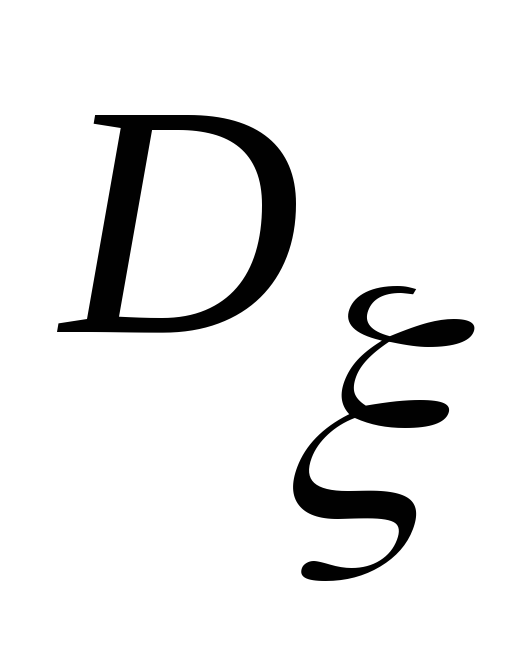Учебно-исследовательское задание

1. Произвести вывод распределения молекул идеального газа по скоростям (распределение Максвелла) из условия максимума информационной энтропии при заданной средней кинетической энергии системы, равной 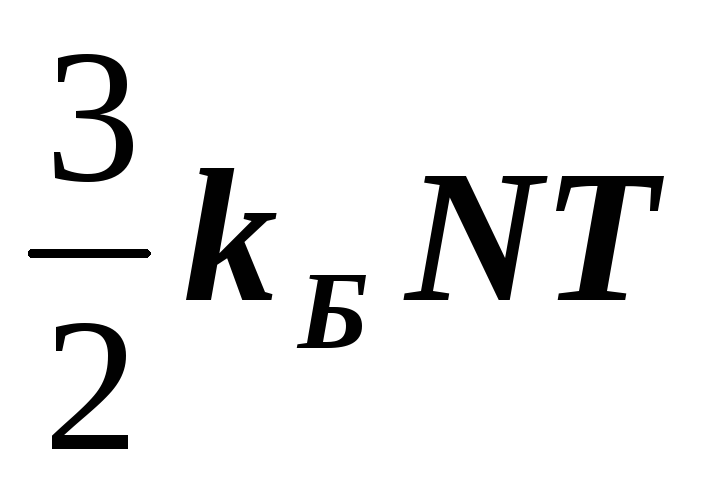, где N – число молекул, T- температура. Получить из этого распределения распределение молекул по энергиям [3].

Литература

1. В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.

2. В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.

3. И.В.Савельев. Курс общей физики, Т.2. М: Высшая школа, 1987.

Практическое занятие 10.