Тема 1: Информация и ее измерение. Определения и глоссарий

Система – совокупность взаимодействующих элементов.

Подсистема – элемент системы.

Надсистема данной системы – система, подсистемой которой является данная система.

Окружение системы – совокупность систем, элементами которых являются надсистемы данной системы (объемлющая система).

Информация о системе – образ системы в ее окружении, совокупность надсистем данной системы. Полная информация о системе – воспроизведение самой системы.

Количество информации – мера неопределенности состояния наблюдателя, снятой испытанием системы.

Количество информации по Харди – максимальное количество вопросов, которое необходимо задать, чтобы любой из элементов множества мощностью N мог быть однозначно определен: .

Неожиданность элемента множества – мера информационной значимости появления конкретного элемента множества при случайном выборе из дискретного множества с распределением вероятностей , i =1,…,N,

Среднее значение признака G на множестве Х – .

Количество информации по Шеннону – средняя неожиданность на Х, .

Информационная энтропия системы – мера неопределенности задания состояний элементов системы при заданном состоянии системы. Характеризует состояние системы и определяется по Больцману как , где - постоянная Больцмана, W –количество состояний элементов системы, совместимых с данным состоянием всей системы. Применяется в статистическом обосновании равновесной термодинамики. В случае систем, составленных из большого числа М одинаковых элементов, каждый из которых может находится в одном из N состояний с вероятностью , с точностью до множителя совпадает с количеством информации по Шеннону: .

Задания для предварительной самостоятельной подготовки

1. Сформулировать понятие ценности информации и привести примеры систем, в которых информация характеризуется ценностью.

2. Определить соотношение понятий информации о системе и модели системы.

3. Привести примеры систем, неопределенность которых не может быть полностью снята каким-либо испытанием.

Задачи

1. Доказать, что в случае равнораспределения вероятности по элементам множества количество информации по Щеннону сводится к количеству информации по Харди.

2. Предложить алгоритм задания вопросов, реализующий количество информации по Харди для множества студентов группы.

3. Какое количество информации получает школьник младших классов при работе в научной лаборатории в течении 10 минут, если ему поручено записывать показания восьмиразрядного цифрового вольтметра с интервалом в 10 секунд.

4. Как изменится количество информации, получаемой при некотором измерении, если используемый измерительный прибор заменить на более точный с ценой деления шкалы, в 100 раз меньшей цены деления исходной.

5. В партии 100 сенсоров, из них 5% бракованных. Из партии выбирают наугад 5 сенсоров для контроля. Какое количество информации содержится в сообщении о том, что в случайной выборке оказалось ровно 3 бракованных прибора?

6. Многоканальная сенсорная система состоит из 32 равнонадежных элементов и имеет устройство контроля их исправности. Определить минимальное число проб, которое необходимо выполнить этому устройству, чтобы установить любой неисправный элемент.

7. Для случая, когда в каждом испытании некоторой системы реализуется один из двух возможных исходов с заданной вероятностью p, записать количество получаемой в таком испытании информации по Шеннону 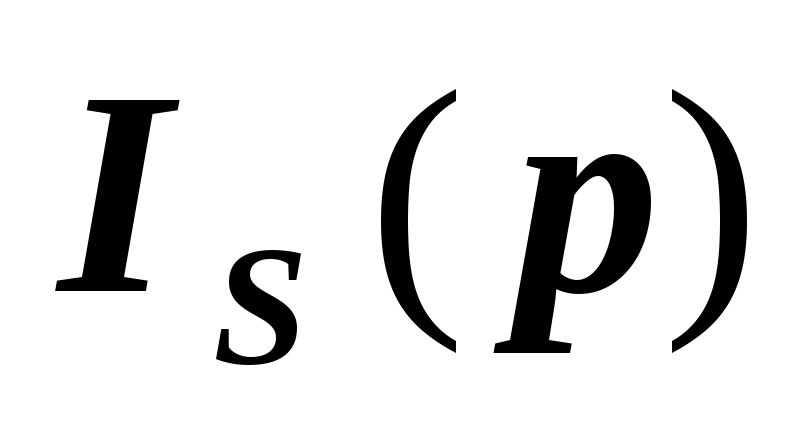и найти максимум этой функции. Построить график функции 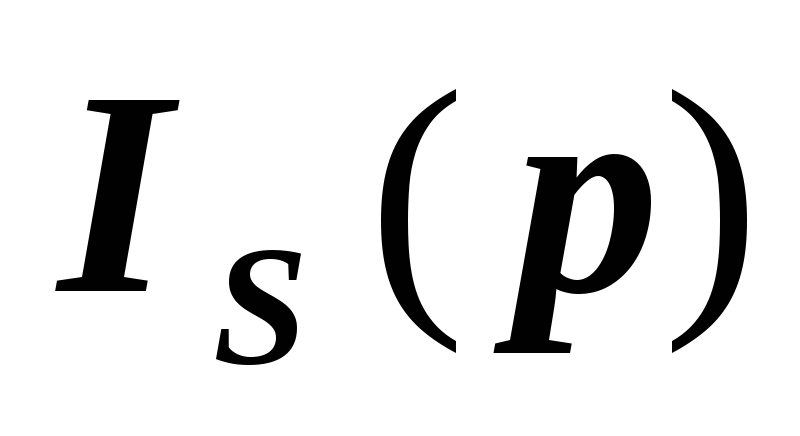и проинтерпретировать полученный результат.

8. Используя метод неопределенных множителей Лагранжа, показать, что для системы, которая может находиться в одном из N состояний с вероятностью 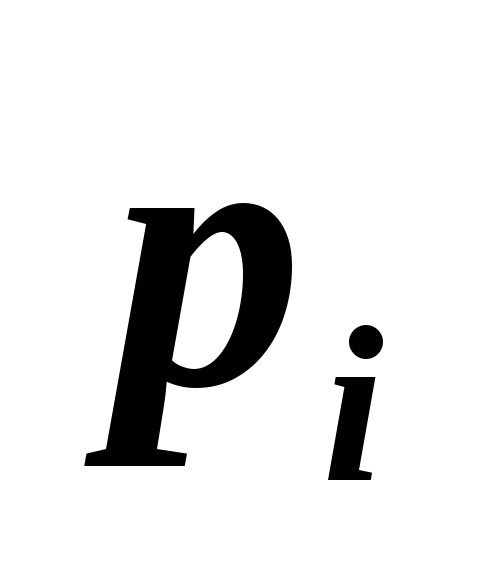, где 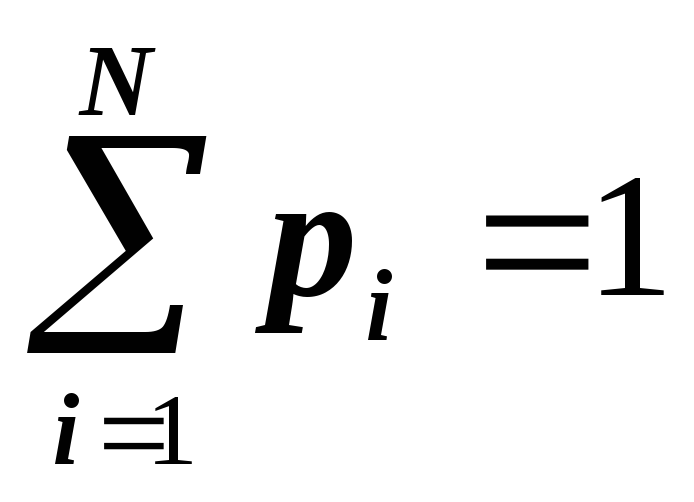, максимуму информационной энтропии соответствует равномерное распределение вероятностей .

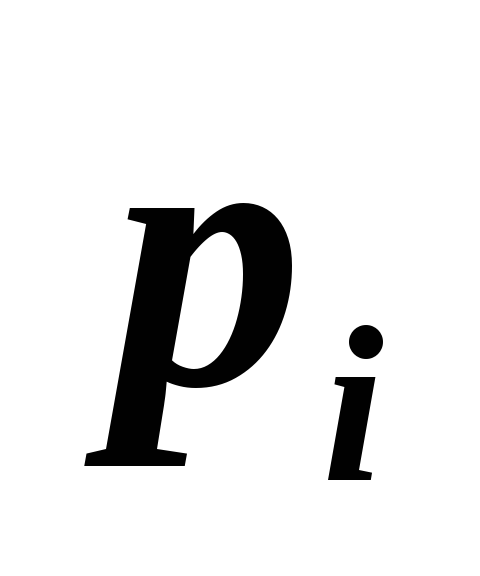9. Найти распределение вероятностей, соответствующее максимуму информационной энтропии (см. предыдущую задачу) в случае, когда для системы задано еще и среднее значение некоторого свойства G, принимающее значение в состоянии . Вычислить значение информационной энтропии, соответствующее полученному распределению и проинтерпретировать результат в случае, когда G – внутренняя энергия системы.

10. Показать, что для всех положительных x выполняется соотношение 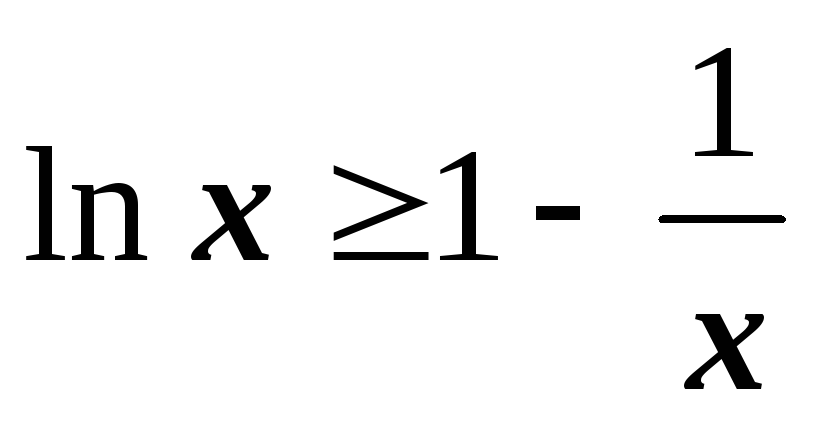, где равенство достигается только в случае x=1.

11. С точки зрения субъективной теории информации получение сведений о системе можно интерпретировать как изменение субъективных вероятностей различных состояний системы. В этом случае изменение информированности наблюдателя оценивается количеством информации Рени 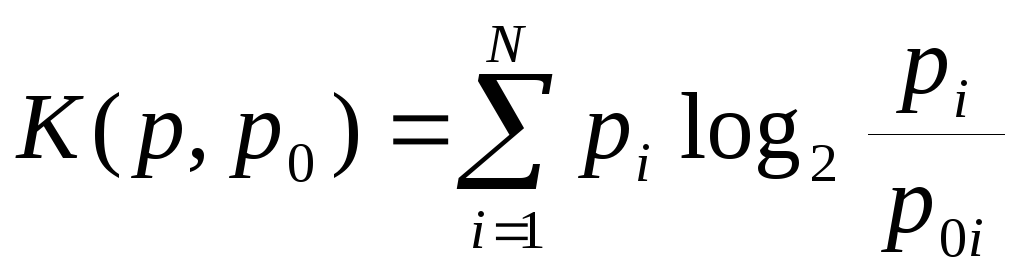, где p_0i и p_i – исходное и новое распределения вероятностей соответственно. Используя результат предыдущей задачи, доказать, что информация Рени положительно определена и интерпретировать приведенное выше соотношение при различных p_0i и p_i .