
- •Белорусский национальный технический университет
- •Практикум по курсу «Каналы передачи информации»
- •Часть 1
- •Составитель и разработчик в.В.Баркалин.
- •Тема 1: Информация и ее измерение. Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 2: Основные понятия теории вероятностей. Вычисление вероятностей составных событий Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Литература
- •Тема 3: условные вероятности Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 4: Законы распределения и числовые характеристики одномерных случайных величин Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 5: Многомерные случайные величины и условные функции распределения. Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 5: Многомерные случайные величины и условные функции распределения (продолжение). Задачи
- •Тема 6: -функция Дирака.
- •Тема 7: Преобразования одномерных случайных величин.
- •Тема 8: Преобразования многомерных случайных величин.
- •Учебно-исследовательское задание
- •Литература
- •Тема 9: энтропия и количество информации в дискретных системах Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Учебно-исследовательское задание
- •Литература
- •Тема 10: Дискретные каналы передачи информации Определения и глоссарий
- •Задания для предварительной самостоятельной подготовки
- •Тема 11: Законы распределения случайных процессов
- •Тема 12: корреляционные функции случайных процессов
- •Тема 13: спектральные плотности случайных процессов
- •Тема 14: Непрерывные системы передачи информации
- •Учебно-исследовательское задание
- •Литература
- •Содержание
Тема 13: спектральные плотности случайных процессов
Задания для предварительной самостоятельной подготовки
-
Определение и свойства преобразования Фурье. Соотношение неопределенности частота-время.
Задачи
-
Найти корреляционную функцию и спектральную плотность для стационарного случайного процесса
 с постоянными амплитудой и частотой и
начальной фазой, равномерно распоределенной
на интервале
с постоянными амплитудой и частотой и
начальной фазой, равномерно распоределенной
на интервале
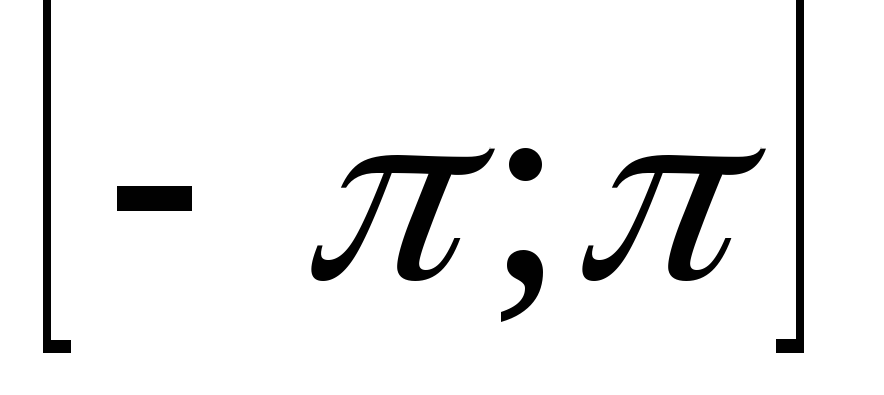 .
. -
Определить корреляционную функцию и спектральную плотность стационарного случайного процесса
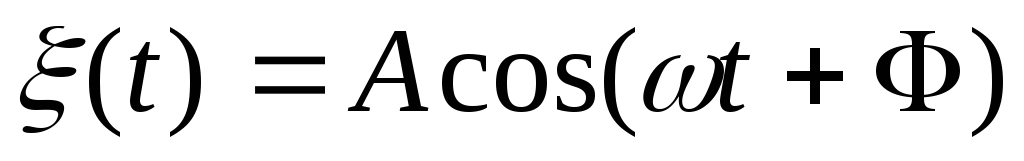 ,
где амплитуда, частота и начальная фаза
- независимые случайные величины,
амплитуда и частота заданы одномерными
плотностями
,
где амплитуда, частота и начальная фаза
- независимые случайные величины,
амплитуда и частота заданы одномерными
плотностями
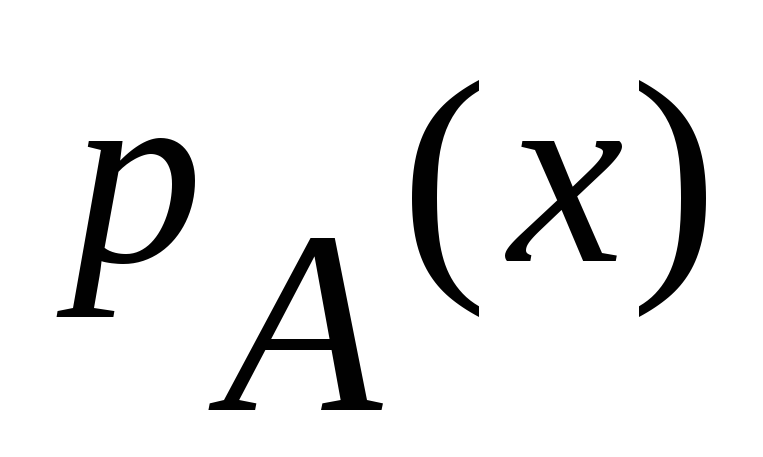 и
и
 ,
а начальная фаза равномерно распоределена
на интервале
,
а начальная фаза равномерно распоределена
на интервале
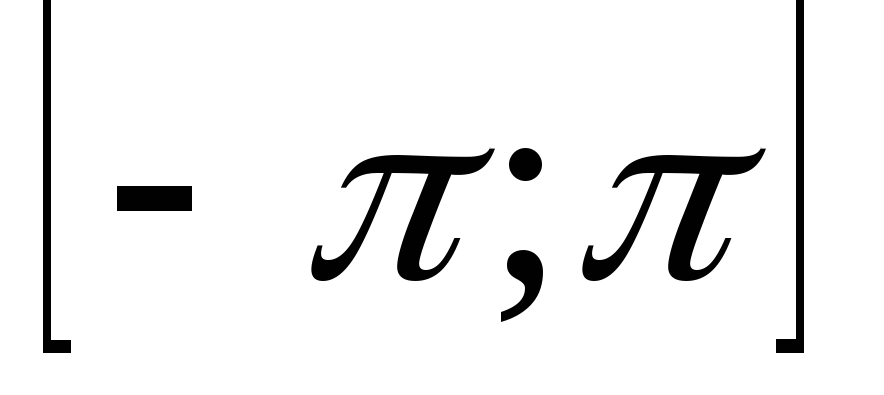 .
.
-
Выяснить разницу между спектральными плотностями стационарных случайных процессов
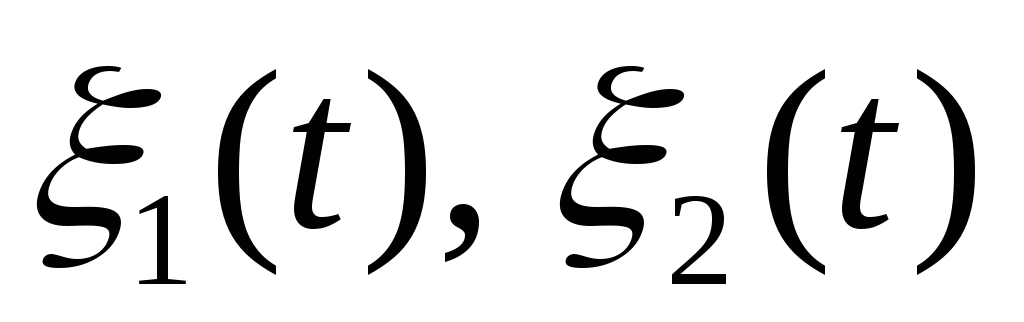 с нулевыми математическими ожиданиями
и корреляционными функциями
с нулевыми математическими ожиданиями
и корреляционными функциями
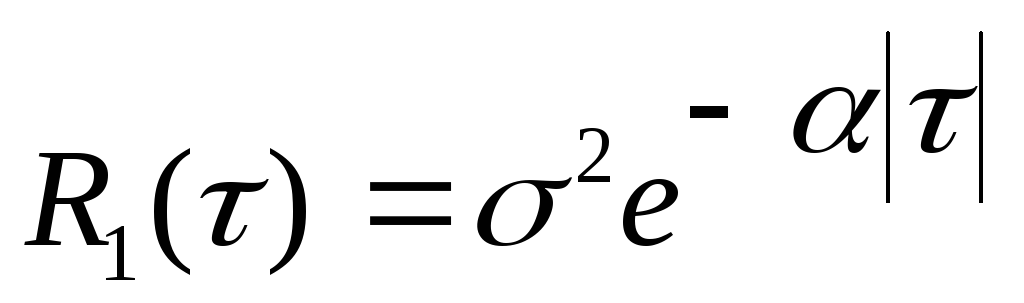 и
и
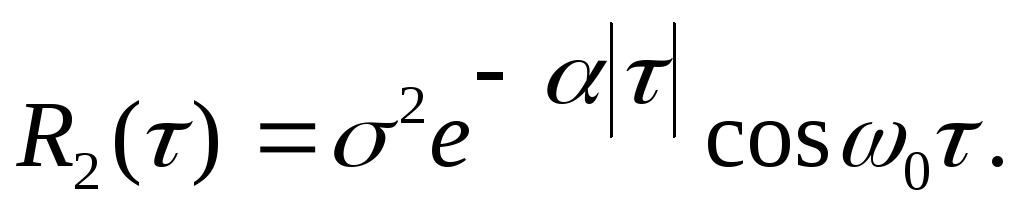
-
Найти корреляционную функцию
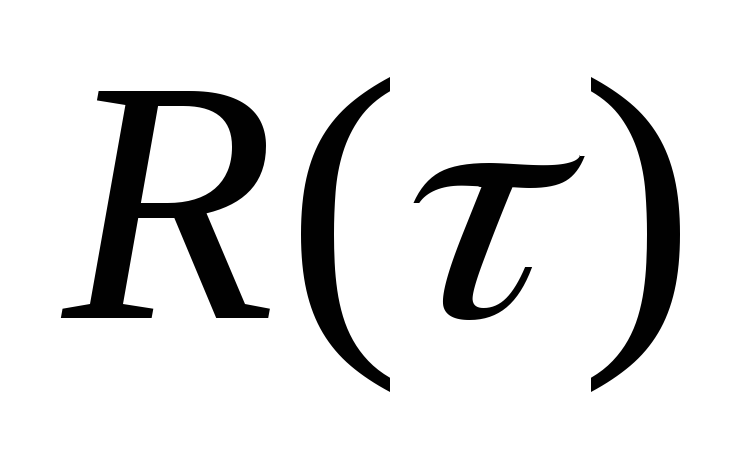 стационарного случайного процесса
стационарного случайного процесса
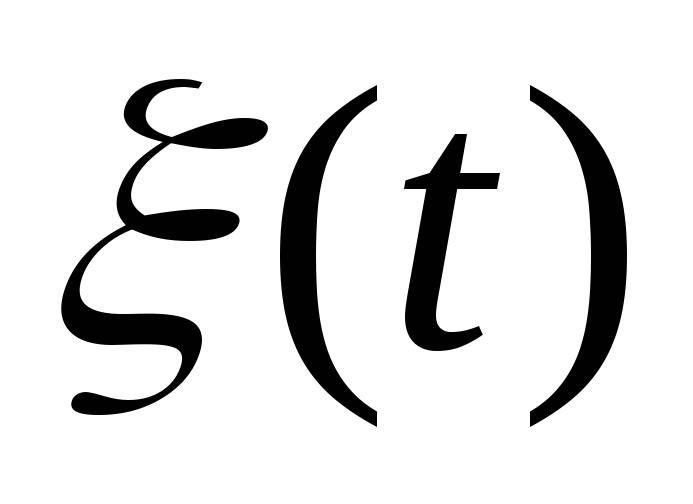 с нулевым математическим ожиданием и
спектральной плотностью
с нулевым математическим ожиданием и
спектральной плотностью
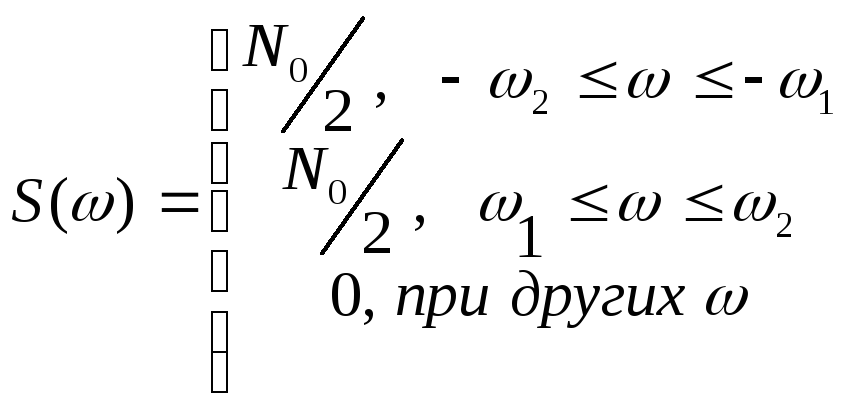
-
Определить корреляционную функцию
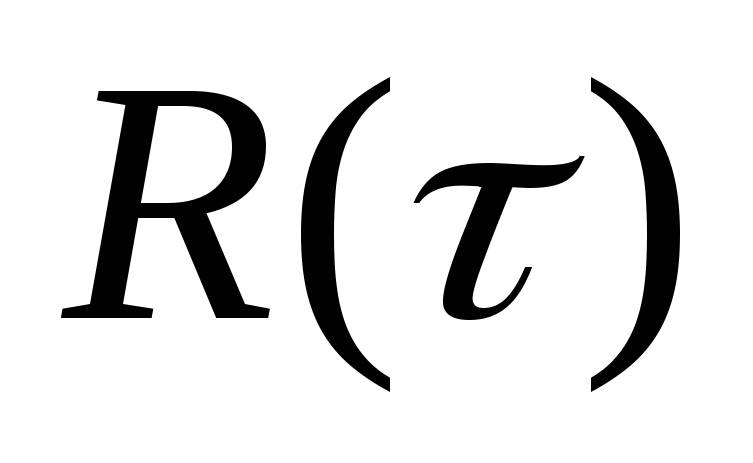 и
спектральную плотность
и
спектральную плотность
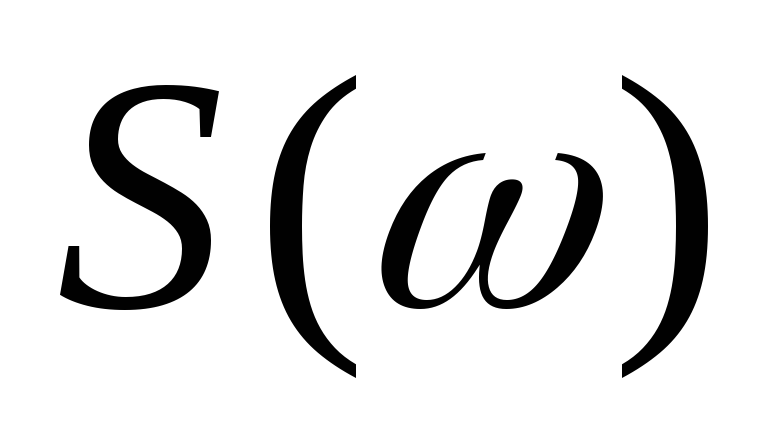 случайного
сигнала
случайного
сигнала
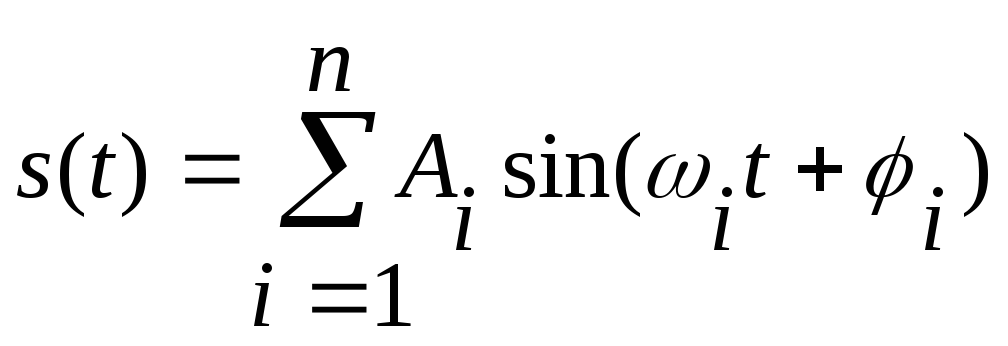 ,
где
,
где
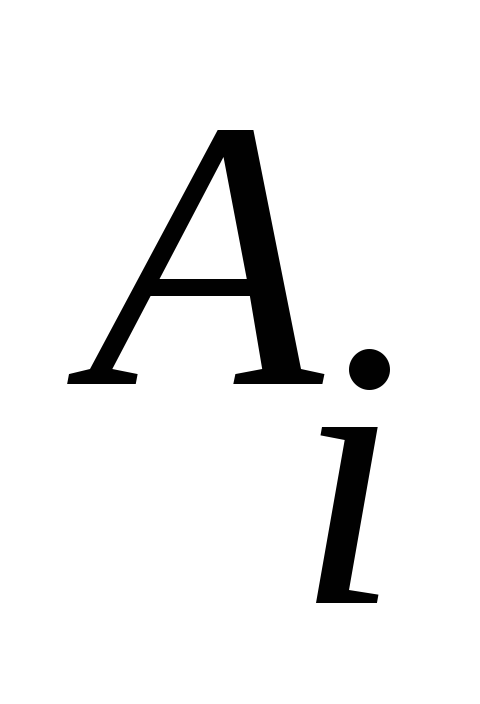 и
и
 - постоянные амплитуды и угловые частоты,
- постоянные амплитуды и угловые частоты,
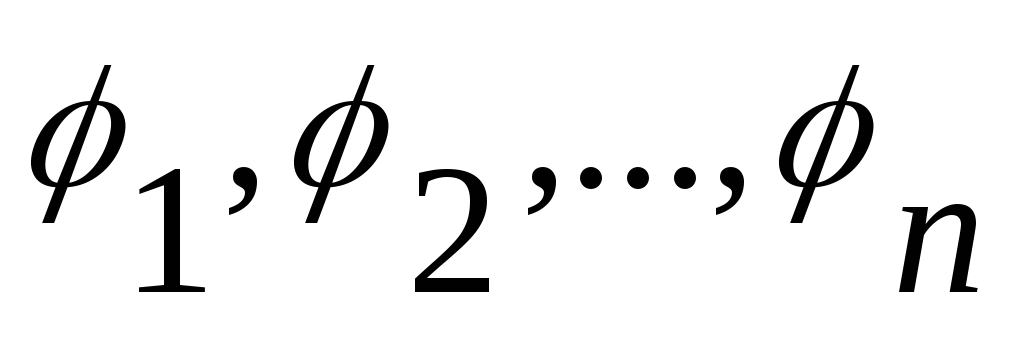 - взаимно независимые случайные начальные
фазы, равномерно распределенные на
интервале
- взаимно независимые случайные начальные
фазы, равномерно распределенные на
интервале
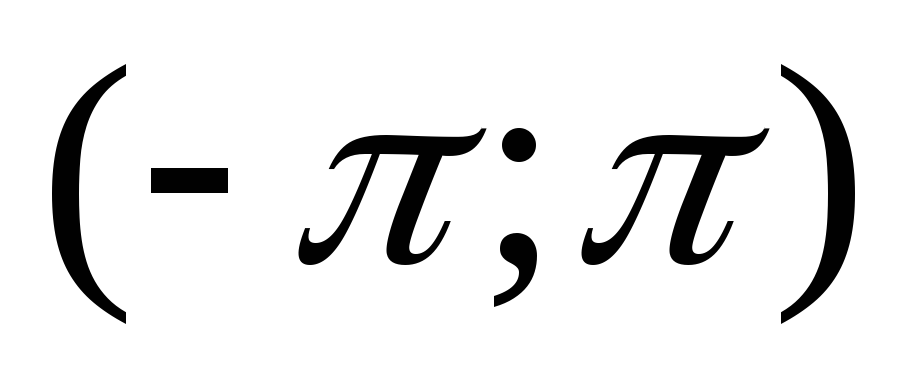 .
. -
Найти интервал корреляции
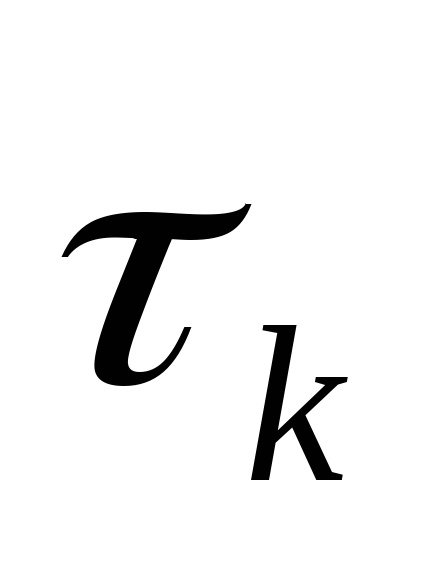 и
эффективную ширину спектра
и
эффективную ширину спектра
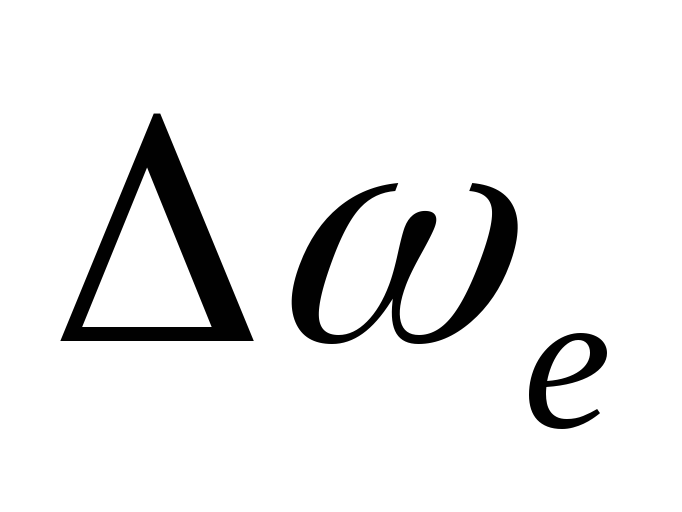 для
стационарного случайного процесса с
корреляционной функцией 1)
для
стационарного случайного процесса с
корреляционной функцией 1)
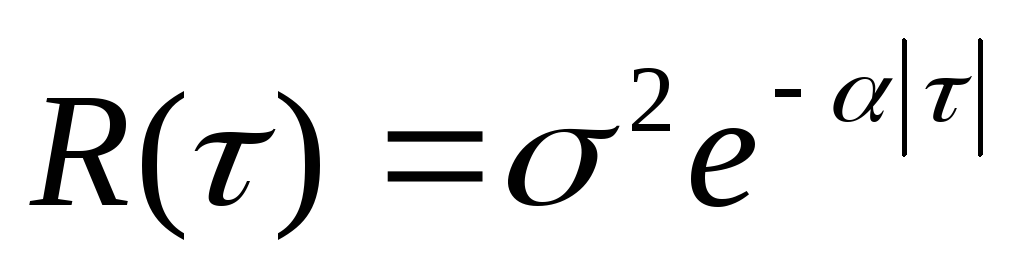 ; 2)
; 2)
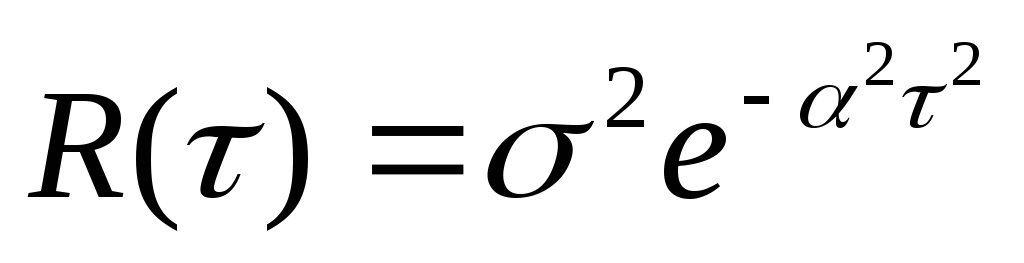 ;
3)
;
3)
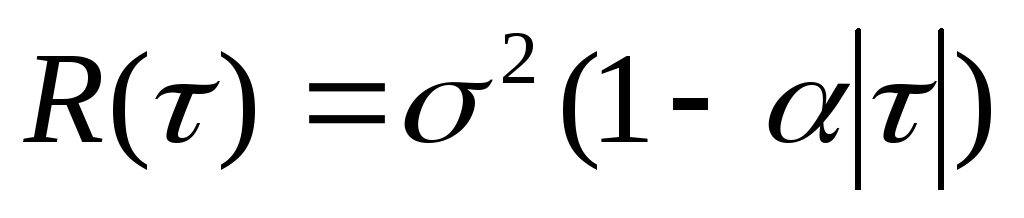 .
. -
Найти спектральную плотность стационарного случайного процесса
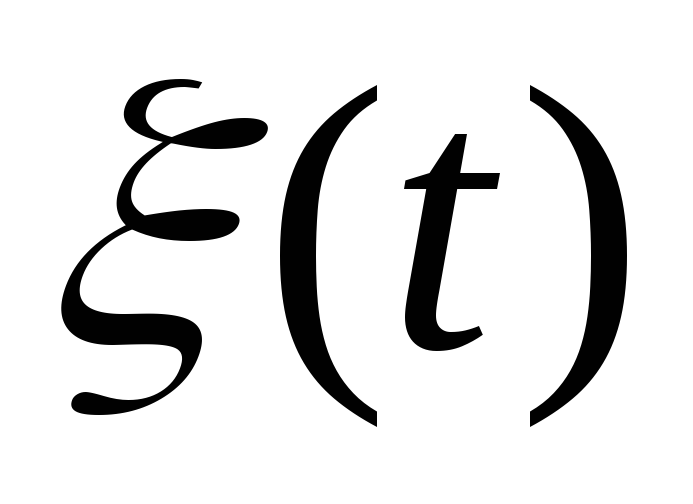 ,
корреляционная функция которого дается
выражением a)
,
корреляционная функция которого дается
выражением a)
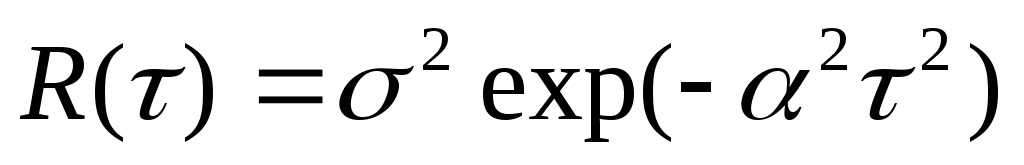 ,
б)
,
б)
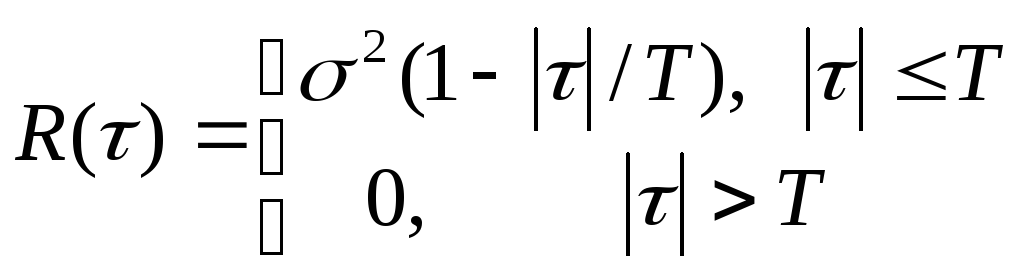 .
. -
Пусть стационарный гауссовский шум
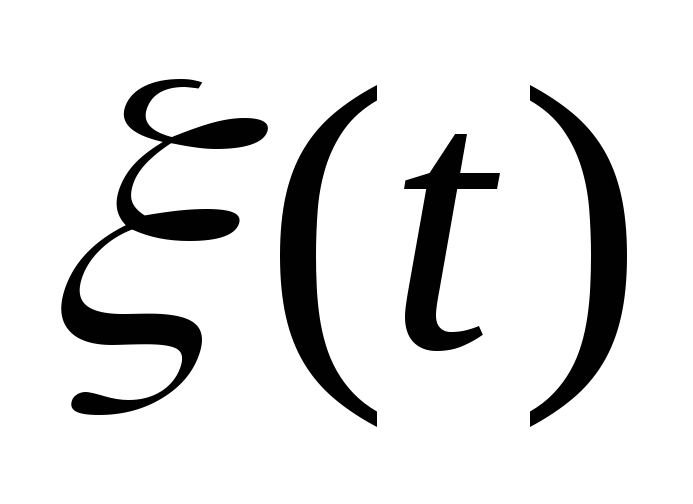 имеет равномерную спектральную плотность
в полосе шириной
имеет равномерную спектральную плотность
в полосе шириной
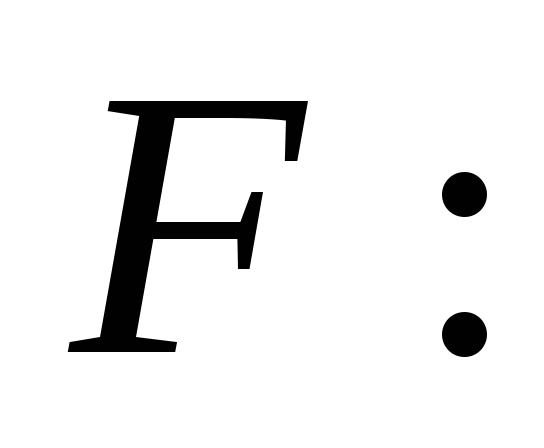
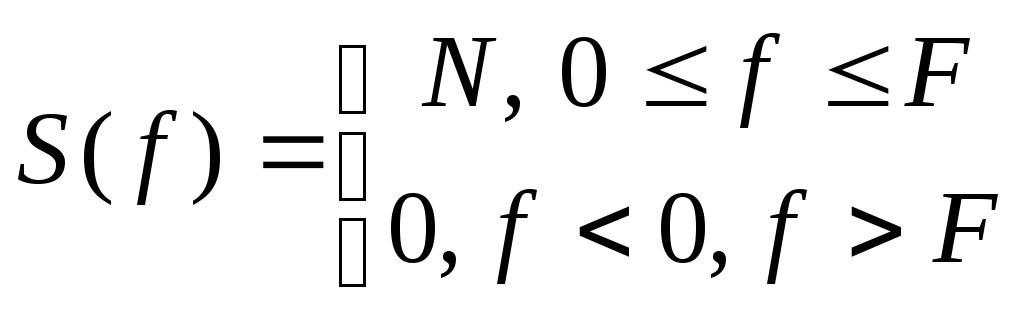 .
Доказать, что значения шума
.
Доказать, что значения шума
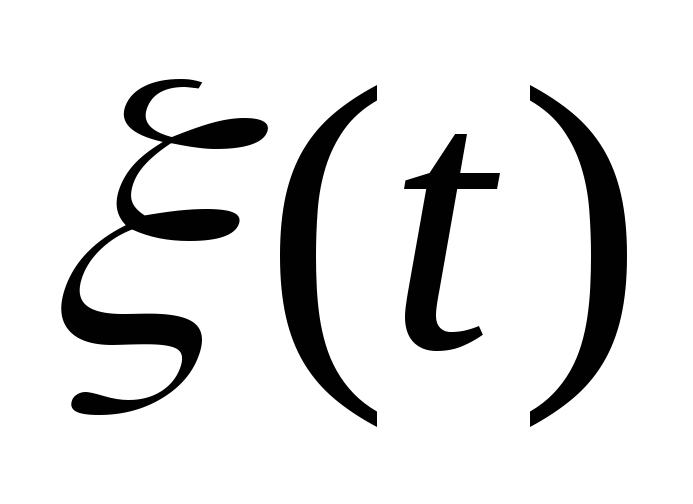 в моменты времени, отстоящие друг от
друга на величину
в моменты времени, отстоящие друг от
друга на величину
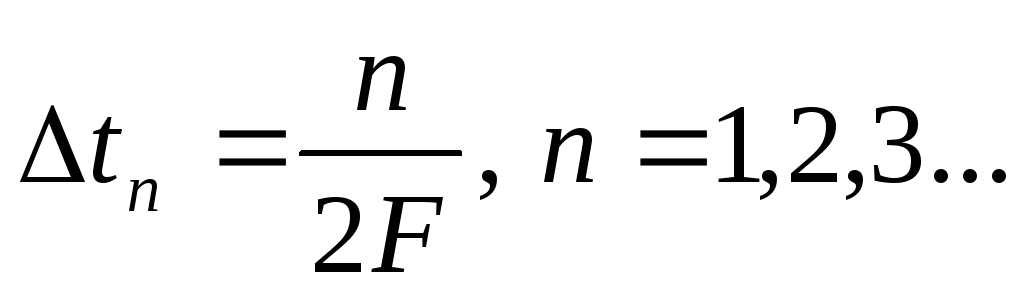 ,
статистически независимы (не
коррелированы).
,
статистически независимы (не
коррелированы). -
Случайный процесс
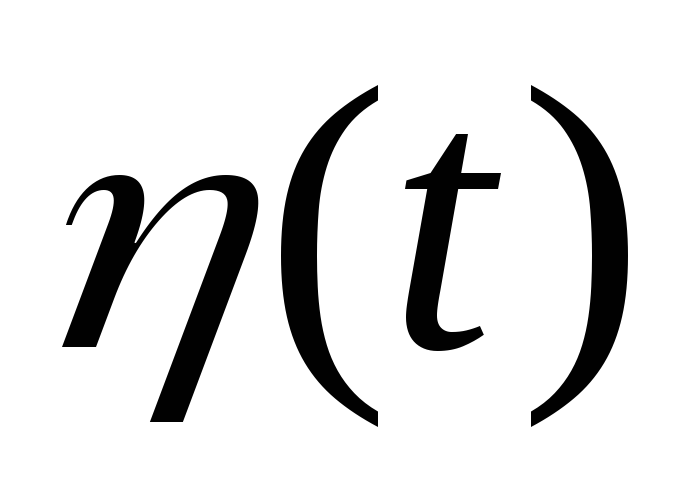 получается в результате дифференцирования
стационарного случайного процесса
получается в результате дифференцирования
стационарного случайного процесса
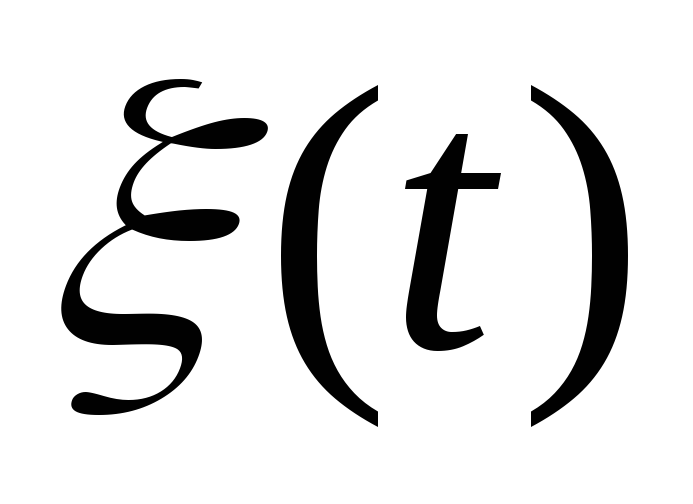 :
:
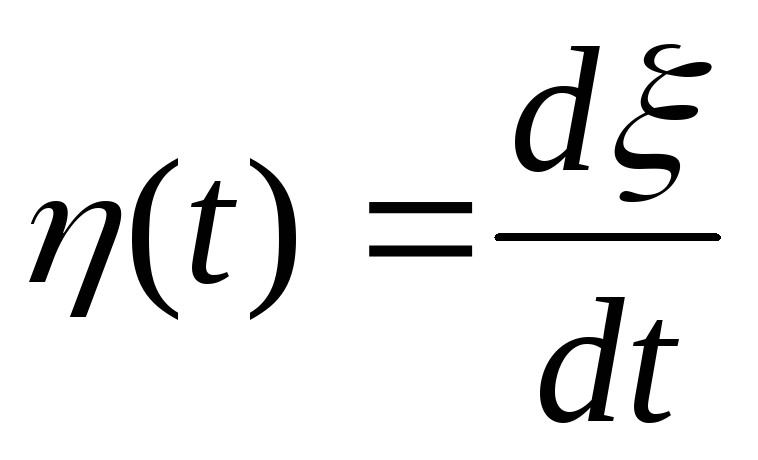 .
Определить корреляционную функцию и
спектральную плотность процесса
.
Определить корреляционную функцию и
спектральную плотность процесса
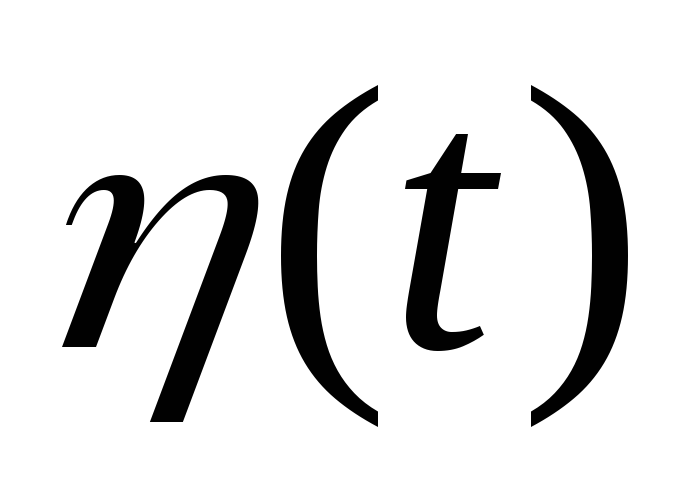 ,
если корреляционная функция процесса
,
если корреляционная функция процесса
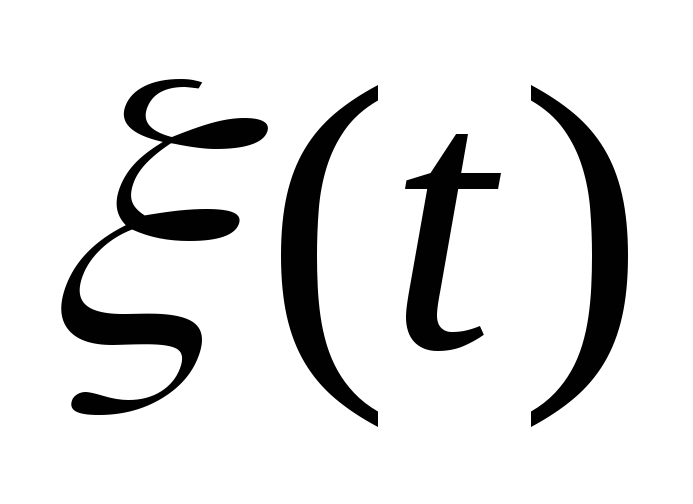 задается в виде
задается в виде
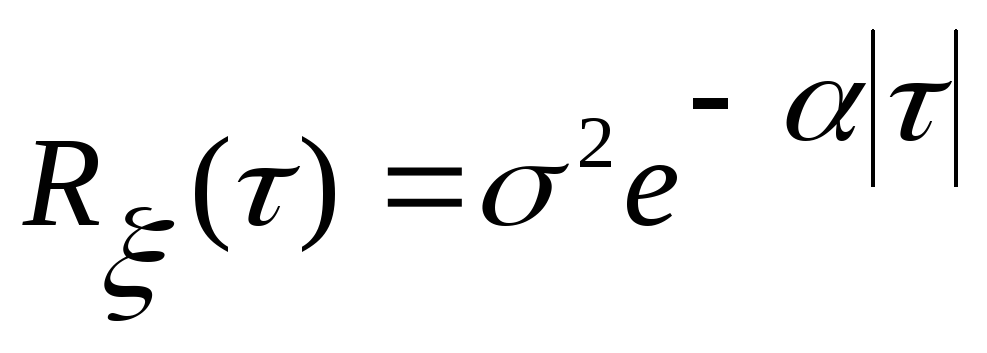 .
. -
Вычислить ковариационную функцию и спектральную плотность случайного фототелеграфного сигнала
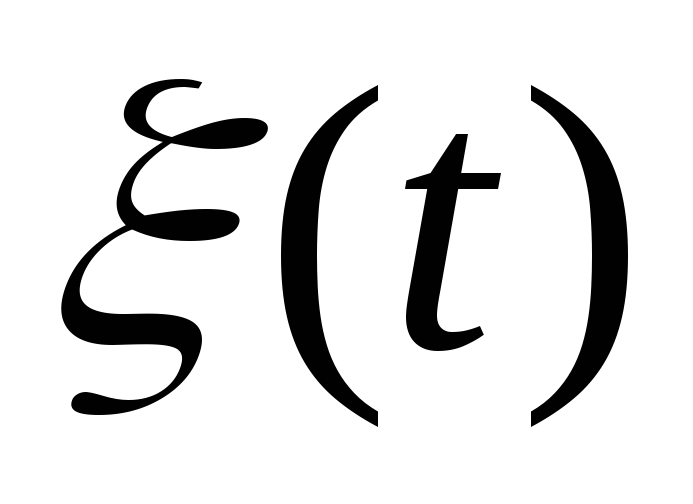 ,
сформированного на базе пуассоновского
потока упорядоченных временных точек
,
сформированного на базе пуассоновского
потока упорядоченных временных точек
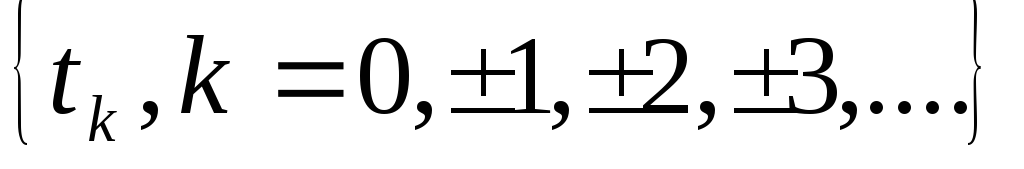 следующим образом: В интервалах между
соседними точками
следующим образом: В интервалах между
соседними точками
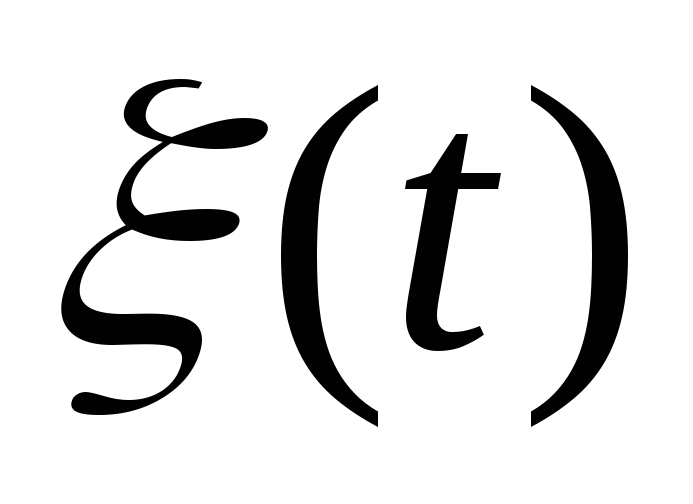 - постоянная величина, равная 1 или 0 с
вероятностями p
и (1-p)
соответственно. Значения
- постоянная величина, равная 1 или 0 с
вероятностями p
и (1-p)
соответственно. Значения
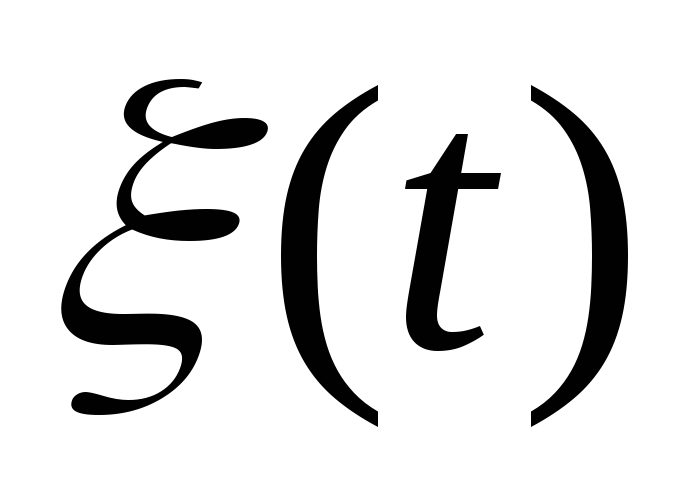 в разных интервалах независимы.
в разных интервалах независимы.
-
Вычислить корреляционную функцию и спектральную плотность стационарного случайного сигнала
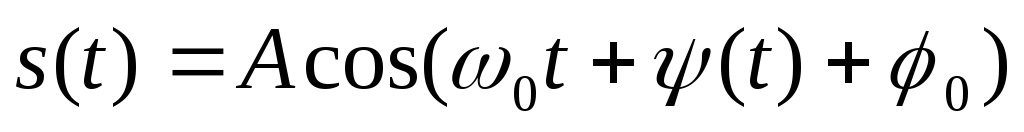 ,
у которого
,
у которого
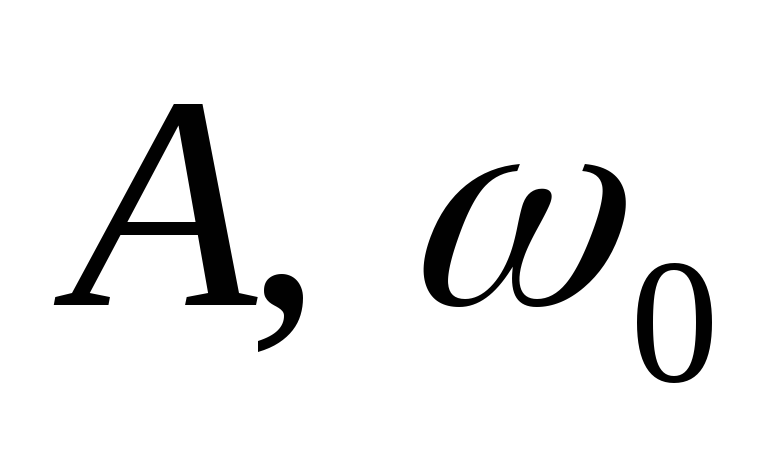 - постоянные амплитуда и частота,
- постоянные амплитуда и частота,
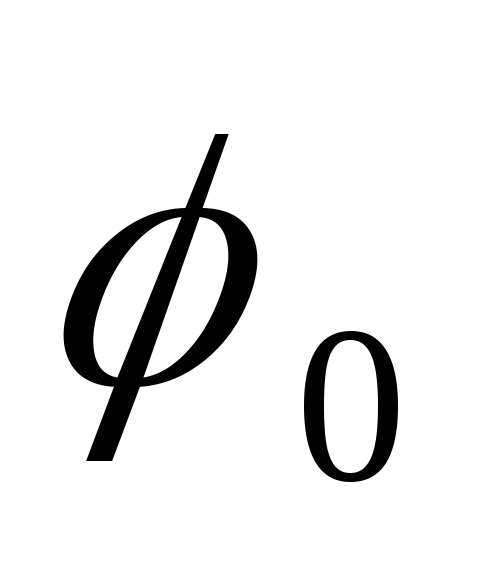 - случайна начальная фаза, равномерно
распределенная на интервале
- случайна начальная фаза, равномерно
распределенная на интервале
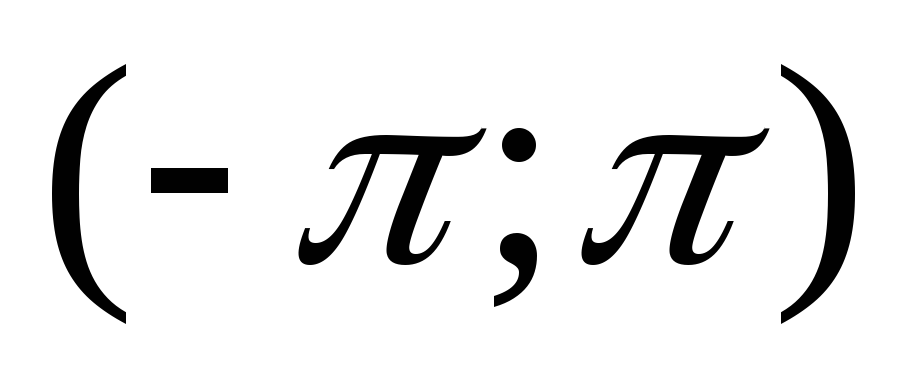 ,
,
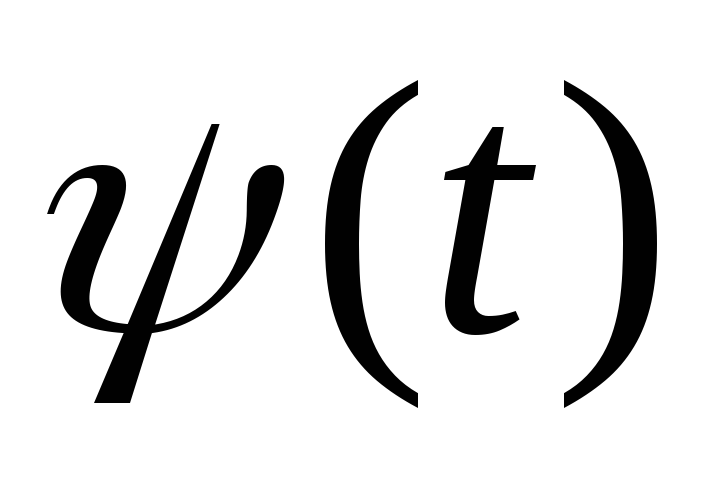 - модулирующее случайное сообщение
вида
- модулирующее случайное сообщение
вида
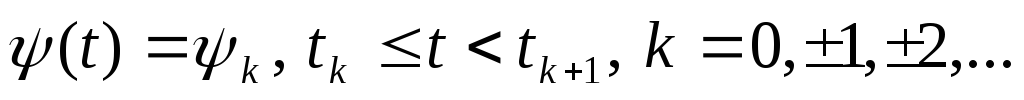 Здесь
Здесь
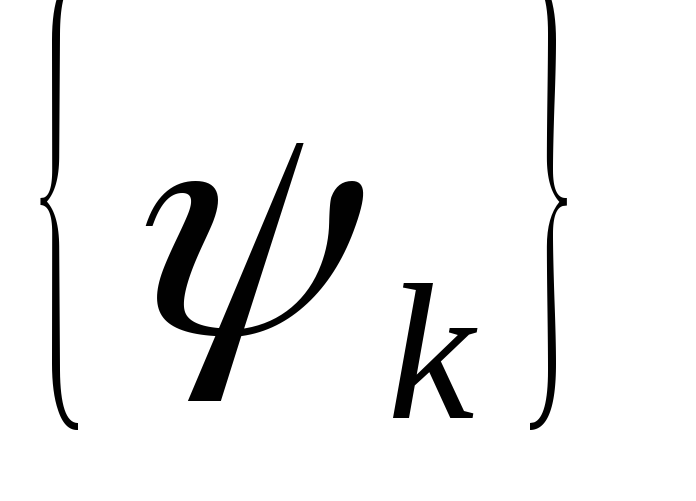 -случайная
последовательность взаимно независимых
случайных величин, равномерно
распределенных на интервале
-случайная
последовательность взаимно независимых
случайных величин, равномерно
распределенных на интервале
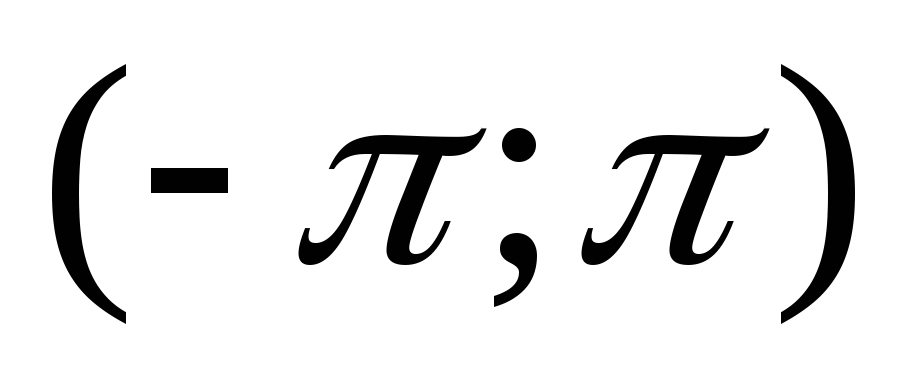 ,
,
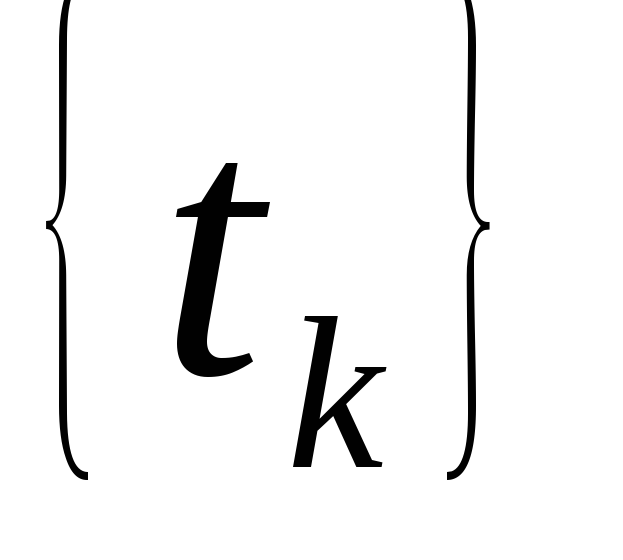 - не зависящая от
- не зависящая от
 стационарная последовательность
пуассоновских временных точек с
интенсивностью
стационарная последовательность
пуассоновских временных точек с
интенсивностью
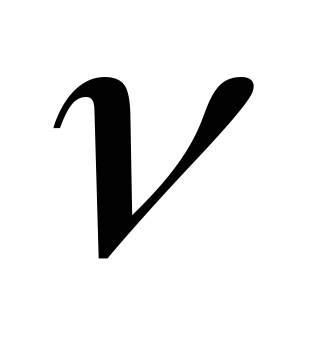 .
. -
Определить спектральную плотность случайного процесса
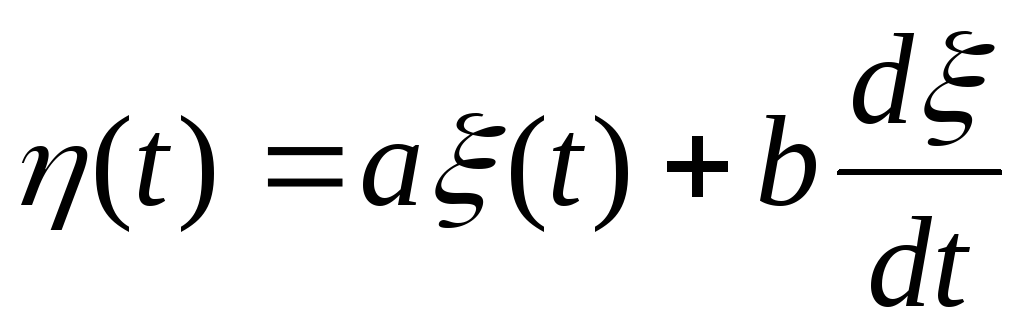 , где
, где
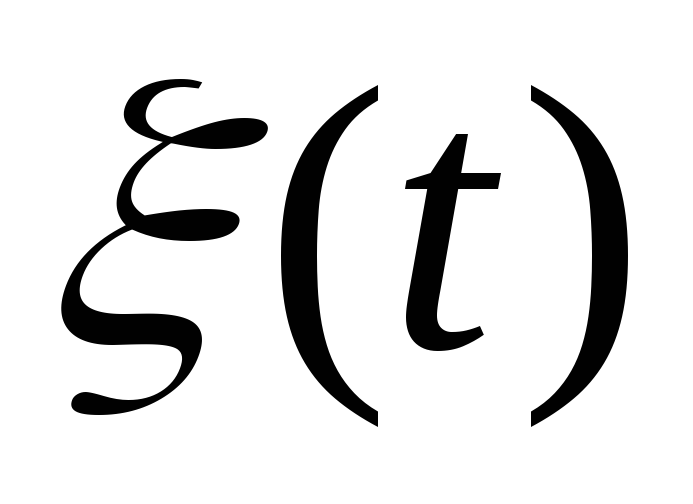 - стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
- стационарный случайный процесс с
нулевым математическим ожиданием и
корреляционной функцией
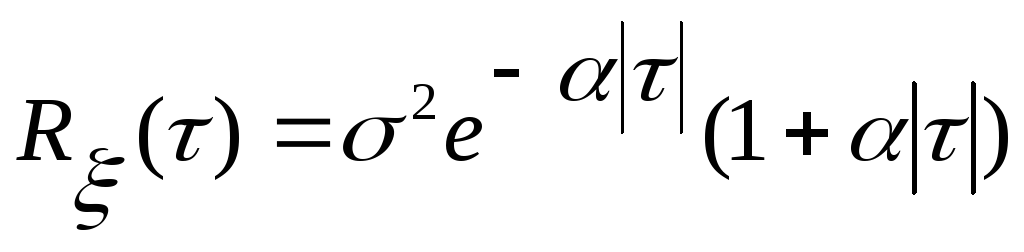 .
. -
Определить корреляционную функцию
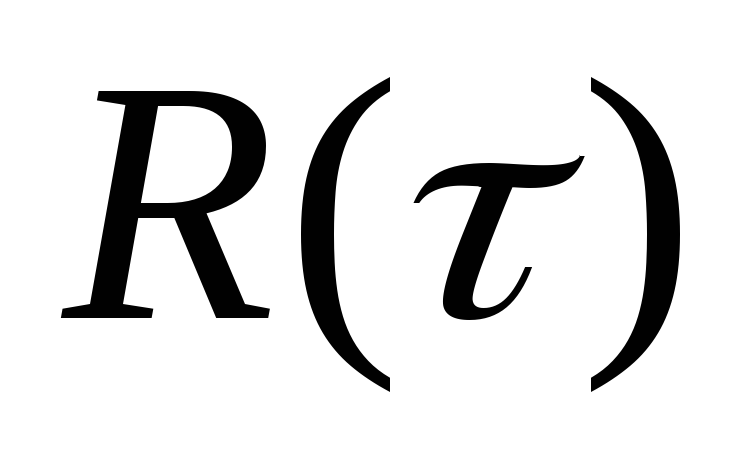 и
спектральную плотность
и
спектральную плотность
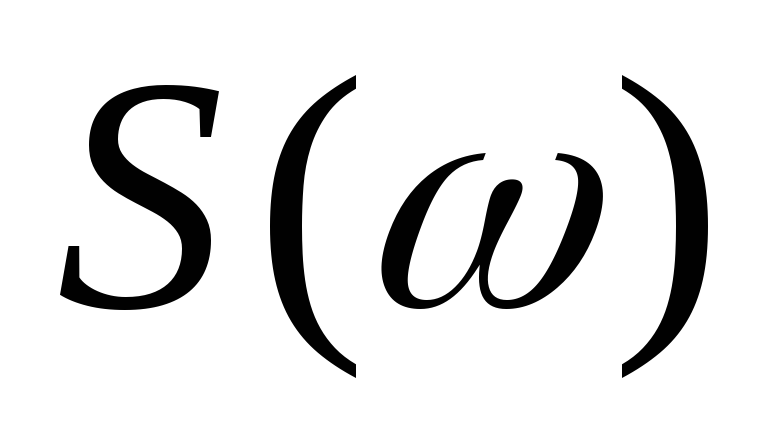 случайного
сигнала
случайного
сигнала
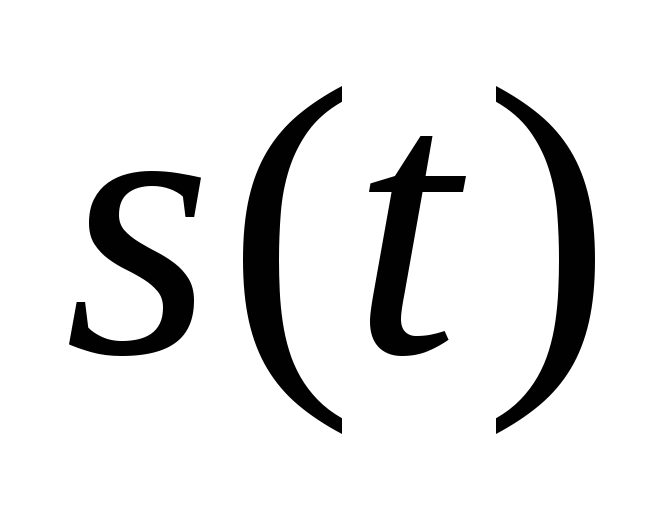 ,
отраженного от объекта, движущегося с
относительной скоростью
,
отраженного от объекта, движущегося с
относительной скоростью
 относительно
приемника. Сигнал имеет вид
относительно
приемника. Сигнал имеет вид
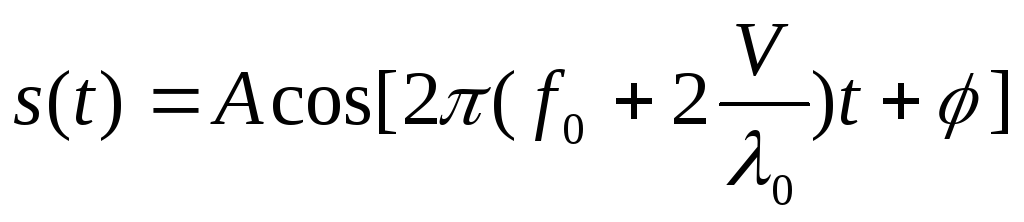 ,
где
,
где
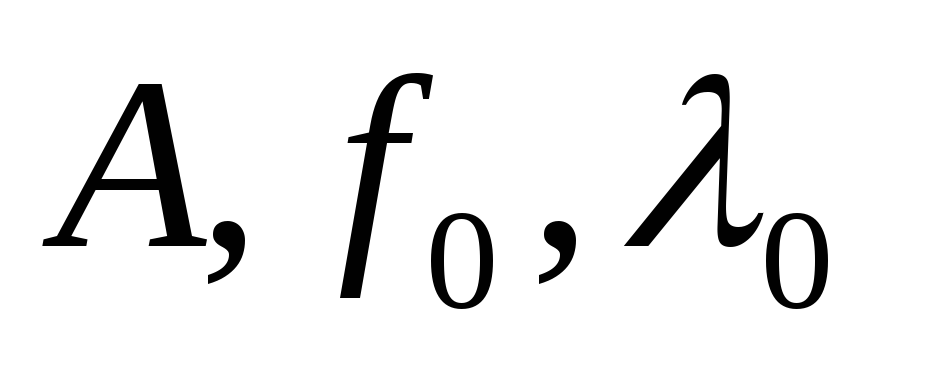 -
постоянные амплитуда, несущая частота
и длина волны электромагнитных колебаний,
-
постоянные амплитуда, несущая частота
и длина волны электромагнитных колебаний,
 -
случайна начальная фаза, равномерно
распределенная на интервале
-
случайна начальная фаза, равномерно
распределенная на интервале
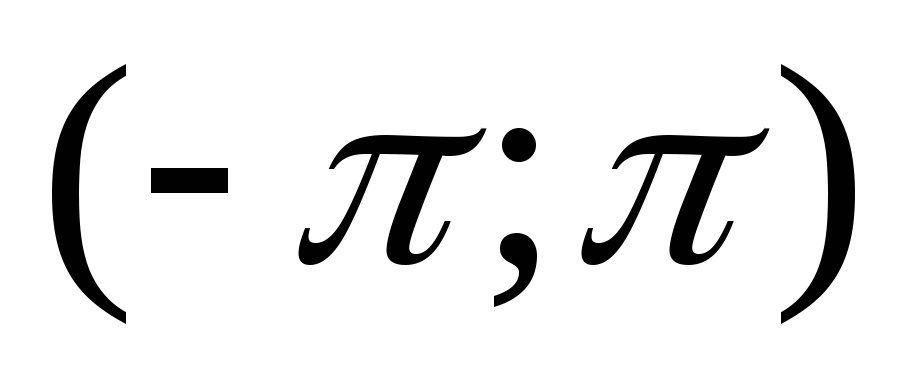 .
Относительно скорости
.
Относительно скорости
 предполагается,
что она представляет собой случайную
величину, равномерно распределенную
в интервале
предполагается,
что она представляет собой случайную
величину, равномерно распределенную
в интервале
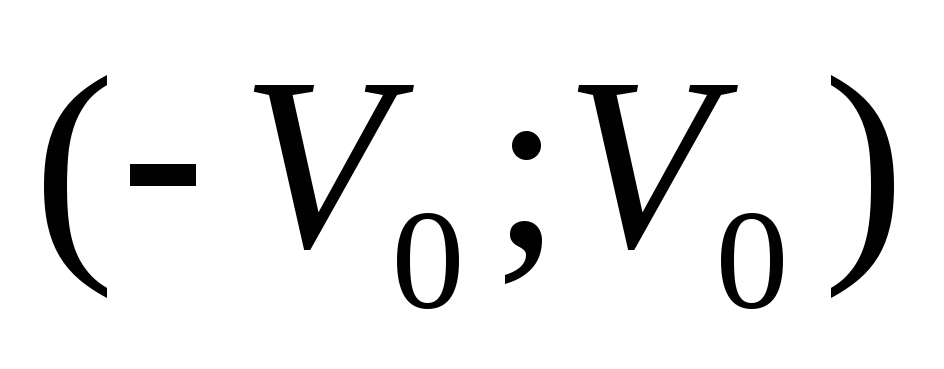 .
.
Учебно-исследовательское задание
-
Устойчивость и равновесие фаз в термодинамических системах. Понятио критического состояния.
-
Поверхности раздела фаз в термодинамических системах.
Литература
-
В.И.Тихонов. Статистическая радиотехника. М.: Радио и Связь, 1982.
-
В.Т.Горяинов, А.Г.Журавлев, В.И.Тихонов. Статистическая радиотехника. Примеры и задачи. М.: Сов.Радио, 1980.
-
Д.Д.Кловский, В.А.Шилкин. Теория передачи сигналов в задачах. М.: Связь, 1978.
Практическое занятие 16.
