1.1.2. Закон Джоуля–Ленца

С прохождением тока через проводник, обладающий сопротивлением, неразрывно связано выделение теплоты (нагревание проводника). Задача состоит в том, чтобы найти количество теплоты, выделяющееся за единицу времени на определенном участке цепи. Здесь возможны два случая, которые и рассматриваются последовательно – однородный и неоднородный участки цепи. При решении этого вопроса используются закон сохранения энергии и закон Ома.

П

Рис. 1.1

усть участок рассмотрения задачи заключен между сечениями 1 и 2 проводника (рис. 1.1).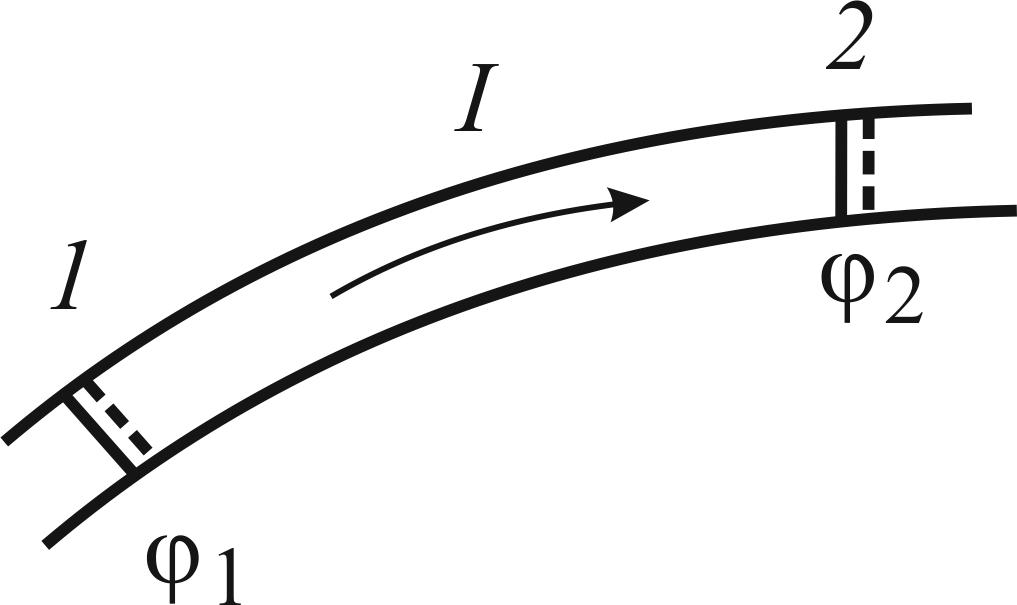

Найдем работу, которую совершают силы поля над носителями тока на участке 1–2 за время dt. Если сила тока в проводнике равна I, то за время dt через каждое сечение проводников 1 и 2 пройдет заряд Так как распределение зарядов в проводнике остается при этом неизменным (ток постоянный), то весь процесс эквивалентен непосредственному переносу заряда q от сечения 1 к сечению 2, имеющим потенциалы и . Поэтому совершаемая при таком переносе работа сил поля

Согласно закону сохранения энергии, эквивалентная этой работе энергия должна выделяться в иной форме. Если проводник неподвижен и в нем не происходят химические превращения, то эта энергия должна выделяться в форме внутренней (тепловой) энергии, в результате чего проводник нагревается. Механизм этого превращения достаточно прост: носители тока (например, электроны в металлах) в результате работы сил поля приобретают дополнительную кинетическую энергию и затем расходуют ее на возбуждение колебаний решетки при столкновении с ее узлами-атомами.

Итак, согласно закону сохранения энергии, элементарная работа где P – теплота, выделяемая в единицу времени (тепловая мощность). Из сравнения последнего равенства с предыдущим получаем а так как по закону Ома то

(1.9)

Данная формула выражает известный закон Джоуля–Ленца.

Получим выражение этого закона в локальной форме, характеризующей выделение теплоты в различных местах проводящей среды. Для этой цели выделим в данной среде элементарный объем в виде цилиндрика с образующими, параллельными вектору – плотности тока в данном месте. Пусть поперечное сечение цилиндрика равно dS, а его длина – dl. Тогда на основании (1.9) в данном объеме за время dt выделяется количество теплоты

где – объем цилиндрика. Разделив последнее уравнение на dVdt, получим формулу, которая определяет количество теплоты, выделяющееся за единицу времени в единице объема проводящей среды, – удельную тепловую мощность тока:

(1.10)

Эта формула выражает закон Джоуля–Ленца в локальной форме: удельная тепловая мощность тока w пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке.

Уравнение (1.10) представляет собой наиболее общую форму закона Джоуля–Ленца, применимую к любым проводникам вне зависимости от их формы, однородности и от природы сил, возбуждающих электрический ток. Если на носители тока действуют только электрические силы, то на основании закона Ома (1.3)

(1.11)

Таким образом, последнее уравнение имеет менее общий характер, нежели (1.10).

Если участок цепи содержит источник ЭДС, то на носители тока будут действовать не только электрические силы, но и сторонние. Тогда выделяемое в неподвижном проводнике тепло будет равно по закону сохранения энергии алгебраической сумме работ электрических и сторонних сил. Это же относится и к соответствующим мощностям: тепловая мощность должна быть равна алгебраической сумме мощностей электрических и сторонних сил, в чем можно убедиться, умножив выражение (1.8) на I:

(1.12)

Здесь слева стоит выделяющаяся на участке тепловая мощность P; при наличии сторонних сил величина P определяется той же формулой, что и для однородного участка цепи. Последнее же слагаемое справа представляет собой мощность, развиваемую сторонними силами на данном участке. Заметим еще, что последняя величина (EI) является алгебраической: в отличие от _, она изменяет знак при изменении направления тока I.

Таким образом, уравнение (1.12) означает, что тепловая мощность, выделяемая на участке цепи между точками 1 и 2, равна алгебраической сумме мощностей электрических и сторонних сил.

Получим теперь уравнение (1.12) в локальной форме. Для этого умножим обе части уравнения (1.4) на j, а также учтем, что и (см. (1.10)). Тогда удельная тепловая мощность тока в неоднородной проводящей среде

(1.13)