Xn,xk,yn,h,X,y:real;

I:integer;

Function f(x,y:real):real;

begin

{Здесь приводим выражение для вычисления функции f(x,y) }

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y методом Эйлера ');

{ Ввод исходных данных }

xn:=0; yn:=1; xk:=1; h:=0.1;

{ Выводим шапку таблицы и первую точку }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

{ Начинаем расчет }

x:=xn; y:=yn; i:=1;

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

repeat

y:=y+h*f(x,y);

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

x:=x+h;

i:=i+1;

until x>xk;

Writeln('--------------------');

Readln;

End.

26. Численные методы решения обыкновенных дифференциальных уравнений. Модифицированный метод Эйлера.

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала по методу Эйлера вычисляется значение функции в следующей точке:

y*_i+1 = y_i + h*f(x_i,y_i)

Оно используется для вычисления приближённого значения производной в конце интервала f(_i+1, y*_i+1). Вычислив среднее между этим значением производной и её значением в начале интервала, найдём более точное значение y_i+1:

y_i+1 = y_i + h/2*[f(x_i,y_i) + f(x_i+1, y*_i+1)] .

Принцип метода проиллюстрирован на рисунке. Для получения новой точки в нём требуется информация о двух других точках – предыдущей и промежуточной.

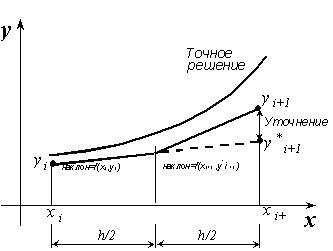
Ошибка этого метода на каждом шаге имеет порядок h².

Пример: Разработать, сохранить и выполнить программу для решения дифференциального уравнения из предыдущего примера (раздел 25) модифицированным методом Эйлера. При выполнении расчетов использовать хранение результатов в массивах.

Program ModEuler;

Uses Crt;

Var

Xn,xk,yn,yw,h:real;

I,n:integer;

X,y:array [1..20] of real;

Function f(x,y:real):real;

begin

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y модифицированным методом Эйлера ');

xn:=0; yn:=1; xk:=1; h:=0.1;

x[1]:=xn; y[1]:=yn; i:=1;

repeat

yw:=y[i]+h*f(x[i],y[i]);

y[i+1]:=y[i]+h/2*(f(x[i],y[i])+f(x[i]+h,yw));

x[i+1]:=x[i]+h;

i:=i+1;

until x[i]>xk;

n:=i;

{ Выводим результаты }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

for i:= 1 to n do

Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |');

Writeln('--------------------');

Readln;

End.

27. Численные методы решения обыкновенных дифференциальных уравнений. Метод Рунге-Кутта.

Для повышения точности вычисления значений функции требуется проведение дополнительных вычислений внутри интервала h, то есть между x_i и x_i+1. Метод Рунге-Кутта даёт набор формул для расчёта координат внутренних точек, требуемых для достижения точности, то есть ошибки на каждом шаге, порядка h₄. Расчёты при использовании этого метода производятся по формуле

y_i+1=y_i+(k₀+2k₁+2k₂+k₃)/6

Здесь k₀=h*f(x_i,y_i), k₁=h*f(x_i+h/2, y_i+k₀/2), k₂=h*f(x_i+h/2, y_i+k₁/2), k3=h*f(x_i+h, y_i+k₂)

Метод Эйлера и его модификация по существу являются методами Рунге-Кутта первого и второго порядка соответственно. По сравнению с ними метод Рунге-Кутта обеспечивает более высокую точность, что позволяет увеличить шаг интегрирования h. Допустимая погрешность на шаге определяет его максимальную величину.

Пример: Приведём фрагмент программы для решения дифференциального уравнения из предыдущего примера (раздел 26) методом Рунге-Кутта.

Program Runge;

Uses Crt;

Var