22. Численные методы решения нелинейных уравнений. Метод Ньютона (метод касательных).
В отличие от метода половинного деления, для определения интервала, в котором заключён корень, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции, в методе Ньютона делается экстраполяция с помощью касательной к кривой в данной точке. В основе метода лежит разложение функции f(x) в ряд Тейлора:
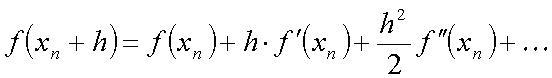
Члены ряда, содержащие h во второй и более высоких степенях, отбрасываются; используется соотношение xn+h=xn+1. Предполагается, что переход от xn к xn+1 приближает значение функции к нулю так, что f(xn+h)=0. Тогда xn+1=xn-f(xn)/f'(xn).
Значение xn+1 соответствует точке, в которой касательная к кривой в точке xn пересекает ось x. Так как кривая f(x) отлична от прямой, то значение функции f(xn+1) не будет в точности равно нулю. Поэтому вся процедура пoвторяется, причём вместо xn используется xn+1. Счет прекращается, когда разница между xn и xn+1 будет меньше или равна числу ε, т.е. |xn-xn+1|=<ε. На рисунке процесс решения уравнения методом Ньютона показан графически.
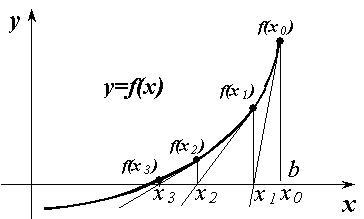
Пример: Приведём фрагменты текста программы, которая решает задачу из предыдущего примера (раздел 21) методом касательных. Ввод и вывод результатов подробно разобран выше.
Program Kasat;
Uses Crt, Printer;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Function f1(x:real):real;
begin
{ Здесь приводим выражение для производной функции }
f:=3*x*x+2*x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом касательных');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
x:=a;
Repeat
t:=f(x)/f1(x);
x:=x-t;
Until abs(t)<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.
Метод Ньютона требует меньшего числа повторений, чем метод половинного деления. Недостатки метода – необходимость дифференцирования функции f(x), и f(x) должно быть не равно нулю.
23. Численные методы решения нелинейных уравнений. Метод хорд (метод ложного положения).
В основе метода лежит линейная интерполяция по двум значениям функции f(x), имеющим противоположные знаки. Через точки, соединяющие значения функции f(a) и f(b) на концах отрезка [a,b], проводят прямую, которая пересекает ось x в точке
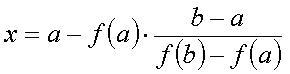
Значение функции f(x) сравнивается со значениями функций f(a) и f(b) и в дальнейшем используется вместо того из них, с которым оно совпадает по знаку. Если значение f(x) недостаточно близко к нулю, то вся процедура повторяется до тех пор, пока не будет достигнута необходимая степень сходимости ε. На рисунке процесс решения показан графически.
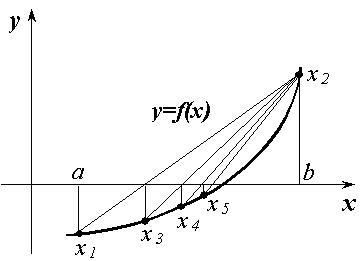
Пример: Приведём фрагменты текста программы, которая решает задачу из предыдущего примера (раздел 22) методом хорд.
Program Horda;
Uses Crt;
Var
a,b,t,x,eps:real;
Function f(x:real):real;
begin
{Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом хорд');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
{ Начинаем расчет }
Repeat
x:=a-f(a)*(b-a)/(f(b)-f(a));
if f(a)*f(x)<=0 then b:=x
else a:=x;
Until abs(f(x))<=eps;
Writeln(' Уравнение имеет корень x = ', x:10:8);
Readln;
End.