лекции / УравнМех

Физическими свойствами жидкостей, лежащими в основе построения теоретических моделей, является непрерывность (cплошность) и легкая подвижность (текучесть). Под сплошностью понимается непрерывное распределение в пространстве физических параметров, характеризующих жидкость, а под текучестью - слабое противодействие жидкостей даже сколь угодно малым силам, вызывающим относительное скольжение частиц жидкости. В то же время большинство рабочих жидкостей оказывает значительное сопротивление сжатию, и они практически не изменяют свой объем под действием всесторонних сил давления, нормальных к поверхности, ограничивающей рассматриваемый объем. Для описания движения несжимаемой жидкости, обладающей сплошностью и текучестью, а также вязкостью, характеризующей внутреннее трение в жидкости, пользуются уравнением неразрывности и уравнениями Навье-Стокса, которые являются следствием применения законов сохранения массы и количества движения к элементарному объему жидкости. Решение этих уравнений в общем случае сложно и может быть доведено до конца лишь в отдельных частных случаях и при следующих упрощающих предположениях: ламинарное течение, введение начальных и граничных условий, рассмотрение протекания процессов в стационарных режимах.

Исходя из уравнений Стокса и уравнения неразрывности получим, что если провести нормальные к оси трубы сечения, то во всех таких сечениях распределения скоростей одинаковы, а давление меняется только от сечения к сечению, сохраняя в данном сечении одно значение (установившееся движение). При установившемся движении вязкой жидкости по цилиндрической трубе перепад давления, умноженный на площадь сечения играет роль движущей силы, уравновешиваемой силами сопротивлений трения жидкости о стенки трубы. Сами токи в среде и вызываемые ими искажения магнитного поля определяются уравнениями Максвелла. Таким образом, уравнения гидродинамики и электродинамики оказываются взаимосвязанными.

Рассмотрим особенности движения жидкости в трубах круглого сечения.

Существуют два вида движения жидкости: упорядоченное или ламинарное движение, при котором отдельные слои жидкости скользят друг относительно друга, не смешиваясь между собой, и неупорядоченное, турбулентное движение, когда частицы жидкости движутся по сложным, все время изменяющимся траекториям, и в жидкости происходит интенсивное перемешивание. / /

Известно, что вязкие жидкости (масла) движутся большей частью упорядоченно, а маловязкие жидкости (вода) почти всегда неупорядоченно. Основная особенность турбулентного движения жидкости заключается в наличии поперечных к направлению движения составляющих скорости, накладывающихся на основную скорость в продольном направлении.

Переход от ламинарного течения к турбулентному происходит при определенной скорости (так называемая критическая скорость), которая для труб разных диаметров оказывается различной, возрастающей с увеличением вязкости и уменьшающейся с уменьшением диаметра трубы. / /

Установлены условия, при которых возможны существование ламинарного и турбулентного режима движения жидкости и переход от одного режима к другому. Состояние (режим) потока жидкости в трубе зависит от величины безразмерного числа, которое учитывает основные факторы, определяющие это движение: среднюю скорость υ, диаметр трубы d, плотность жидкости ρ₁ и ее абсолютную вязкость λ.

, (2.1)

где ν – кинематический коэффициент вязкости, м²/с

Величина d в числе Рейнольдса может быть заменена любым линейным параметром, связанным с условиями течения или обтекания (диаметр трубы, диаметр падающего в жидкости шара, длина обтекаемой жидкостью пластинки). Значение числа Рейнольдса, при котором происходит переход от ламинарного движения к турбулентному, называют критическим числом Рейнольдса и обозначают Re_кp. Его величина зависит от условий входа в трубу, шероховатости ее стенок, отсутствия или наличия первоначальных возмущений в жидкости, конвекционных токов и др.

При Re > Re_кp режим движения является турбулентным, при Re < Re_кp — ламинарным. Наиболее часто в расчетах принимают для критического числа Рейнольдса значение Re_кp = 2000, отвечающее переходу движения жидкости из турбулентного в ламинарное; при переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину (для хорошо закругленного плавного входа оно может быть доведено до 20 000). Исследования показывают, что критическое значение числа Рейнольдса увеличивается в сужающихся трубах и уменьшается в расширяющихся. Это объясняется тем, что при ускорении движения частиц жидкости в сужающихся трубах их тенденция к поперечному перемешиванию уменьшается, а при замедленном течении в расширяющихся трубах усиливается.

По критическому значению числа Рейнольдса можно найти критическую скорость, такую, ниже которой всегда будет иметь место ламинарное движение жидкости:

(2.2)

Ламинарный режим для воды и воздуха возможен лишь при их движении в трубах очень малого диаметра. Более вязкие жидкости, например, масла, могут двигаться ламинарно даже в трубах значительного диаметра.

Число Рейнольдса может рассматриваться как мера отношения кинетической энергии рассматриваемого элемента жидкости к работе сил вязкого трения. Действительно, кинетическая энергия элемента жидкости зависит от его объема и пропорциональна ρ₁ υ²l³ , где l — линейные размеры элемента жидкости. Работа сил вязкого трения зависит от размеров поверхности рассматриваемого элемента жидкости и пропорциональна λ l² υ. Отношение кинетической энергии элемента жидкости к работе сил вязкости будет равно:

(2.3)

Таким образом, число Рейнольдса характеризует относительную роль сил вязкости: чем оно меньше, тем большую роль играют силы вязкости в движении жидкости. Чем больше число Рейнольдса, тем больше влияние сил инерции в потоке по сравнению с силами вязкости. Опыты показывают, что одновременно с переходом ламинарного движения в турбулентное изменяется характер распределения скоростей по сечению трубы, а также характер гидравлических сопротивлений. / / На рис. 2.1а изображено распределение скоростей по сечению при ламинарном движении жидкости в трубе, имеющее параболический характер: непосредственно у стенок скорости равны нулю, а при удалении от них непрерывно и плавно возрастают, достигая максимума на оси трубы. На рис. 2.1б представлено распределение скоростей при турбулентном движении жидкости в трубе. При турбулентном движении закон распределения скоростей сложнее: в пределах большей части поперечного сечения скорости лишь незначительно меньше максимального значения (на оси), но вблизи стенок величина скорости резко падает.

а) б)

Рис. 2.1 – Распределение скоростей при ламинарном (а) и турбулентном (б)

движении жидкости

Более равномерное распределение скоростей по сечению при турбулентном движении объясняется наличием турбулентного перемешивания, осуществляемого поперечными составляющими скоростей, благодаря чему частицы с большими скоростями в центре потока и с меньшими скоростями на его периферии, непрерывно сталкиваясь, выравнивают свои скорости. У стенки турбулентное перемешивание парализуется наличием твердых границ, и поэтому там наблюдается значительно более быстрое падение скорости. В результате, ламинарный и турбулентный режим отличаются не только характером движения частиц (наличием поперечных скоростей при турбулентном движении), но и особенностями распределения скоростей по сечению и характером зависимости между потерями напора и скоростью (при ламинарном движении потери напора пропорциональны скорости в первой степени, а при турбулентном — скорости в степени, большей единицы). / /

Основные соотношения,

1 Уравнение неразрывности (сплошности). Выражает закон сохранения массы для любого объема движущейся жидкости. В переменных Эйлера уравнение имеет вид:

, (2.4)

где ρ₁ – плотность жидкости, кг/м³;

υ – ее скорость в данной точке, м/с;

υ_x, υ_y, υ_z (u, υ, ω) – проекции скорости на координатные оси.

Для несжимаемой жидкости (ρ = const) уравнение (2.4) примет вид:

или (2.5)

Для установившегося одномерного течения в трубе с площадью поперечного сечения S уравнение неразрывности дает закон постоянства расхода ρ₁ S υ = const

Распределение составляющих скорости показано на рис. 2.2.

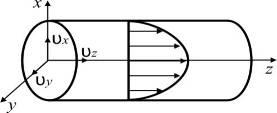
Рис. 2.2 – Распределение скоростей в системе координат (х, y, z) при ламинарном

движении

2 Уравнения Навье-Стокса. Описывают движение вязких сжимаемых жидкостей.

,

где F – напряженность поля массовых сил;

р – давление, Па.

Уравнения Навье-Стокса в проекциях на оси координат:

, (2.6)

где - проекции объемной (массовой) силы;

η – динамический коэффициент вязкости, (Н·с)/м².

Система уравнений (2.6) Навье-Стокса незамкнута, так как содержит шесть неизвестных: υ_x, υ_y, υ_z, р, ρ₁ и η. Уравнением, связывающим эти неизвестные, является уравнение неразрывности (2.5).

Для несжимаемой жидкости (ρ = const) в большинстве случаев вязкость можно считать постоянной, что позволяет упростить уравнения (2.6). После преобразований, учитывая, что , получаем

, (2.7)

где ν – кинематический коэффициент вязкости, равный η/ρ₁, м²/с.

Правые части уравнений представляют собой отнесенные к единице массы произведения массы на ускорения, а левые - сумму отнесенных к единице массы сил, в числе которых массовая сила , сила давления, выраженная по формуле (2.8), и сила внутреннего трения по формуле (9):

(2.8)

(2.9)

Если раскрыть полные ускорения , выделив в них локальную и конвективную части, то получим развернутую форму уравнений Навье-Стокса для несжимаемой жидкости:

(2.10)

Вместе с уравнением неразрывности уравнения (2.7) образуют замкнутую систему для определения функций υ_x, υ_y, υ_z и р.