2.2 Определение удельной массы радиатора
Одной из основных задач конструирования радиаторов является снижение их металлоемкости, так как изготавливаются они из дефицитных и дорогостоящих цветных металлов.
Определим физико-механические свойства материалов пластин и трубок(см таб. 1):
Таблица №1. Физико-механические свойства охлаждающих трубок и пластин
|
Параметры |
Материал |
|
|
|
|
Пластин |
Л96 |
0.407 |
8850 |
0.0002 |
|
Трубок |
Л96 |
0.408 |
8850 |
0.00015 |
Тогда
масса пластин:
,
масса
трубок:
.
С учетом этих соотношений масса остова радиатора равна:
.
Запишем
соотношение:
,
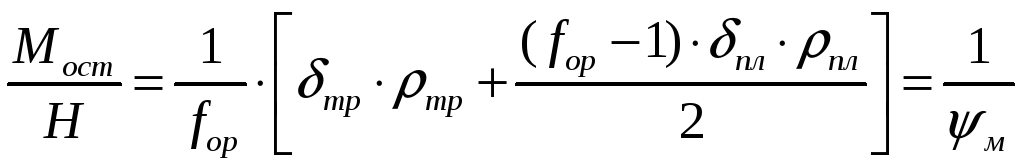Откуда
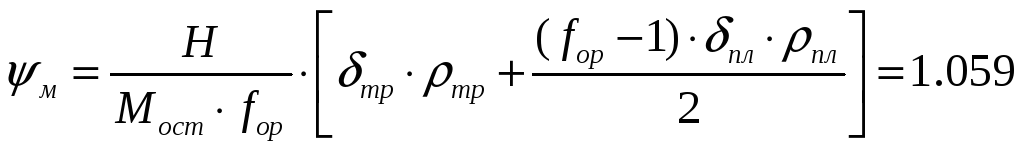- коэффициент массовой компактности
радиатора.
Отношение
- удельная масса радиатора, характеризующая
массу
его теплопередающей поверхности. Из
формулы
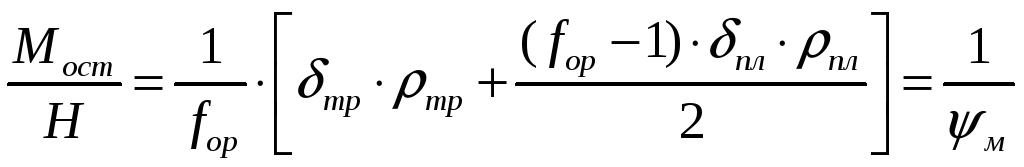видно, что удельная масса радиатора
зависит не только от плотности и толщины
используемых материалов, но и от
коэффициента оребрения. Очевидно, что
повышение коэффициента оребрения при
уменьшении расстояния между ребрами
дает возможность снизить массу
теплопередающей поверхности радиатора.
Для трубчато-пластинчатых радиаторов
средние значения удельной массы радиатора
составляют
.
В
нашем случае:
т.е. в пределах нормы.
2.3Гидравлический расчет радиатора
Гидравлический
расчет радиатора производится в следующей
последовательности. Уточняется величина
аэродинамического сопротивления
радиатора по эмпирической формуле:
.
Где
- средняя плотность воздуха при
:
,
где
- газовая постоянная воздуха.
Тогда
.
Проверка
расчета ведется по формуле:
,
где
- коэффициент гидравлического
сопротивления, определяемый по формуле:
,
-
коэффициент гидравлического потока.
Примем
.
Тогда
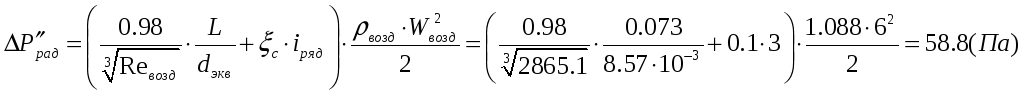
Окончательно
принимается среднее значение падения
напора воздуха в радиаторе:
.
Производится
также оценка величины гидравлического
сопротивления жидкостного тракта с
учетом того, что гидравлическое
сопротивление жидкости в радиаторе
складывается из сопротивления входа в
приемный коллектор
,
входа в трубки радиатора
,
самих трубок
,
выхода из этих трубок
и сопротивления выхода из отводящего
коллектора
Обычно
скорость жидкости в подводящей и
отводящей трубах радиатора принимают
равной
.
Перечисленные
выше сопротивления
определяются следующим образом:
,
где
- коэффициент местных потерь,
.
Тогда
.
,
где
,
.
Тогда
.
,
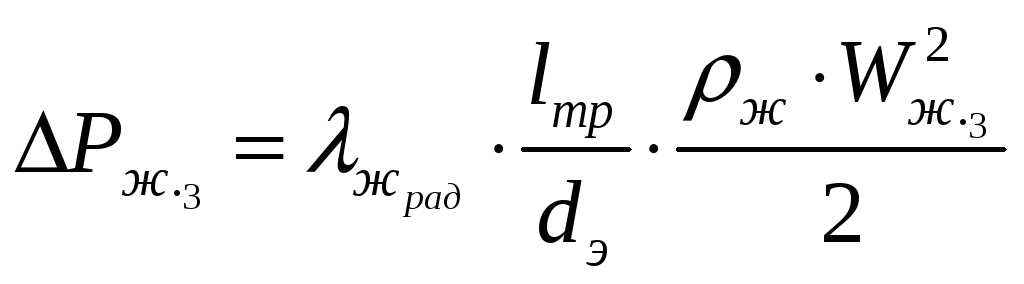где
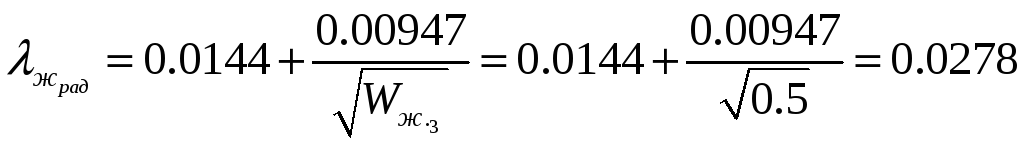- коэффициент сопротивления потерь в
трубках радиатора.
.
Тогда
.
,
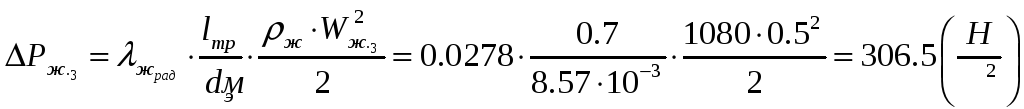где
,
.
Тогда
.
,
где
,
.
Тогда
.
Полное гидравлическое сопротивление радиатора:
.
Принято
считать, что гидравлическое сопротивление
трубопроводов и рубашек двигателя
соизмеримым с гидравлическим сопротивлением
радиатора. На основании статистических
данных – гидравлическое сопротивление
трубопроводов
,
а рубашки -
.
Тогда общее сопротивление контура охлаждающей жидкости будет равно:
.
Полученное значение общего сопротивления контура охлаждающей жидкости принимается в качестве исходного при расчете жидкостного насоса.