7. Примеры формул для расчёта отклонений от среднего (погрешностей) функций одной и нескольких переменных

Вид функции x,y,z – переменные A,a,b,c - Const	Погрешность

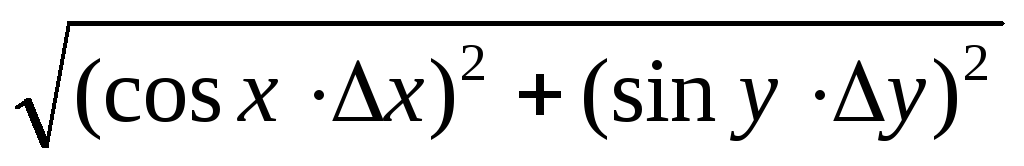
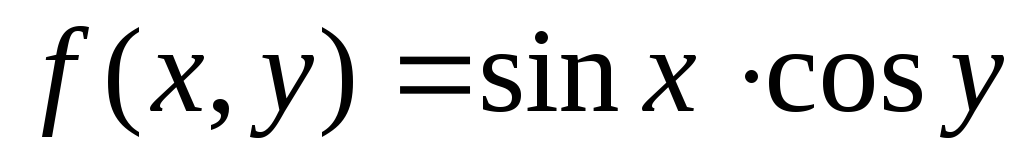
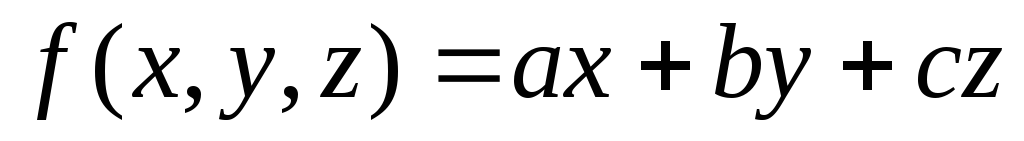
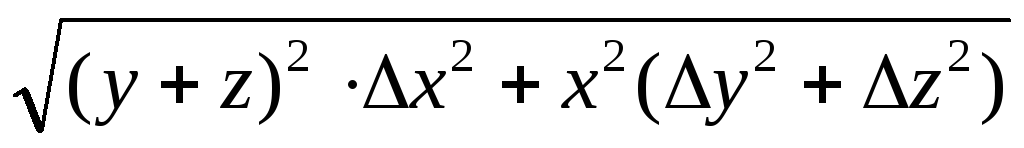
Примечание. Область существования переменных x,y,z ограничена интервалами, для которых функции и дифференциалы функций не имеют бесконечных значений.

8. Задания для самостоятельного решения

1. Найти для функций:; ; ; ; ; .

2. Измерены радиус R и масса m шара: мм; кг. Определить плотность: кг/м³ и

точность определения плотности: 100% .

3. Автомобиль проходит точку А с начальной скоростью м/с и движется дальше по прямолинейному участку шоссе с постоянным ускорением м/с² до точки В.

Расстояние от А до В равно м . Требуется найти среднюю скорость автомобиля в точке В и величину интервала , в котором будет определена скорость .

Примечание. Все отклонения (погрешности ) заданы с одинаковой доверительной вероятностью р , конкретная величина которой не существенна для данной задачи.

ПРИЛОЖЕНИЕ

Таблица 1

Коэффициенты Стьюдента

n p p pp p	0.5	0.6	0.7	0.8	0.9	0.95	0.98	0.99	0.999
2	1,0	1,38	2,0	3,1	6,3	12,7	31,8	63,7	636,6
3	0,82	1,06	1,3	1,9	2,9	4,3	7,0	9,9	31,6
4	0,77	0,98	1,3	1,6	2,4	3,2	4,5	5,8	12,9
5	0,74	0,94	1,2	1,5	2,1	2,8	3,7	4,6	8,6
6	0,73	0,92	1,2	1,5	2,0	2,6	3,4	4,0	6,9
7	0,72	0,90	1,1	1,4	1,9	2,4	3,1	3,7	6,0
8	0,71	0,90	1,1	1,4	1,9	2,4	3,0	3,5	5,4
9	0,71	0,90	1,1	1,4	1,8	2,3	2,9	3,4	5,0
10	0,70	0,88	1,1	1,4	1,8	2,3	2,8	3,3	4,8
11	0,70	0,88	1,1	1,4	1,8	2,2	2,8	3,2	4,6
12	0,70	0,87	1,1	1,4	1,8	2,2	2,7	3,1	4,5
13	0,70	0,87	1,1	1,4	1,8	2,2	2,7	3,1	4,3
14	0,69	0,87	1,1	1,4	1,8	2,2	2,7	3,0	4,2
15	0,69	0,87	1,1	1,3	1,8	2,1	2,6	3,0	4,1
20	0,69	0,87	1,1	1,3	1,7	2,1	2,5	2,9	3,9
30	0,68	0,85	1,1	1,3	1,7	2,0	2,5	2,8	3,7
40	0,68	0,85	1,1	1,3	1,7	2,0	2,4	2,7	3,6
60	0,68	0,85	1,0	1,3	1,7	2,0	2,4	2,7	3,5
120	0,68	0,85	1,0	1,3	1,7	2,0	2,4	2,6	3,4
∞	0,67	0,84	1,0	1,3	1,6	2,0	2,3	2,6	3,3

Таблица 2.