3. Два примера рекурсивных программ

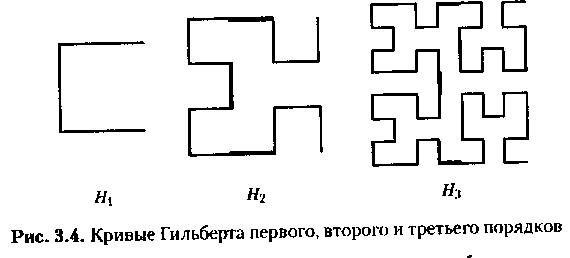
Симпатичный узор на рис. 3.3 состоит из суперпозиции пяти кривых. Эти кривые соответствуют некоторому регулярному образу и считается, что их можно нарисовать на экране дисплея или на графопостроителе под управлением какой-либо вычислительной машины. Наша задача – найти рекурсивную схему, по которой можно было бы создать программу для такого рисования. Рассматривая рис. 3.3, мы обнаруживаем, что три наложенные друг на друга кривые имеют форму, показанную на рис. 3.4; обозначим их через H₁, H₂ и H_3.. Видно, что H_i+1 получается соединением четырех экземпляров H_i вдвое меньшего размера, повернутых соответствующим образом и «стянутых» вместе тремя прямыми линиями. Заметим, что Н₁ можно считать состоящей из четырех вхождений пустой H₀, соединенных этими же тремя линиями. Кривая H_i называется кривой Гильберта i-го порядка в честь ее первооткрывателя Д. Гильберта (1891 г.).

П

оскольку каждая кривая H_i состоит из четырех вдвое меньших H_i–1, то процедура для рисования H_i будет включать четыре обращения для рисования H_i–1 соответствующим образом повернутых и уменьшенных вдвое. Для наглядности мы обозначим эти четыре части через A, В, С и D, а процедуры, рисующие соединительные прямые, будем обозначать стрелками, указывающими соответствующее направление. В этом случае появляется такая схема рекурсий (см. рис. 3.4):

П

редставим себе, что для рисования части прямой в нашем распоряжении есть процедура line, передвигающая перо в заданном направлении на заданное расстояние. Для удобства будем предполагать, что направление задается целым параметром i как 45i градусов. Если единичную длину прямой обозначить че­рез u, то с помощью рекурсивных обращений к аналогично составленным процедурам для В и D и к самой А легко написать процедуру, соответствующую схеме А:

P

Рис. 3.5. Рамка для кривых

ROCEDURE A(i: INTEGER);

BEGIN

IF i > 0 THEN

D(i-1); line{4,u);

A(i-l); line(6,u);

A(i-1); line(0,u);

B(i-1)

END

END A;

Эта процедура инициируется главной программой по одному разу для каждой из кривых Гильберта, образующих приведенный на рис. 3.4 узор. Главная программа определяет начальную точ» кривой, т. е. исходные координаты пера (Р_х и Р_у) и единичное приращение u. Заданного размера квадрат, где рисуется кривая, помещается в середине страницы (см. рис. 3.5). Величина h₀ должна удовлетворять равенству h₀ = 2^k для некоторого k  n. Эти параметры, так же как и процедура рисования прямой, находятся в модуле с названием LineDrawing. Программа рисует n кривых Гильберта – H₁,. H₂, , H_n (см. листинг 3.1 и рис. 3.4).

Кривые Гильберта

MODULE Hilbert;

FROM Terminal IMPORT Read;

FROM LineDnwing IMPORT width, height, Px, Py, clear, line;

CONST SquareSize = 512;

UNSIGNED i, x0, y0, u;

CHAR ch;

PROCEDURE A(i)

BEGIN

IF i>0 THEN

D(i-1); line(4,u); A(i-1); line(6,u);

A(i-1); line(0,u); B(i-1);

END A;

PROCEDURE B(i)

BEGIN

IF i>0 THEN

C(i-1); line(2,u); B(i-1); line(0,u);

B(i-1); line(6,u); A(i-l)

END B;

PROCEDURE C(i)

BEGIN

IF i>0 THEN

B(i-1); line(0,u); C(i-1): line(2,u);

C(i-l); line(4,u); D(i-1)

END C;

PROCEDURE D(i)

BEGIN

IF i>0 THEN

A(i-1); line(6,u); D(i-1); line(4,u);

D(i-1); line(2,u); C(i-l)

END D;

BEGIN clear;

x0 = width >> 1; y0 = height >> 1;

u=SquareSize; i=0;

DO

{

i++;

u>>1;

x0+=(u>>1); y0+=(u>>1);

Px=x0; Py=y0: A(i); Read(ch)

UNTIL (ch = 33C)||(i=6);

END Hilbert

П

одобный, но более сложный и эстетически утонченный пример приводится на рис. 3.7. Он также получен путем наложения друг на друга нескольких кривых. Первые две из них показаны на рис. 3,6. Кривая S_i называется кривой Серпинского i-го порядка. Какова же рекурсивная схема этих кривых? Попробуем в качестве основного строительного блока взять S_i, возможно, без одного ребра. Это не приведет нас к решению. Главное отличие кривой Серпинского от кривой Гильберта состоит в том, что первая замкнута (и в ней нет пересечений). Это означает, что основная рекурсивная схема должна давать разомкнутую кривую, четыре части которой соединяются линиями, не принадлежащими самому рекурсивному образу. И действительно, эти замыкающие линии представляют собой отрезки прямых в четырех внешних углах (на рис. 3.6 они выделены жирными линиями). Можно считать, что они принадлежат к непустой начальной кривой S – квадрату, «стоящему» на одном углу. Теперь легко составить рекурсивную схему. Четыре составляющих образа вновь обозначим через А, B, С, D, а связывающие линии будем рисовать явно. Обратите внимание: четыре рекурсивных образа по существу идентичны, они лишь поворачиваются на 90°.

Основной образ кривых Серпинского задается схемой

а рекурсивные составляющие (горизонтальные и вертикальные отрезки – удвоенной длины) – схемой

Если использовать те же примитивы рисования, что и в случае кривых Гильберта, то приведенные рекурсивные схемы без труда трансформируются в (прямо или косвенно) рекурсивный алгоритм.

P

ROCEDURE A(INT k);

BEGIN

IF k>0 THEN

A(k-1); line(7,h);

B(k-1); line(0,2*h);

D(k-1); lined,h); A(k-1)

END A;

Эта процедура порождается из первой строки рекурсивной схемы (3.22). Аналогично получаются и процедуры, соответствую­щие образам В, С и D. Главная программа строится по образу (3.21). Ее задача – установить начальные значения для координат рисунка и задать единичную длину линий h; это все зависит от формата бумаги (листинг 3.2). На рис. 3.7 приведен результат работы такой программы с n = 4.

Ясно, что в этих примерах рекурсия используется элегантным способом. Правильность программ легко подтверждается их структурой и формируемыми образами. Кроме того, употребление в соответствии со схемой (3.5) явного параметра для уровня гарантирует окончание работы, так как глубина рекурсии не может быть больше n. По сравнению с таким рекурсивным построением эквивалентные программы, где избегали употребления рекурсии, выглядят крайне сложными и запутанными.

Листинг 3.2. Кривые Серпинского

MODULE Sierpinski;

FROM Terminal IMPORT Read:

FROM lineDrawing IMPORT width, height, Px, Py, clear, line;

CONST SquareSize = 512;

UNSIGNED i, h, x0, y0;

CHAR ch;

PROCEDURE A(k);

BEGIN

IF k>0 THEN

A(k-1); line(7, h); B(k-1), line(0, 2*h);

D(k-1); lined, h); A(k-1)

END A;

PROCEDURE B(k);

BEGIN

IF k>0 THEN

B(k-1); line(5, h); C(k-1); line(6, 2*h);

A(k-1); line(7, h); B(k-1)

END B;

PROCEDURE C(k);

BEGIN

IF k>0 THEN

C(k-1); line(3, h): D(k-1); line(4, 2*h);

B(k-1); line(5. h); C(k-1)

END C;

PROCEDURE D(k);

BEGIN

IF k>0 THEN

D(k-1); lined, h); A(k-1); line(2, 2*h);

C(k-1); line(3, h); D(k-1)

END D;

BEGIN

clear;

i = 0; h = SquareSize>>2;

x0 = width >> 1; y0 = height >> 1 + h;

DO i++: x0-=h;

h>>1; yO+=h; Px = x0: Py = y0;

A(i): line(7, h); B(i); line(5, h):

C(i): line(3, h); D(i); line(1, h); Read(ch)

UNTIL (i = 6) || (ch = 33C);

clear

END Sierpinski.