Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ВАРИАНТЫ КОНТРОЛЬНОЙ№1 ПО МАТЕМАТИКЕ.doc

Скачиваний:

Добавлен:

05.11.2018

Размер:

3.22 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

6.3. Приложение теорем Ролля, Лагранжа, Коши. Правило Лопиталя

1. Теорема Ролля. Если функция непрерывна на отрезке , дифференцируема на интервале и , то существует хотя бы одна точка такая, что .

2. Теорема Лагранжа. Если функция непрерывна на отрезке и дифференцируема на интервале , то существует точка такая, что (формула Лагранжа).

3. Теорема Коши. Если функции и непрерывны на отрезке , дифференцируемы на интервале и , то существует точка такая, что (формула Коши).

Пример 6.8. Доказать, что уравнение имеет только один действительный корень.

Решение. Поскольку функция непрерывна и на концах отрезка принимает значение разных знаков , то по первой теореме Больцано–Коши на интервале уравнение имеет корень. Предположим, от противного, что это уравнение имеет два действительных корня .

Тогда по теореме Ролля на интервале существовала бы точка , в которой . Но при действительных . Полученное противоречие доказывает, что действительный корень – единственный.

Пример 6.9. Используя формулу Лагранжа, доказать неравен-ство .

Решение. Функция удовлетворяет условиям тео-ремы Лагранжа на любом отрезке . Поэтому . Отсюда, учитывая, что , имеем .

Пример 6.10. Написать формулу Коши и найти значение для функций на отрезке .

Решение. Все условия теоремы Коши выполнены: . Поэтому

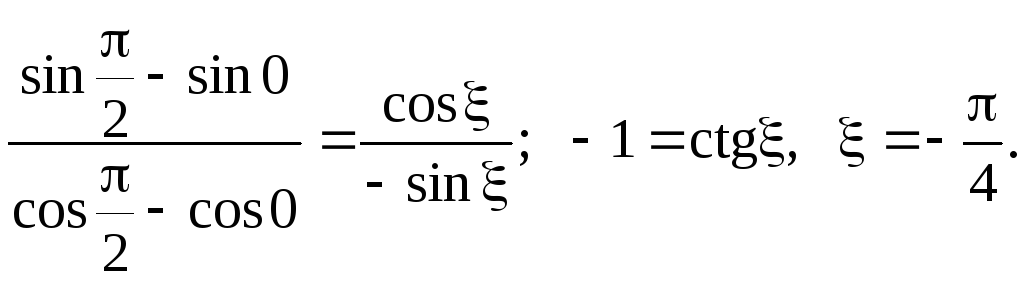
Правило Лопиталя (раскрытие неопределенностей и ).

Пусть – окрестность точки с выброшенной точкой .

Теорема. Пусть функции и дифференцируемы на ; .

Если и (или и ), то при условии, что сущест-вует предел отношения производных.

Замечания:1. Аналогичная теорема справедлива и в случае .

2. Если частное в точке также есть неопределенность вида или и производные и удовлетворяют соответствующим условиям, то можно перейти к отношению вторых производных и т.д.

3. Неопределенности вида или алгебраическими пре-образованиями функции приводятся к неопределенности вида или , и далее применяется правило Лопиталя.

4. В случае неопределенности вида , или , или следует прологарифмировать функцию и предварительно найти предел ее логарифма.

Пример 6.11.

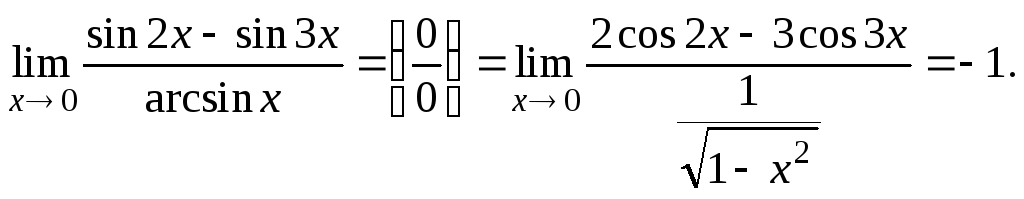
Пример 6.12.

Пример 6.13.

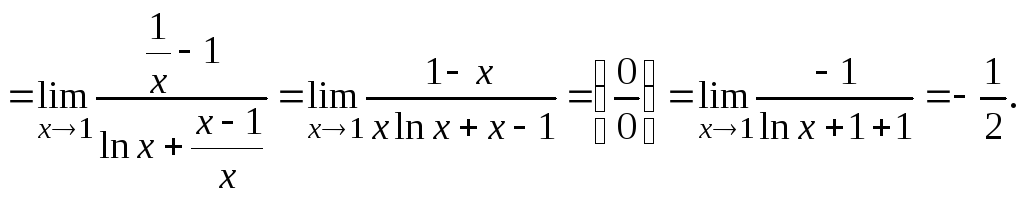
Пример 6.14. . Здесь неопределенность вида . Обозначим . Логарифмируя и применяя правило Лопиталя, получим

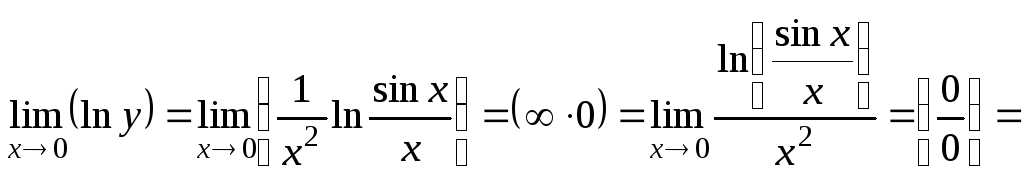
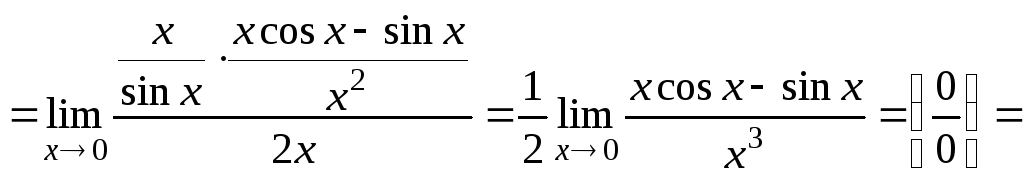
(здесь дважды использован предел ).

Поскольку , то .

6.4. Формула Тейлора и ее приложения

Если функция дифференцируема раз в окрестности точки , то для любого имеет место формула Тейлора n-го порядка

где – остаточ-ный член в форме Лагранжа.

Приведем разложения некоторых функций по формуле Тейлора при :

;

Остаточный член формулы Тейлора может быть представлен в форме Пеано: при .

Пример 6.15. Разложить многочлен по степеням двучлена

Решение. Поскольку – многочлен 4-й степени, то и формула Тейлора при имеет вид

Подставляя в эту формулу значения , получим

Пример 6.16. Написать формулу Тейлора 3-го порядка для функции в точке

Решение. Имеем

По формуле Тейлора получаем

Пример 6.17. Вывести приближенную формулу и оценить ее точность при

Решение. Запишем формулу Тейлора 4-го порядка для функ-ции в точке :

где

При имеем .

Поэтому с точностью .

Пример 6.18. Вычислить с точностью до .

Решение. Формула Тейлора для функции имеет вид

где

Полагая получим:

где

Так как то

Определим наименьшее значение n так, чтобы выполнялось неравенство .

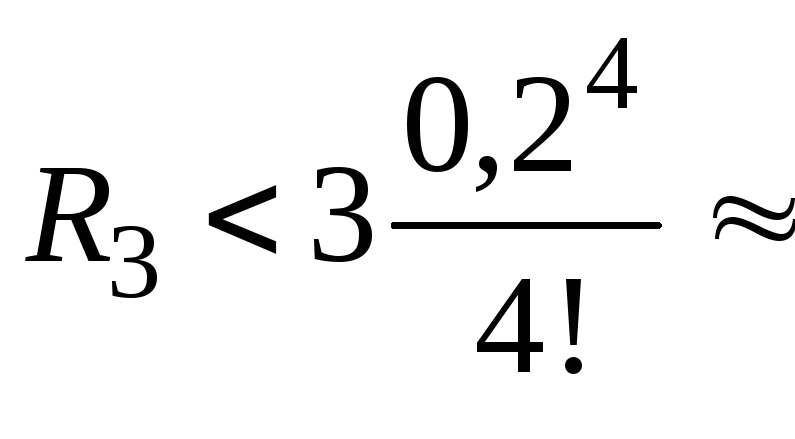
Если то , а если , то Поэтому с точностью до .

Пример 6.19. Вычислить

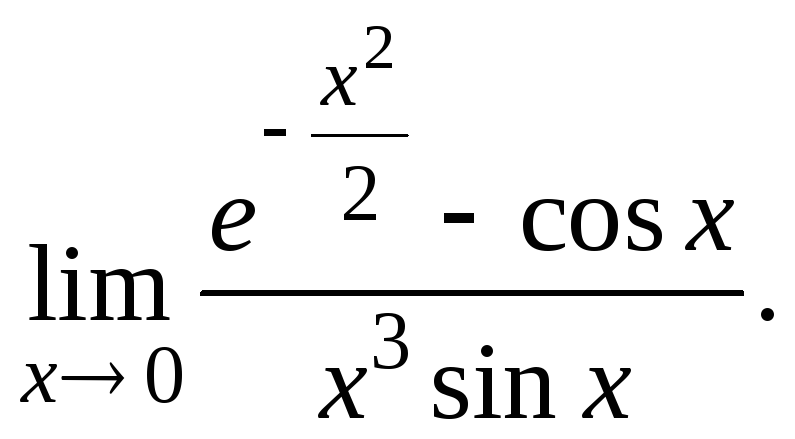
Используем формулу Тейлора с остаточными членами в форме Пеано:

Из последней формулы при получим

Искомый предел может быть переписан в виде

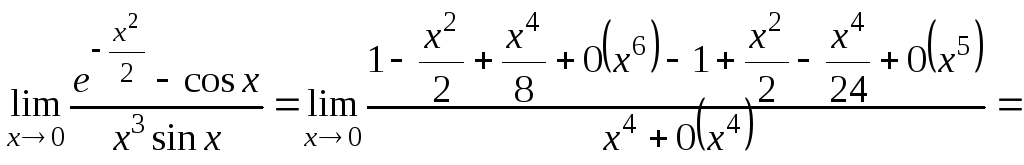
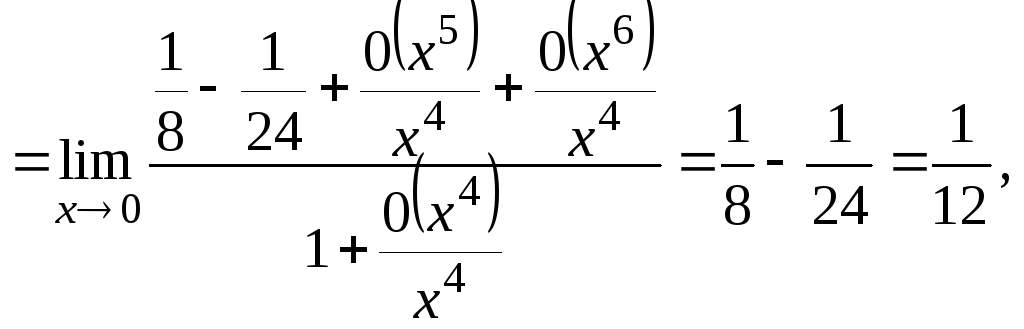
(поскольку при ).

7. ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ И ПОСТРОЕНИЯ

ИХ ГРАФИКОВ

7.1. Исследование функций на экстремум. Выпуклость

и вогнутость кривой, точки перегиба. Асимптоты

Если существует окрестность точки такая, что для всякой точки этой окрестности выполняется неравенство (или ), то точка называется точкой минимума (максимума) функции . Точки минимума и максимума функции называются ее точками экстремума.

Теорема 1 (необходимое условие экстремума). Если – точка экстремума функции , то или не существует ( – критическая точка этой функции).

Теорема 2 (первое достаточное условие экстремума). Пусть функция дифференцируема в некоторой окрестности критической точки , за исключением, быть может, самой этой точки. Если при этом в интервалах и производная имеет противоположные знаки, то – точка экст-ремума, причем если при и при , то – точка максимума. Если же при и сохраняет знак, то точка не является точкой экстремума.

Теорема 3 (второе достаточное условие экстремума). Пусть дважды дифференцируема и . Если , то – точка максимума функции , если , то – точка минимума. Если же , то требуются дополнительные исследования.

Если на интервале (a; b) всякая касательная располагается выше (ниже) дуги кривой, то график дифференцируемой функции на этом интервале называется выпуклым (вогнутым).

Если на интервале (a; b), то график функции является вогнутым на этом интервале; если же , то график функции – выпуклый на (a; b).

Точка , при переходе через которую направление вы-пуклости графика функции меняется на противоположное, называется точкой перегиба.

Теорема 4 (необходимое условие точки перегиба). Если – абсцисса точки перегиба графика функции , то или не существует.

Теорема 5 (достаточное условие точки перегиба). Пусть функция дважды дифференцируема в некоторой окрестности точки , в которой или не существует. Если при этом в интервалах и вторая производная имеет противоположные знаки, то – точка перегиба.

Прямая l называется асимптотой графика функции , если расстояние от точки М(x, f(x)) графика функции до прямой l стремится к нулю при неограниченном удалении точки М от начала координат.

Для существования вертикальной асимптоты х = а необходимо и достаточно, чтобы хотя бы один из односторонних пределов был равен бесконечности.

Для существования наклонной асимптоты необходимо и достаточно существование двух пределов

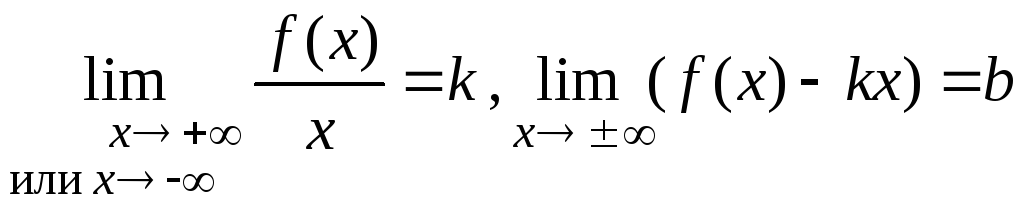Пример 7.1. Для функции найти интервалы возрастания и убывания и точки экстремума.

Решение. Находя производную и приравнивая ее нулю, получаем и (при х = 0 не существует). Эти точки разбивают область определения функции на интервалы монотонности. Результаты исследования удобно представить в виде таблицы.

х		–1	(–1; 0)	0	(0; 1)	1	()
	+	0	–	Не сущ.	+	0	–
		1		Не сущ.		1	

Следовательно, – интервалы возрастания функции; – интервалы убывания функции; – точки максимума. Точек минимума нет.

Пример 7.2. Для графика функции найти интервалы выпуклости и вогнутости и точки перегиба.

Решение. Находим вторую производную . Критическими точками второй производной являются точки 0 и 6 ( в этих точках не существует). Они разбивают область определения функции на три интервала, на которых сохраняется направление выпуклости или вогнутости. Результаты исследования удобно представить в виде таблицы.