
- •Лекция 2 Определение вероятностей сложных событий
- •От простых событий к сложному
- •Вероятностная модель испытаний Бернулли
- •Теорема Бернулли
- •Формула Бернулли
- •Обобщенная формула Бернулли
- •Практическое нахождение достаточного числа повторений
- •Локальная теорема Лапласа
- •Интегральная теорема Лапласа
- •Условие для необходимого числа испытаний
- •Вычисления функции Лапласа в среде matlab
- •Решение обратной задачи
- •Формула Пуассона
- •Оценка вероятности по частоте успехов в испытаниях Бернулли
- •Применение нормального приближения
- •Оценка вероятности по частоте маловероятных событий в испытаниях Бернулли
- •Универсальный метод оценки вероятности по частоте
- •Построение кривой чувствительности
- •Построение кривой чувствительности при ограниченном объеме статистики
- •Вероятность нескольких попаданий в серийной стрельбе
- •Повторение опытов в меняющихся условиях
- •Универсальная электронная формула для независимых испытаний
- •Пример применения универсальной электронной формулы RptTrial
- •Ординарные потоки и поля событий
- •Ординарные потоки событий
- •Вероятность событий в простейшем пуассоновский потоке
- •Пуассоновский поток событий
- •Простейшее пуассоновское поле событий
- •Иллюстрация статистически равномерного распределения
- •Пуассоновское поле событий
- •Координатный закон поражения
- •Кзп в однородном поле
- •Кзп в неоднородном поле
- •Статистическое моделирование пуассоновского поля
- •БэсПиБп.2. Случайные события. Повторение опытов 16
Лекция 2 Определение вероятностей сложных событий
От простых событий к сложному
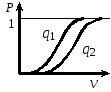 Рис.
2.1. Кривые вероятностей пробития
Рис.
2.1. Кривые вероятностей пробития
Применение той или иной вероятностной модели сложных событий должно быть согласовано с условиями реального опыта. Модели, предполагающие независимость простых событий, сильно упрощают вычисления, но могут привести к ошибочным выводам. Если события поражения отдельного УА каждым попавшим в него осколком еще можно считать независимыми, то каждое попадание снаряда в трудноуязвимую цель повышает вероятность поражения в следующих попаданиях из-за накопления ущерба. В таких случаях статистическая вероятность поражения цели одним попавшим снарядом r1 не вполне характеризует уязвимость цели. Приходится в статистических испытаниях определять закон поражения – условную вероятность поражения цели при m попаданиях G(m) = P(A/m), m = 1, 2, … с учетом накопления ущерба: G(m) > 1– (1 – r1)m. Чтобы применить формулу полной вероятности (1.17) к событию поражения одиночной цели в n выстрелах, нужны также вероятности гипотез Am, n (m попаданий в n выстрелах). В некоторых случаях вероятности pm,n = P(Am, n) можно определить по вероятности попадания в одном выстреле p1, используя закономерности повторяющихся в одинаковых условиях независимых опытов, но реальная стрельба (очередью, залпом) не вполне соответствует такой вероятностной модели. Тем не менее, модель независимых испытаний в неизменных условиях дает фундаментальные соотношения, необходимые для разумного применения статистических методов при определении вероятностей простых событий.
