БАЛАШОВСКОЕ ВЫСШЕЕ ВОЕННОЕ АВИАЦИОННОЕ УЧИЛИЩЕ
им. главного маршала авиации А.А. НОВИКОВА
ОСНОВЫ ВОЗДУШНОЙ НАВИГАЦИИ
С ЗАДАЧАМИ
(Учебное пособие)
1997 год
ПОКИДКИН ЮРИЙ МИХАЙЛОВИЧ
ОСНОВЫ ВОЗДУШНОЙ НАВИГАЦИИ С ЗАДАЧАМИ
(Учебное пособие)
1997 год
Р А З Д Е Л 1.
Краткие сведения из математики
а. Алгебра
Формулы сокращенного умножения многочленов.
1.
2.
3.
4.
5.
Правила действий со степенями.
1.
5.
2.
6.
3.
7.
4.
8.
9.
при любом
Б. Геометрия
Площадь треугольника
,
где:
— полупериметр
В прямоугольном треугольнике сторона, лежащая против угла 90° — гипотенуза; две другие стороны — катеты.
Квадрат
гипотенузы равен сумме квадратов
катетов, т.е.
Площадь
треугольника равна половине основания,
умноженного на высоту, т.е.
.
Окружность.
Длина
окружности:
,
где p = 3,14
Площадь круга S = pr2
длина
дуги
:
(угол a
выражен в градусах ),
r
a
(угол a
выражен в радианах)
В. Тригонометрия
Радианное измерение углов
Радиан есть угол, длина дуги которого равна радиусу.
1
радиан =
градусов = 57°17¢44¢¢
Тригонометрические функции
1. Тригонометрические функции угла a определяются при помощи тригонометрического круга. Положительные углы откладываются от неподвижного радиуса АО против часовой стрелки, отрицательные по часовой стрелке
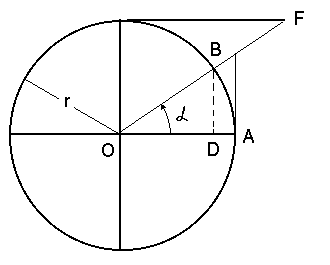
синус
sina=
котангенс ctga=
косинус
cosa=
секанс seca=
тангенс
tga=
косеканс coseca
=
В зависимости от четверти, в которой лежит угол a, записанные отношения берутся со знаком (+) плюс или (-) минус. Все тригонометрические функции углов 1 четверти положительны.
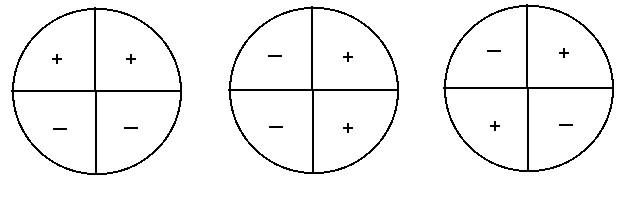
1 четверть 0°£ a £ 90°
2 четверть 90°£ a £ 180°
3 четверть 180°£ a £ 270°
4 четверть 270°£ a £ 360°
2. Числовые значения тригонометрических функций некоторых углов.
|
Функция |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
Функция |
|
|
0 |
|
|
|
|
p |
|
2 p |
|
|
sin |
0 |
|
|
|
1 |
0 |
-1 |
0 |
sin |
|
cos |
1 |
|
|
|
0 |
-1 |
0 |
1 |
cos |
|
tg |
0 |
|
1 |
|
± ¥ |
0 |
± ¥ |
0 |
tg |
|
ctg |
± ¥ |
|
1 |
|
0 |
± ¥ |
0 |
± ¥ |
ctg |
|
sec |
1 |
|
|
2 |
± ¥ |
-1 |
± ¥ |
1 |
sec |
|
cosec |
± ¥ |
2 |
|
|
1 |
± ¥ |
1 |
± ¥ |
cosec |
3. Тригонометрические функции любых углов могут быть сведены с помощью формул приведения к функциям острых углов, а значения последних берутся из таблиц (или определяются по НЛ- 10).
4. Формулы приведения.
|
Функция |
|
|
У Г ОЛ |
|
|
|
|
Функция |
|
|
90 - a |
90 + a |
180 - a |
180 + a |
270 - a |
270 + a |
360 - a |
|
|
sin |
cos a |
cos a |
sin a |
- sin a |
- cos a |
- cos a |
- sin a |
sin |
|
cos |
sin a |
- sin a |
- cos a |
- cos a |
- sin a |
sin a |
cos a |
cos |
|
tg |
ctg a |
- ctg a |
- tg a |
tg a |
ctg a |
- ctg a |
tg a |
tg |
|
ctg |
tg a |
- tg a |
- ctg a |
ctg a |
tg a |
- tg a |
- ctg a |
ctg |
|
sec |
cosec a |
- cosec a |
- sec a |
- sec a |
- cosec a |
cosec a |
sec a |
sec |
|
cosec |
sec a |
sec a |
cosec a |
- cosec a |
- sec a |
- sec a |
- cosec a |
cosec |
5. sin (- a ) = - sin a cos (- a ) = cos a
tg(- a ) = - tg a ctg (- a ) = - ctg a
sec (- a ) = sec a cosec (- a ) = - cosec a
Основные формулы тригонометрии
1. sin 2 a + cos 2 a = 1 5. cos a × sec a =1
2.
tg a
=
6. tg a
×
ctg a
=1
3.
ctg a
=
7. sec2
a
=
tg2
a
+1
4. sin a × cosec a = 1 8. cosec 2 a = ctg 2 a +1
Функции суммы и разности двух углов
sin (a ± b ) = sin a × cos b ± cos a × sin b
cos
(a
±
b
) = cos a
×
cos b
sin a
×
sin b
tg
(a
±
b
) =
ctg
(a
±
b
) =
Функции двойного угла
sin 2a = 2 sin a × cos a cos 2 a = cos 2 a - sin 2 a
tg
2a
=
ctg 2a
=
sin
2a
=
cos 2 a
=
Функции половинного угла
sin
cos
tg
ctg
Знак
перед радикалом берется в зависимости
от той четверти, в которой лежит угол
.