2.Порядок выполнения работы

1. Включить осциллограф. Получить на экране четкое изображение развертки луча (горизонтальная линия).

2. Переключатель режимов работы поставить в положение “А”. Подать на “вход А” переменное напряжение определенной частоты от первого генератора и получить на экране четкую картину гармонических колебаний. Частоту колебаний задает преподаватель.

3. Переключатель режимов работы поставить в положение “Б”. Подать на “вход Б” от второго звукового генератора переменное напряжение примерно такой же частоты и амплитуды, т.е. получить на экране изображение примерно такой же синусоиды.

4. Переключатель режимов работы поставить в положение “А+Б”. На экране должна появиться картина биений. Измерить на экране осциллографа расстояние l между двумя соседними минимумами и определить период биений Т:

T = kl, где k – положение переключателя “длительность развертки”.

5. Вычислить частоту биений .

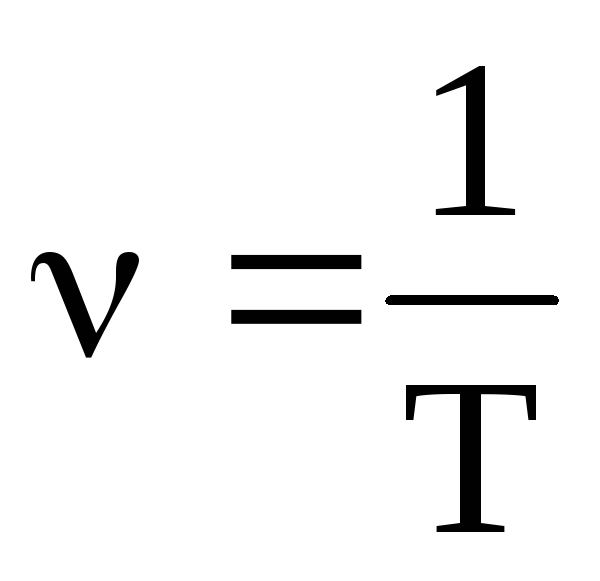6. Определить частоту колебаний второго звукового генератора по формул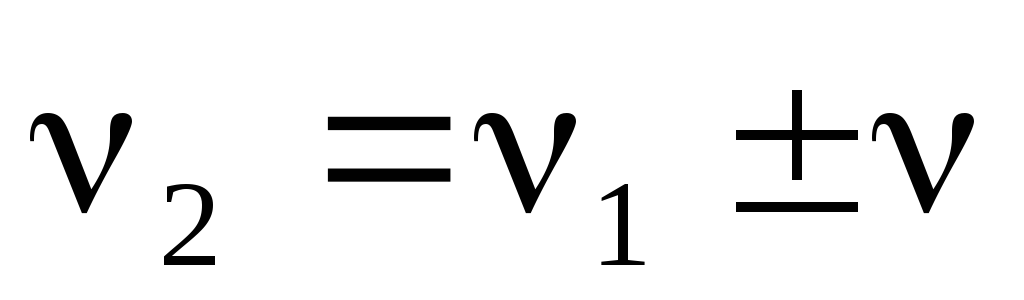е , где 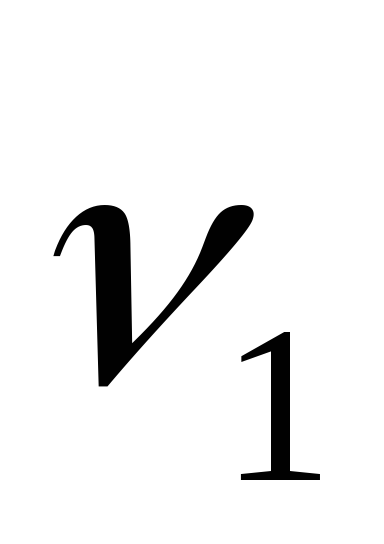- частота колебаний первого генератора, и выбрать одно из двух полученных значений, проанализировав картину колебаний на “входе А” и на “входе Б”.

7. Вычислить абсолютную и относительную погрешности измерений.

3.Контрольные Вопросы

1. Каким образом можно представить гармоническое колебание в виде вектора?

2. Что получится в результате сложения двух одинаково направленных колебаний одинаковой частоты?

3. В каком случае возникают биения? Чему равна их частота?

4. Какие фигуры смогут получиться в результате сложения двух взаимно перпендикулярных колебаний одинаковой частоты?

5. Как при помощи фигур Лиссажу определить частоту неизвестных колебаний?

лабораторная работа № 5.2

Сложение взаимно перпендикулярных колебаний

Цель работы: определить частоты колебаний методом фигур Лиссажу.

Приборы и принадлежности: электронный осциллограф, два генератора звуковой частоты, соединительные провода и кабели.

1.Вывод рабочих формул и описание установки

Рассмотрим частицу, совершающую гармонические колебания в двух перпендикулярных направлениях, вдоль осей х и у. Такие два линейных колебательных движения можно записать в виде:

.

Результирующая траектория движения в плоскости XY зависит от соотношения частот, амплитуд и фаз этих колебаний. Наиболее просто проанализировать это движение в случае равных частот: .

Тогда ,

где начальная фаза _Х – выбрана равной нулю, что всегда можно сделать, сдвинув начало отсчета времени.

Рассмотрим несколько конкретных случаев при различных величинах .

При =0 легко получаем:

, или .

Это есть уравнение прямой, проходящей через начало координат. Необходимо только учесть, что области X и Y ограничены значениями соответственно. В итоге получается отрезок прямой (рис.1).

При =2 исходные уравнения могут быть записаны в виде: .

В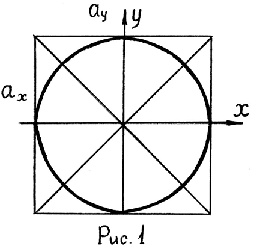озводя их в квадрат и складывая, получим уравнение траектории: .

Это - уравнение эллипса с полуосями a_X, a_Y . При a_X = a_Y эллипс превращается в окружность (рис.1).

При : . В итоге опять получается отрезок прямой (рис.1).

При других значениях сдвига фаз траектория точки представляет собой эллипс, полуоси которого повернуты на некоторый угол относительно осей х и у, но по-прежнему вписаны в прямоугольник 2a_X,, 2a_Y.

Когда частоты у двух колебаний разные, движение может быть очень сложным. В общем случае траектория оказывается даже не замкнутой, и движение, таким образом, не является периодическим.

Однако, если отношение частот равно рациональному числу, т.е. может быть представлена в виде отношения двух натуральных чисел: , то траектория оказывается замкнутой и движение является периодическим. Такого типа траектории называют фигурами Лиссажу (рис.2).

Ц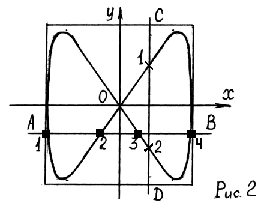енность фигур Лиссажу заключается в том, что по их форме и известной частоте одного из складываемых колебаний можно определить частоту другого колебания.

Фигура Лиссажу пересекает любую прямую, параллельную оси О_Х, n_Х раз, а прямую параллельную оси О_У, n_У раз. Эти прямые, конечно, должны проходить внутри прямоугольника, ограничивающего фигуру Лиссажу.

Отсюда вытекает правило для нахождения искомой частоты: через фигуру Лиссажу необходимо провести две прямые, параллельные осям х и у, подсчитать число точек пересечения этих прямых с фигурой, т.е. n_Х и n_У, и вычислить неизвестную частоту по формуле: .

Если прямая проходит через точку пересечения ветвей фигуры, то такую точку считают дважды.

На рис.2 показана одна из простейших фигур Лиссажу, получающаяся при отношении частот . Цифрами отмечены точки пересечения фигуры со вспомогательными прямыми АВ и DС.

Наблюдение фигур Лиссажу при разных соотношениях частот исследуемых колебаний удобно проводить осциллографическим методом. Суть метода состоит в том, что на горизонтально отклоняющие пластины осциллографа «вход X» подают колебание известной частоты _X , а на вертикально отклоняющие пластины «вход Y» - колебания с неизвестной частотой _Y. Под воздействием этих двух взаимно перпендикулярных колебаний электронный луч при соответствующем соотношении частот описывает на экране осциллографа фигуру Лиссажу.