3.Контрольные вопросы

1. Какие колебания называются вынужденными? Напишите дифференциальное уравнение этих колебаний.

2. В чем заключается явление резонанса? Как найти резонансную частоту?

3. Что такое переменный ток? Сформулируйте закон Ома для цепей переменного тока. Чем отличается этот закон от закона Ома для цепей постоянного тока?

4. Объясните сущность метода векторных диаграмм.

лабораторная работа № 5.1

Определение частоты биений

Цель работы: экспериментальное исследование явления сложения гармонических колебаний одного направления.

Приборы и принадлежности: двухлучевой осциллограф, два генератора колебаний звуковой частоты, соединительные кабели.

1.Вывод рабочих формул и описание установки

Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты:

X = X₁ + X₂ = a₁cos(ωt + α₁) + a₂cos(ωt + α₂).

Э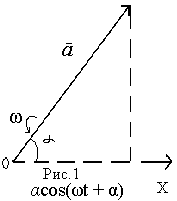ту операцию удобно выполнить, воспользовавшись графическим методом изображения колебаний.

Метод основан на том, что величину можно рассматривать как проекцию на горизонтальную ось радиус-вектора, имеющего длину a и образующего с осью угол (t+). Для этого он должен вращаться вокруг начала координат с угловой скоростью , причем начальное значение угла поворота (при t=0) должно быть равно  (рис.1). Таким образом, гармоническое колебание с амплитудой a и начальной фазой  будем изображать вектором с длиной a и образующим с осью х углом .

В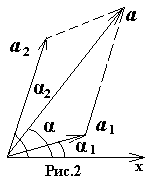 этом случае сложение колебаний одинаковой частоты заменяется сложением векторов, изображающих эти колебания (рис.2). Поскольку частота колебаний, а значит, и угловая скорость вращения векторов одинакова, то взаимное расположение векторов и на рис.2 не изменяется при их вращении. Это значит, что сумма двух колебаний одинаковой частоты представляет собой колебание этой же частоты, амплитуда которого дается модулем вектора , начальная фаза – углом, который образует этот вектор с осью х.

Из рис.2 с помощью простых геометрических соображений можно получить явные выражения для амплитуды и начальной фазы результирующего колебания :

; .

Специальный интерес представляет сложение двух колебаний с близкими частотами, такими, что разность

мала по сравнению с ₁ и ₂. Обозначим: ₁=. Тогда ₂=+, где ₁, ₂.

В этом случае вектор a₂ на рис.2 будет опережать в своем вращении вектор a₁ и длина результирующего вектора будет изменяться во времени от a_max = a₁+ a₂, когда направлены в одну сторону

до a_min = a₁ - a₂, когда направлены в противоположные стороны.

Частота этих изменений равна разности частот исходных колебаний . Следовательно, результирующее колебание будет происходить с частотой , а его амплитуда будет медленно изменяться с частотой  в указанных пределах.

Явление периодического изменения результирующей амплитуды при наложении колебаний с близкими частотами называют биением, а величина  называется частотой биений. На рис.3 изображены биения при a₁ = a₂.

Уравнение биений, получающихся в результате сложения колебаний

,

может быть записано в виде:

.

Следует иметь в виду, что амплитуда колебаний: - есть периодическая функция с частотой, в 2 раза превышающей частоту выражения, стоящего под знаком модуля.

Наблюдение биений удобно производить с помощью электронного осциллографа, имеющего два входа по оси y. Суть метода заключается в том, что на “вход А” осциллографа подают переменное напряжение с частотой υ₁, а на “вход Б” с частотой υ₂ от различных источников. В результате сложения этих колебаний на экране осцилографа можно наблюдать возникающие биения.

Для определения периода биений необходимо измерить на экране осциллографа расстояние l между соседними минимумами и вычислить период по формуле T = kl, где k – положение переключателя “длительность развертки”.