
- •7. Вычислить выражения:
- •1. Вычислить:
- •Задание № 4-2.
- •3. Вычислить определители:
- •Задание 6-1.
- •Задание № 7-1.
- •Задание № 8-5.
- •Задание 9-3.
- •2.Вычислить выражения:
- •Ответы.
- •Задание 102.
- •Ответы.
- •Задание № 13 4.
- •Ответы.
- •Задание № 142.
- •Ответы.
- •Задание № 155.
- •Ответы .
- •Задание № 16-4.
- •Ответы.
Задание 9-3.
1.Перемножить матрицы:
а)  б)
б)  в)
в) 
г) 
2.Вычислить выражения:
а)
 б)
б)  в) f(x) = x3
2x2 +
1, х =
в) f(x) = x3
2x2 +
1, х =  .
.
3.Решить
уравнения: а) ![]() б)
б) 
4.Найти
обратную матрицу к матрице: а)
![]() б)
б)  в)
в) 
5.Найти
все матрицы, коммутативные с матрицей:
А = ![]()
6.Найти общую и фундаментальную системы решений систем уравнений:
а) х1 х3 + х5 = 0, б) х1 + х2 + х3 + х4 = 0,
х2 х4 + х6 = 0, ix1 + (1 + i)x4 = 0,
х1 х2 + х5 х6 = 0, (1 + i)x2 + (1 i)x3 = 0.
х2 х3 + х6 = 0,
х1 х4 + х5 = 0,
Ответы.
1а.
 2а.
2а.  4a.
4a.
![]()
1б.
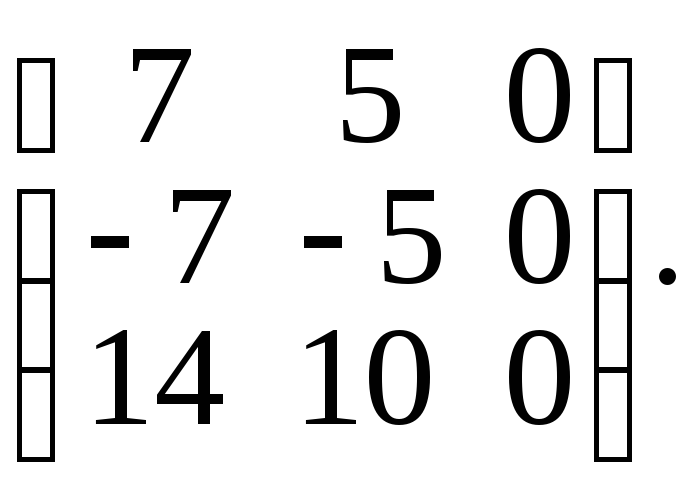 2б.
2б. ![]() 4б.
4б.

1в.
 2в.
2в.
 4в.
4в.
1г.
 3а.
3а.
![]() 3б.
X =
3б.
X =

5.

![]()
6а. ФСР: (1, 1, 1, 1, 0, 0); (-1, 0, 0, 0, 1, 0); (0, 1, 0, 0, 0, 1);
общ.
реш.:
![]()
6б. ФСР: (22i, 1+i, 1+i, 2); общ. реш.: С(22i, 1+i, 1+i, 2).
Задание 102.
1.Выполнить деление с остатком многочленов f(x) на g(x):
а) f(x) = x3 3x2 x 1, g(x) = 3x2 2x + 1;
б) f(x) = 2x5 5x3 + 8x, g(x) = x + 3.
2.При каком условии полином х4 + px2 + q делится на полином вида х2 + mx + 1?
3.Подобрать такие многочлены u(x) и v(x), что f(x)u(x) + g(x)v(x) = 1:
f(x) = x4 x3 4x2 + 4x + 1, g(x) = x2 x 1.
4.Найти наибольший общий делитель многочленов:
а) х6 + 2х4 4х3 3х2 + 8х 5 и х5 + х2 х + 1,
б) х4 4х3 + 1 и х3 3х2 + 1.
5.Найти наибольший общий делитель полинома и его производной: f(x)=(x1)3(x+1)2(x3).
6.Пользуясь алгоритмом Евклида, подобрать полиномы М1(х) и
М2(х) так, чтобы f1(x)M2(x) + f2(x)M1(x) = (x), где (x) наибольший общий делитель f1(x) и f2(x): f1(x) = x5 + 3x4 + x3 + x2 + 3x + 1,
f2(x) = x4 + 2x3 + x + 2 .
Ответы .
1а. 1/9(3x7), 1/9(26x+2). 4a. х3 x + 1.
1б.
(2x4
6x3 +
13x2
39x + 4б. x2
2![]() x
1.
x
1.
+ 125)(x + 3) 375. 5. (x1)2 (x + 1).
2. 1) q = p 1, m=0, 6. f1(x) + (x + 1)f2(x) = x3 + 1.
2)
q = 1, m = ![]() .
.
3. U(x) = x 1, V(x) = x3 + x2 3x 2.
Задание № 113
Разложить на неприводимые множители над полем С или полем
вещественных чисел многочлены:
1. х5 10х3 20х2 15х 4, 2. х4 + 4х3 + 4х2 + 1,
3. х4 ах2 + 1, х < 2, 4. x2n + хn + 1.
Ответы .
1. (x+1)4(x4).

3.
(x2
x![]() +
1)(x2
+
x
+
1)(x2
+
x![]() + 1).
+ 1).
4. ![]() x2
2xсos
x2
2xсos![]() + 1).
+ 1).
Задание № 121.
1.Пользуясь схемой Горнера, разложить полином f(x) по степеням х х0:
а) f(x) = x4 + 2x3 3x2 4x + 1,
б) f(x) = x4 2x3 + 4x2 6x + 8, x0 = 2.
2.Отделить кратные множители полиномов:
-
f(x) = x6 6x4 4x3 + 9x2 + 12x + 4,
-
f(x) = x7 3x6 + 5x5 7x4 + 7x3 5x2 + 3x 1.
3.Построить полином наименьшей степени по данной таблице значений:
 x
0 1 2 3 4
x
0 1 2 3 4
f(x) 1 2 3 4 6.
