
- •7. Вычислить выражения:
- •Вычислить:
- •Задание № 4-1.
- •Задание 5-2.
- •3. Вычислить определители:
- •Задание 6-4.
- •Задание № 73.
- •Задание № 8-4.
- •Задание 9-2.
- •2.Вычислить выражения:
- •Задание 103.
- •Ответы .
- •Задание № 114
- •Ответы .
- •Задание № 123.
- •Ответы.
- •Задание № 13 5.
- •Ответы.
- •Задание № 141.
- •Ответы.
- •Задание № 152.
- •Ответы .
- •Задание № 16-1.
- •Ответы.
Задание 9-2.
1.Перемножить матрицы:
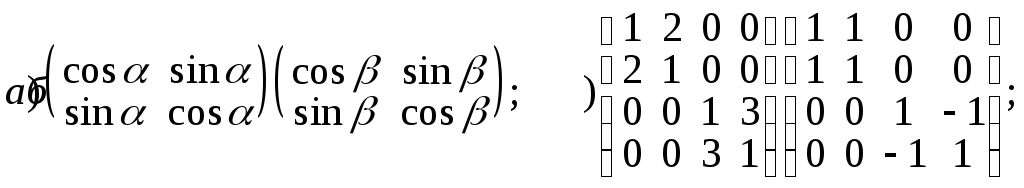
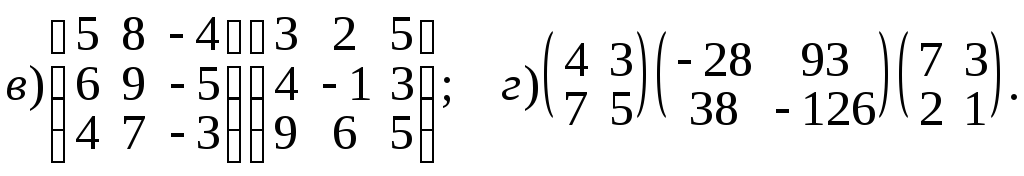
2.Вычислить выражения:
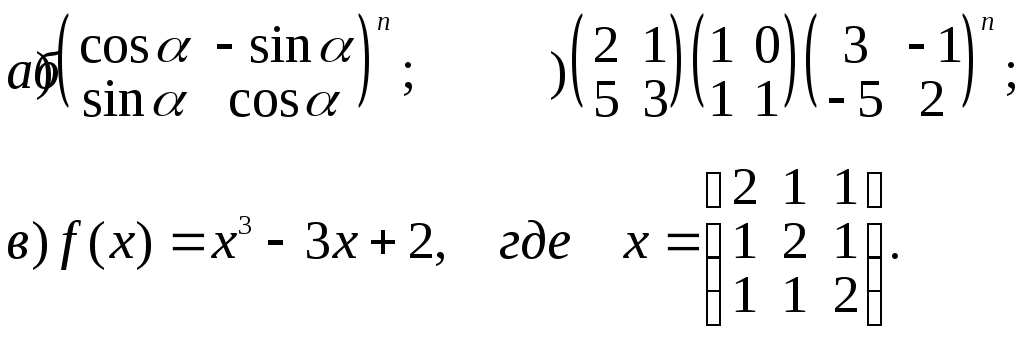
3.Решить
уравнения: а) ![]() б)
б)![]()
4.Найти
обратную матрицу к матрице: а)![]() б)
б) 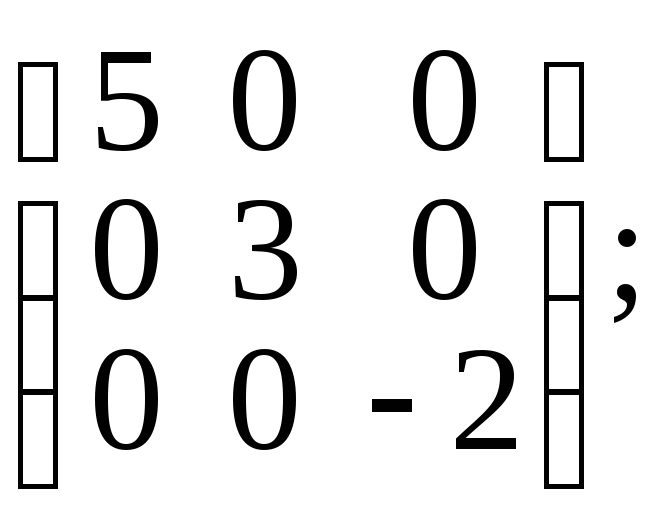 в)
в) 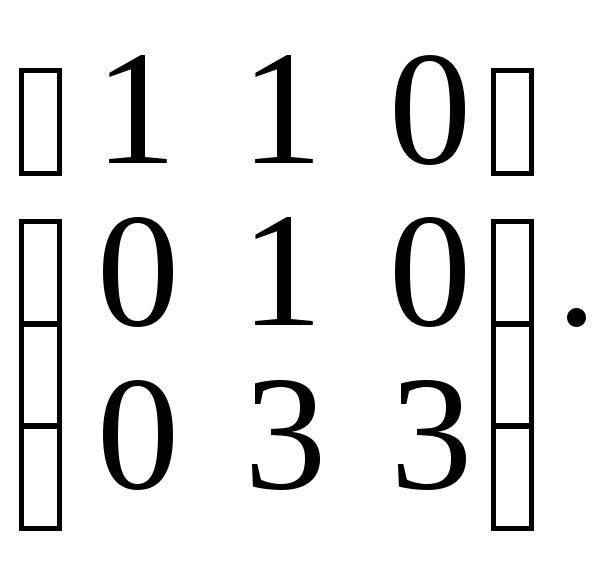
5.Найти
все матрицы, коммутативные с матрицей:
А = 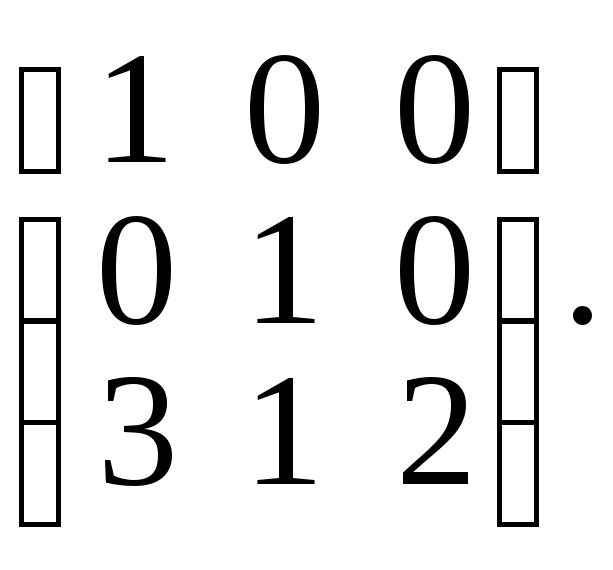
6.Найти общее решение и фундаментальную систему решений систем уравнений:
а) х1 х3 = 0, б) х1 + ix2 + x3 + x4 = 0,
х2 х4 = 0, х1 x2 + ix3 + 2x4 = 0,
х1 + х3 х5 = 0, (1 i)х1 + (1 + i)x2 + (1 i)x3 = 0.
х2 + х4 х6 = 0,
х3 + х5 = 0,
х4 + х6 = 0. Ответы.
1a.
![]() 2а.
2а. ![]() 4а.
4а.
![]()
1б.
 2б.
2б. ![]() 4б.
4б. 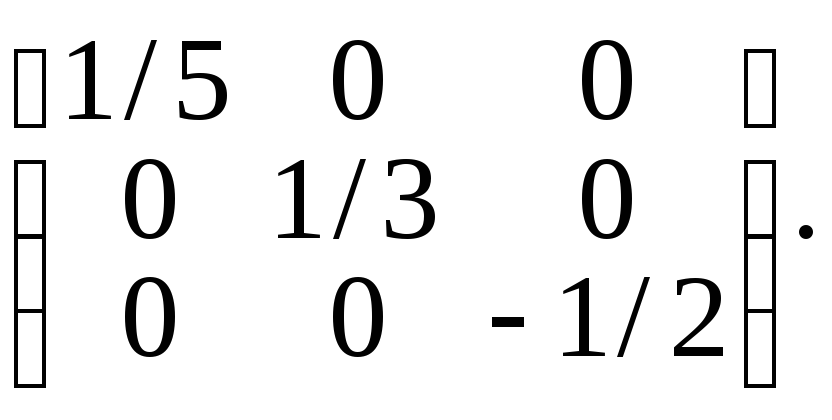
1в.
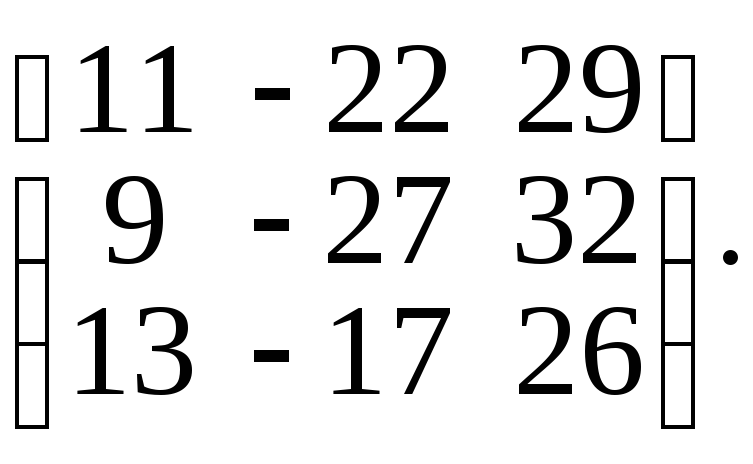 2в
2в .
4в.
.
4в.
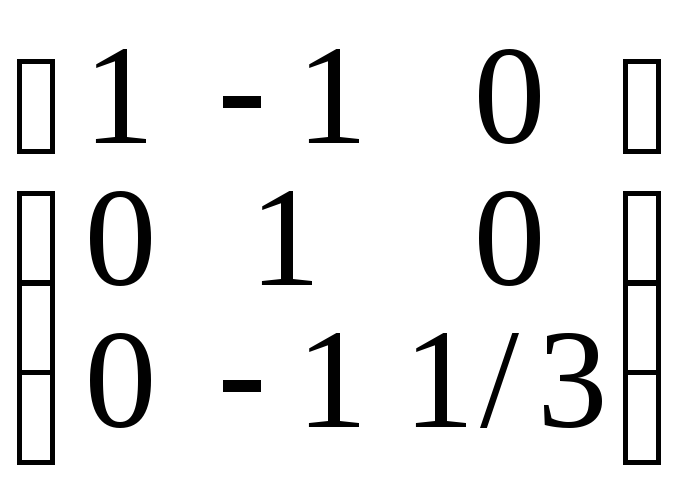 .
.
1г.
![]() .
3а.
.
3а.
![]() 3б. X =
3б. X =
![]() 5.
5.
![]() (x
y)E + yA.
(x
y)E + yA.
6a. Только нулевое решение.
6б. ФСР: (0, i, 1, 0), Общ. реш. x1 = x4 = 0, x2 = iС, x3 = С.
Задание 103.
1.Выполнить деление с остатком многочленов f(x) и g(x):
а) f(x) = x4 2x3 + 4x2 6x + 8, g(x) = (x 1);
б) f(x) = 4x3 + x2, g(x) = x + 1 + i .
2.Подобрать такие многочлены U(x), V(x), что f(x)U(x) + g(x)V(x) = 1:
a) f(x) = x4 4x3 + 1, g(x) = x3 3x2 + 1;
б) f(x) = x5 5x4 2x3 + 12x2 2x + 12, g(x) = x3 5x2 3x + 17.
3.Найти наибольший общий делитель многочленов:
а) x5 + 3x2 2x + 2 и x6 + x5 + x4 3x2 + 2x 6;
б) x5 + x4 x3 3x2 3x 1 и x4 2x3 x2 2x + 1.
4.Найти наибольший общий делитель полинома и его производной f(x)=(x 1)(x2 1)(x3 1)(x4 1).
5.Пользуясь алгоритмом Евклида, подобрать полиномы М1(х) и
М2(х) так, чтобы f1 (x)M2(x) + f2(x)M1(x) = (x), где (x) наибольший общий делитель f1(x) и f2(x):
f1(x) = x6 4x5 + 11x4 27x3 + 37x2 35x + 35,
f2(x) = x5 3x4 + 7x3 20x2 + 10x 25.
Ответы .
1а. (x1)(x3 x2 + 3x 3) + 5. 2б. U(x) = 1/2(x2 + 3),
1б. [4x2 (3 + 4i)x 1+ V(x)=1/2(x4 2x2 2).
+ 7i](x + 1 + i) + 8 6i. 3a. х3 + x2 + 2.
2а. U(x) = 1/3(16x2 + 37x + 26), 3б. x2 + x + 1.
V(x) = 1/3(16x3 53x2 4. (x1)3(x+1).
37х + 23). 5. (3 x)f1(x) + (x2 4x +4)f2(x) =
= x2 + 5.
Задание № 114
Разложить на неприводимые множители над полем С или полем
вещественных чисел многочлены:
1. х6 6х4 4х3 + 9х2 + 12х + 4, 2. x4 10х2 + 1,
3. х2n + хn + 1, 4. x4 ах2 + 1, 2 < a <2.
Ответы .
1. (x + 1)4(x 2)2.
2.
(x ![]() )(x
)(x
![]() )(x
+
)(x
+
![]() )(x
+
)(x
+
![]() ).
).
4n1 0 (2k+1)2 7p
3.
![]() x2
2xсos
x2
2xсos![]() + 1).
+ 1).
4.
(x2
x![]() +
1)(x2
+
x
+
1)(x2
+
x![]() + 1).
+ 1).
