Примерные варианты контрольных работ

Контрольная работа №1:

линии 1-го порядка на плоскости

1. Найдите координаты точки Q, симметричной точке P(-5,13), относительно прямой

. 2. Отклонения точки M от прямых и равны соответст- венно –3 и –5. Определите координаты точки M. 3. Найдите уравнение прямой, принадлежащей пучку прямых, проходящих через точку пересечения прямых и и перпендикулярной прямой .

Контрольная работа №2:

линии 2-го порядка на плоскости, аналитическая геометрия в пространстве

1. Составьте уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично

относительно начала координат, если даны точка M(9/2,-1) гиперболы и уравнения её асимптот .

2. Найдите канонические уравнения следующей прямой: 3. Напишите уравнение плоскости, проходящей через точки и , перпендикулярно плоскости .

Контрольная работа №3:

вычисление пределов последовательностей

1. . 2. . 3. . 4. .

Контрольная работа №4:

исследование функций и построение их графиков

1. . 2. . 3. . 4. . 5. . 6. . 7. . 8. .

Контрольная работа №5:

вычисление интегралов.

1. Выполните интегрирование и проверьте дифференцированием: .

2. Найдите площадь фигуры, ограниченной графиком функции и прямыми:

3. Вычислите несобственный интеграл или установите его расходимость: .

Контрольная работа №6:

линейная алгебра и теория матриц.

1. Найдите , если 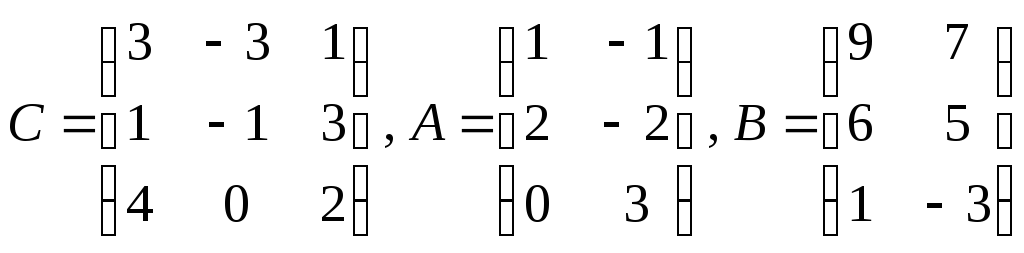. 2. Выясните линейно зависимы или линейно независимы векторы и найдите представление вектора , где . 3. Запишите в общем виде систему линейных уравнений, если заданы матрица системы A и вектор правых частей b: .

Составитель : Васильев А.А.

Перечень базовых определений, понятий, соотношений и алгоритмов действий, которые выпускник должен иметь в оперативной памяти

1. Понятие множества.

2. Декартова система координат на плоскости и в пространстве.

3. Уравнение прямой на плоскости.

4. Функция одной вещественной переменной и ее график.

5. Понятие непрерывной функции.

6. Производная и ее вычисление в простейших случаях.

7. Понятие об определенном и неопределенном интегралах, формула Ньютона-Лейбница.

8. Понятие о системе линейных алгебраических уравнений и методе их решения.

9. Матрицы и простейшие операции над ними.

10. Функция нескольких вещественных переменных, частные производные.

11. Случайное событие, вероятность.

12. Случайная величина, закон ее распределения, математическое ожидание, дисперсия, мода и медиана.

Основные определения, понятия и операции

1. Множество, его элементы, способы задания, операции над множествами.

2. Понятие отображения.

3. Декартова система координат на плоскости и в пространстве. Точки и их координаты.

4. Уравнение прямой на плоскости. Различные формы уравнения прямой.

5. Уравнения окружности, эллипса, гиперболы и параболы.

6. Векторы и операции над ними.

7. Скалярное произведение векторов.

8. Уравнение плоскости.

9. Уравнение прямой в пространстве.

10. Числовые множества на вещественной прямой: отрезок, интервалы и т.д.

11. Инфимум и супремум множества.

12. Числовая последовательность.

13. Предел числовой последовательности.

14. Вычисление пределов в простейших случаях.

15. Монотонные последовательности

16. Число Эйлера (число е).

17. Понятие функции. Способы задания функций. Некоторые важные классы функций: монотонные функции, четные и нечетные функции, периодические функции.

18. Обратная функция, ее график. Нахождение в простейших случаях.

19. Сложная функция, ее анализ и синтез.

20. Предел функции.

21. Простейшие свойства операции предельного перехода.

22. Вычисление пределов функций в простейших случаях.

23. Непрерывность функции в точке и на множестве.

24. Разрывные функции. Точки разрыва и их классификация.

25. Максимумы и минимумы функций непрерывных на отрезке.

26. Понятие производной. Дифференцируемость функции в точке и на отрезке.

27. Производная как наклон касательной и как скорость.

28. Соотношение между непрерывностью и дифференцируемостью функции.

29. Общие правила вычисления производных.

30. Вычисление производной в простейших случаях.

31. Понятие дифференциала и его применение в приближенных вычислениях.

32. Экстремумы функций и их нахождение.

33. Выпуклые и вогнутые функции, точки перегиба.

34. Построение графиков функций в простейших случаях.

35. Понятие определенного интеграла. Интеграл как площадь.

36. Первообразная, неопределенный интеграл.

37. Формула Ньютона-Лейбница.

38. Несобственные интегралы 1-го и 2-го типов.

39. Аналитическое решение системы двух линейных уравнений с двумя неизвестными.

40. Аналитическое решение системы двух линейных уравнений с тремя неизвестными.

41. Метод Гаусса решения системы линейных уравнений общего вида.

42. Понятие матрицы. Элементы матрицы, строки и столбцы матрицы.

43. Частные случаи матриц: вектор-строки и вектор-столбцы, квадратные матрицы, верхняя и нижняя треугольные матрицы, единичная матрица, единичные векторы.

44. Матричные неравенства.

45. Операции над матрицами.

46. Понятие определителя квадратной матрицы.

47. Вычисление определителей в простейших случаях (для матриц небольшой размерности).

48. Ранг матрицы. Вырожденные и невырожденные матрицы.

49. Обратная матрица и ее вычисление с помощью матода Гаусса.

50. Понятие n-мерного векторного пространства.

51. Линейная комбинация n-мерных векторов.

52. Специальные линейные комбинации векторов: неотрицательная и выпуклая.

53. Линейно зависимые и линейно независимые системы векторов.

54. Понятие базиса системы векторов.

55. Базис n-мерного векторного пространства.

56. Представление заданного вектора в фиксированном базисе: вычислительные аспекты.

57. Понятие о функции нескольких вещественных переменных.

58. Частные производные функции нескольких переменных и их вычисление в простейших случаях.

59. Экстремумы функций нескольких переменных.

ЛИТЕРАТУРА по курсу “Высшая математика”