1.1.2 Определение структурного типа активированных углей

М.М. Дубинин и Л.В. Радушкевич разделили в первом приближении активированные угли на три структурных типа [1] в зависимости от так называемого обгара, который является количественной характеристикой степени активирования угля. Обгар находят из отношения количества сгоревшего угля к исходному и выражают в процентах.

Умеренное активирование при достижении обгаров приблизительно до 50% приводит к получению активных углей 1-го структурного типа. При обгаре, большем 75%,получаются активные угли 2-го структурного типа. Области промежуточных обгаров приблизительно от 50 до 75% отвечают активные угли смешанного типа.

Уравнение изотермы адсорбции для любого пара на активном угле 1-го структурного типа имеет вид

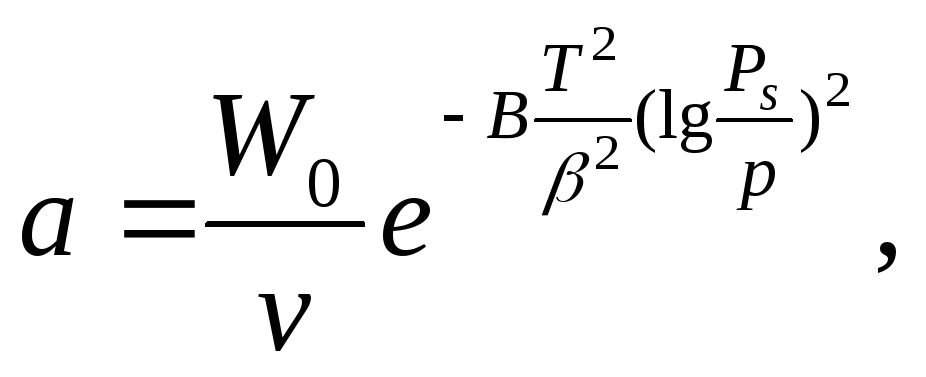(7)

Где - равновесная величина адсорбции при равновесном относительном давлении P/P_s; W₀- предельный объем адсорбционного пространства; v- молярный объем жидкости; B- константа, характеризующая пористую структуру сорбента, которая определяется размером микропор; - коэффициент аффинности; P_s - упругость насыщенного пара при температуре опыта.

Для определения констант W₀ и B по экспериментальным точкам применяют уравнение изотермы адсорбции в линейной форме:

(8)

В котором

Где C- отрезок, отсекаемый прямой на оси ординат; - предельная величина адсорбции;

Представляет собой tg угла наклона прямой к оси абсцисс. Экспериментальные точки, полученные при измерении изотермы адсорбции паров бензола на углях 1-го структурного типа, удовлетворительно ложатся на прямые линии в координатах. Уравнение изотермы адсорбции для углей 1-го структурного типа применимо в широком интервале равновесных относительных давлений от 110^-5 до 0,2. Константа B изменяется в пределах от 0,310^-6 до 1,210^-6, а W₀ – от 0.050 до 0.50 см³/г.

Уравнение изотермы адсорбции для любого пара на активном угле 2-го структурного типа

(9)

Где – предельный объем адсорбционного пространства; A - константа, зависящая от энергетической неоднородности собственно поверхности угля.

Остальные обозначения имеют тот же смысл, что и в уравнении изотермы для углей 1-го структурного типа.

Для нахождения констант и A представляют уравнение изотермы в линейной форме:

(10)

Где и .

По значениям M и N рассчитывают W₀^’ и A. Если опытные данные удовлетворительно укладываются на прямую в координатах, то уравнение (9) применимо для данного случая. Интервал применимости уравнения (9) – от 1,010^-5 до 0,1 P/P_s. Значение коэффициента A колеблется от 1,510^-3 до 2.610^-3.

1.2. Использование расчетного аппарата теории объемного заполнения микропор для обработки

экспериментальной изотермы стандартного пара-бензола на различных углеродных адсорбентах [5]

Основное уравнение теории имеет вид

(11)

Где – безразмерный параметр функции распределения, выражающий степень заполнения микропор ( - предельная величина адсорбции при P/P_s=1; - равновесная величина адсорбции при данном P/P_s); A – дифференциальная максимальная мольная работа адсорбции, равная со знаком минус изменению свободной энергии Гиббса, кал/моль:

(12)

При R=1.98 кал/мольград формула (12) принимает вид

(13)

E – характеристическая свободная энергия адсорбции, кал/моль; n – параметр функции, выражающийся небольшим целым числом (для однородномикропористых структур с очень мелкими микропорами n=3; для углей с разнородной микропористой структурой с не слишком мелкими микропорами n=2).

Уравнение (11) в общем виде выражает распределение заполнения микропор по дифференциальной мольной работе адсорбции A, причем параметры распределения E и n не зависят от температуры, если соблюдается температурная инвариантность характеристических кривых.

Согласно уравнению (11) выражение для характеристической кривой будет иметь вид

(14)

При условии, если для различных паров функция f и параметр n остаются неизменными, то

(15)

т.е. характеристические кривые в координатах являются аффинными ( - коэффициент аффинности, индексом “0” обозначены величины для стандартного пара).

Принимая температурную инвариантность уравнения (11) и известное в математической статистике распределение Вейбула [6], М.М. Дубинин и В.А. Астахов получили термическое уравнение адсорбции в аналитической форме [7]:

(16)

Откуда

(17)

Из уравнения (17) следует, что при =0,368, где e – основание натуральных логарифмов, E=A₀, т.е. характеристическая энергия адсорбции E равна дифференциальной мольной работе адсорбции для данного заполнения =0,368.

При замене получают термическое уравнение адсорбции

(18)

Или в линейной форме.

(19)